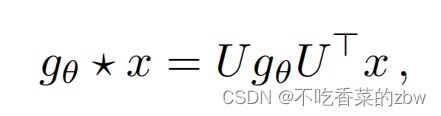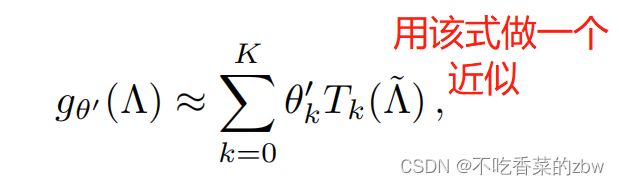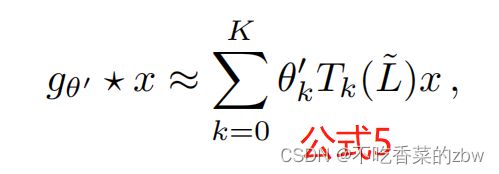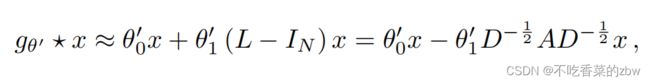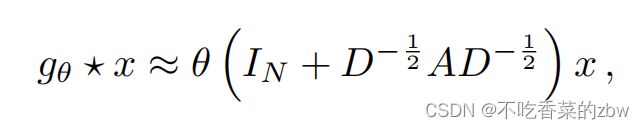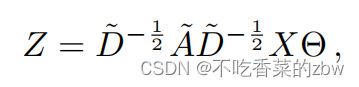论文阅读”Semi-supervised classification with graph convolutional networks“(ICLR2017)
论文标题
Semi-supervised classification with graph convolutional networks
论文作者、链接
作者:
Kipf, Thomas N and Welling, Max
链接:https://arxiv.org/abs/1609.02907
代码:dgl/examples/mxnet/gcn at master · dmlc/dgl · GitHub
Introduction逻辑(论文动机&现有工作存在的问题)
在图中的结点分类的问题中,只有一部分的结点有标签的问题,这个问题可以被框定为基于图的半监督学习,其中标签信息通过某种形式的基于图的显式正则化存在图中,比如,通过在损失函数中使用图的拉普拉斯正则化:
公式1中,![]() 是图中有标签的部分的监督损失,
是图中有标签的部分的监督损失,![]() 为任意神经网络式的函数,
为任意神经网络式的函数,![]() 是权重参数,
是权重参数,![]() 是关于结点特征向量
是关于结点特征向量![]() 的矩阵。
的矩阵。![]() 代表带有
代表带有![]() 个结点
个结点![]() ,已经边
,已经边![]() 的无向图
的无向图![]() 的非归一化图拉普拉斯,及其对应的邻接矩阵
的非归一化图拉普拉斯,及其对应的邻接矩阵![]() 以及一个度矩阵
以及一个度矩阵![]() 。公式1依赖于,图中所有连接的结点都是相似的,并且共享同样的标签。但是这个假设会限制模型的容量,因为图边不一定要编码节点相似度,但可以包含额外的信息。(不知道怎么翻译,原文如下:This assumption, however, might restrict modeling capacity, as graph edges need not necessarily encode node similarity, but could contain additional information.感觉大概意思是对图的边进行编码,会影响模型容量)
。公式1依赖于,图中所有连接的结点都是相似的,并且共享同样的标签。但是这个假设会限制模型的容量,因为图边不一定要编码节点相似度,但可以包含额外的信息。(不知道怎么翻译,原文如下:This assumption, however, might restrict modeling capacity, as graph edges need not necessarily encode node similarity, but could contain additional information.感觉大概意思是对图的边进行编码,会影响模型容量)
本文提出的模型,直接使用一个神经网络![]() 对所有有标签的结点进行训练,在目标
对所有有标签的结点进行训练,在目标![]() 的监督下,因此避免在损失函数中使用具体的基于图的正则化。对图的邻接矩阵进行条件化f(·)将允许模型分配来自监督损失L0的梯度信息,并使其能够学习有标签和无标签节点的表示。根据图的邻接矩阵对
的监督下,因此避免在损失函数中使用具体的基于图的正则化。对图的邻接矩阵进行条件化f(·)将允许模型分配来自监督损失L0的梯度信息,并使其能够学习有标签和无标签节点的表示。根据图的邻接矩阵对![]() 进行调整,会使得模型从从监督损失
进行调整,会使得模型从从监督损失![]() 中分配梯度信息,使其拥在没有标签的情况下学习结点特征的能力。
中分配梯度信息,使其拥在没有标签的情况下学习结点特征的能力。
论文核心创新点
1. 引入了一个简单且有效的,针对神经网络模型的逐层传播规则,该规则直接在图上操作,并且展示如何从谱图卷积的一阶近似得到它。
2. 证明了这种基于图的神经网络如何能够使用在结点的半监督分类任务上
论文方法
图上的快速近似卷积
本节提供图神经网络的理论动机。
先考虑一个多层的图卷积网络(Graph Convolutional Network ,GCN),以如下的逐层传播公式:
其中,![]() 是无向图
是无向图![]() 的自链接的(self-connections)邻接矩阵。
的自链接的(self-connections)邻接矩阵。![]() 是单位矩阵,
是单位矩阵,![]() ,
,![]() 是一个特定层的可训练权重矩阵。
是一个特定层的可训练权重矩阵。![]() 是激活函数,比如
是激活函数,比如![]() 。
。![]() 是第
是第![]() 层的激活后的矩阵,
层的激活后的矩阵,![]() 。接下来证明了这种传播规则的形式,可以通过图上局部谱滤波器的一阶近似来激发。
。接下来证明了这种传播规则的形式,可以通过图上局部谱滤波器的一阶近似来激发。
特别的图卷积
考虑在图上的特别卷积,在傅里叶域中,一个信号![]() 和由参数
和由参数![]() 控制的滤波器
控制的滤波器![]() ,即:
,即:
其中![]() 是归一化图拉普拉斯特征向量
是归一化图拉普拉斯特征向量![]() 的矩阵,带一个特征向量的对角矩阵
的矩阵,带一个特征向量的对角矩阵![]() 以及
以及![]() 是对x经过傅里叶变换得到的图。
是对x经过傅里叶变换得到的图。![]() 可以理解为是对于矩阵
可以理解为是对于矩阵![]() 的特征值的函数,即,
的特征值的函数,即,![]() 。上述式子的计算复杂度是
。上述式子的计算复杂度是![]() ,并且计算大型图的拉普拉斯矩阵也是特别消耗算力的。于是作者使用切比雪夫多项式(Chebyshev polynomials)
,并且计算大型图的拉普拉斯矩阵也是特别消耗算力的。于是作者使用切比雪夫多项式(Chebyshev polynomials)![]() 的K阶对
的K阶对![]() 做近似计算:
做近似计算:
以及对矩阵![]() 进行变换
进行变换![]() 。
。![]() 代表矩阵
代表矩阵![]() 中最大的向量。
中最大的向量。![]() 是切比雪夫系数的向量。切比雪夫多项式递归定义为
是切比雪夫系数的向量。切比雪夫多项式递归定义为![]() ,其中
,其中![]() 。
。
回到对于带滤波器![]() 的信号
的信号![]() 的定义,现在有:
的定义,现在有:
其中![]() 。易证得
。易证得![]() 。注意,这个表达式现在是
。注意,这个表达式现在是![]() 定域的,因为它是拉普拉斯多项式中的
定域的,因为它是拉普拉斯多项式中的![]() 阶多项式,即,该式现在只依赖于距离中心节点最大
阶多项式,即,该式现在只依赖于距离中心节点最大![]() 步的节点(第
步的节点(第![]() 个顺序的邻居点)。
个顺序的邻居点)。
逐层线性模型
一个基于图卷积的神经网络,通过堆叠多个卷积层构成,卷积层的卷积公式为公式5,每一层都是逐点非线性的计算。现在,想象我们将分层卷积操作限制为![]() (见公式 5),即一个关于
(见公式 5),即一个关于![]() 线性的函数,因此该卷积是拉普拉斯谱图上的一个线性函数。
线性的函数,因此该卷积是拉普拉斯谱图上的一个线性函数。
至此,我们可以通过堆叠多个这样的卷积层,恢复丰富的卷积滤波器函数类,但是仍然会收到切比雪夫多项式的参数限制。直觉上希望这样一个模型可以减轻在带有宽结点分布的图的局部邻域结构上的过拟合问题。此外,对于固定的计算预算,这种分层的线性公式允许我们构建更深入的模型,这种实践已知可以提高许多领域的建模能力。
在GCN的线性公式中,我们进一步做一个近似,令![]() ,可以预见的是,神经网络参数将在训练过程中适应这种规模的变化。在这种近似下,公式5简化为:
,可以预见的是,神经网络参数将在训练过程中适应这种规模的变化。在这种近似下,公式5简化为:
其中,![]() 是自由参数。该滤波器的参数在整个图中共享。 连续应用这种形式的滤波器可以有效地卷积一个节点的k阶邻域,其中k为神经网络模型中连续滤波操作数目或卷积层数。
是自由参数。该滤波器的参数在整个图中共享。 连续应用这种形式的滤波器可以有效地卷积一个节点的k阶邻域,其中k为神经网络模型中连续滤波操作数目或卷积层数。
在实践中,进一步限制参数的数量以解决过拟合问题和减少每层操作(如矩阵乘法)的数量是有益的。这就得到了下面的表达式:
其中,![]() 。注意
。注意![]() 现在的取值范围是
现在的取值范围是![]() 。因此,在深度神经网络模型中重复使用该算子会导致数值不稳定和爆发/消失的梯度。为了减轻这个问题,作者引入如下的正则化技巧:
。因此,在深度神经网络模型中重复使用该算子会导致数值不稳定和爆发/消失的梯度。为了减轻这个问题,作者引入如下的正则化技巧:![]() ,其中,
,其中,![]() 。
。
可以将这个定义推广到一个带有![]() 个输入通道的信号
个输入通道的信号![]() 和
和![]() 滤波器或特征映射如下:
滤波器或特征映射如下:
其中![]() 是一个滤波器参数矩阵,
是一个滤波器参数矩阵,![]() 是卷积信号矩阵。
是卷积信号矩阵。
半监督结点分类
在介绍了一个简单而灵活的图上信息传播模型![]() 之后,我们可以回到半监督节点分类的问题上。正如在引言中所概述的,我们可以放松通常在基于图的半监督学习中所做的某些假设,通过使我们的模型
之后,我们可以回到半监督节点分类的问题上。正如在引言中所概述的,我们可以放松通常在基于图的半监督学习中所做的某些假设,通过使我们的模型![]() 既适用于数据
既适用于数据![]() ,也适用于底层图结构的邻接矩阵
,也适用于底层图结构的邻接矩阵![]() 。作者希望在邻接矩阵包含数据
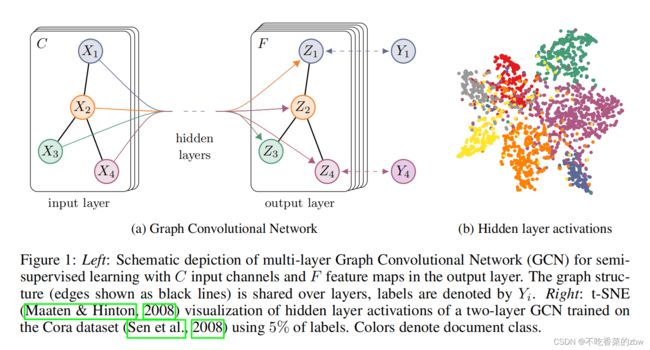
。作者希望在邻接矩阵包含数据![]() 所没有的信息的情况下,这些设定是有用的。模型图如下:
所没有的信息的情况下,这些设定是有用的。模型图如下:
例子
接下来,考虑一个两层的GCN模型,任务是在图上的半监督的结点分类,带有一个对称的邻接矩阵![]() (01式二进制或者是加权的)。在预处理阶段计算
(01式二进制或者是加权的)。在预处理阶段计算![]() 。然后本文的前馈模型以如下公式传播:
。然后本文的前馈模型以如下公式传播:
![]()
其中,![]() 是一个是具有
是一个是具有![]() 个特征映射的隐藏层的输入-隐藏(input-to-hidden)权重矩阵。
个特征映射的隐藏层的输入-隐藏(input-to-hidden)权重矩阵。![]() 是一个隐藏-输出(hidden-to-output)的权重矩阵。softmax激活函数定义为:
是一个隐藏-输出(hidden-to-output)的权重矩阵。softmax激活函数定义为:![]() 其中
其中![]() 。最后对有监督的部分,损失用交叉熵来衡量:
。最后对有监督的部分,损失用交叉熵来衡量:
其中![]() 是有标签的结点编号。
是有标签的结点编号。
神经网络的权重![]() 用梯度下降进行训练。在这项工作中,作者对每个训练迭代使用完整的数据集执行批处理梯度下降,只要数据集适合内存就可以实现。使用
用梯度下降进行训练。在这项工作中,作者对每个训练迭代使用完整的数据集执行批处理梯度下降,只要数据集适合内存就可以实现。使用![]() 的稀疏表示,内存要求变成
的稀疏表示,内存要求变成![]() ,即边edge的数量。通过dropout引入训练过程中的随机性。
,即边edge的数量。通过dropout引入训练过程中的随机性。