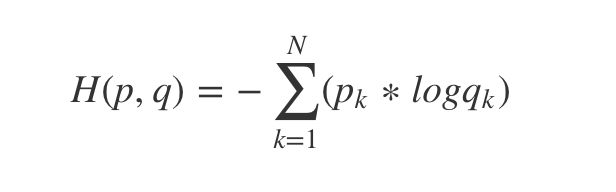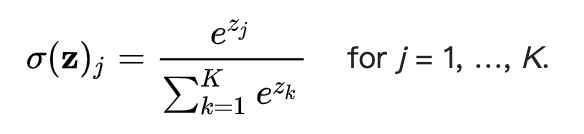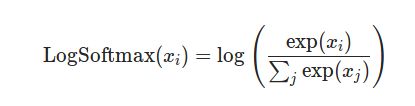pytorch中交叉熵nn.BCELoss与nn.CrossEntropyLoss的区别

参考：https://www.jb51.net/article/181634.htm

简单总结

nn.BCELoss

用于二分类问题，前面应该加一个Sigmoid函数（如下）


当S(x)=0.5，它的斜率是最大，则在x=0时取得最大斜率

nn.CrossEntropyLoss :自动在前面有Sofrmax层

参考：https://blog.csdn.net/watermelon1123/article/details/91044856，
https://blog.csdn.net/liangjiu2009/article/details/107769512（计算过程）
计算

import os
import math
import torch
import torch.nn as nn

criterion = nn.CrossEntropyLoss().cuda()
y_pred = torch.tensor([[ 5.0060,  1.3594, -0.4604,  0.3486,  0.3273,  0.7445,  0.7974, -0.6486,
         -0.5508, -0.6279,  2.7097,  1.7399,  1.4096,  1.0342,  1.4090,  0.5836,
          0.7386,  0.6439,  0.2210,  1.4657, -0.8205, -0.2882, -1.3240,  0.1541,
         -0.2943, -1.2346, -0.3386, -0.2060, -0.6794, -0.8053,  0.0475, -1.6140,
         -1.5633, -1.5470, -1.3992, -1.3593, -1.5412, -1.2203]],
       device='cuda:0',)

l = torch.tensor([0], device='cuda:0')

logsoftmax = nn.LogSoftmax(dim=1)

lsm_a = logsoftmax(y_pred )
# print(logsoftmax(y_pred[j]))
nll = nn.NLLLoss()
ce = nll(lsm_a, l)
print('ce::', ce)
loss = criterion(y_pred, l)
print(loss)

pytorch中使用的交叉熵公式如下

1、而实际计算，先整个计算过程如参考链接中所示，下面是将输出进行softmax后的结果

2、对softmax的结果进行log和取反

对公式最后变形的理解

上面图片的公式算是简化之后的，对于交叉熵的预测结果使用one-hot编码方式，例如，预测输入的东西是三类中的哪一个，标签中会只有一个是1，其他都是0，例如三类预测分别是猫、狗、兔，若这是狗想预测为狗则标签为[0,1,0],但在函数中只要写（假设是一个单通道的图片，）,红色框中表示预测值中和输出标签为1相同索引位置的值，交叉熵最后和这个值相等，因为不是只有一个位置是1标签，其他都是0，累加过程中无用，

criterion = nn.CrossEntropyLoss().cuda()
 # 这个标签的1表示值是1的索引，相当于上面例子中[0,1,0]
loss = criterion(y_pred, [1]) 

如下图中