语音信号线性预测分析

语音信号线性预测分析

基本思想：一个语音取样的现在值可以用若干个语音取样过去值的加权线性组合来逼近（最小均方误差）。线性预测最重要的优势在于它可以较为精确地估计语音的参数，而这些极少的参数可以正确地表现语音信号的时域和频域特性。

基本原理：线性预测分析的基本原理是把信号用一个模型来表示，即将信号看作某一个模型的输出，这样就可以用该模型的参数来描述信号。

数学公式：
$$x(n)=\sum _{i=1}^p{a}_{i}x(n-i)+e(n)$$
x(n)为真实信号，加权项为预测信号，e(n)为预测误差。根据e(n)的最小均方误差准则来计算滤波器系数ai。
$$e(n)=x(n)-\sum _{i=1}^p{a}_{i}x(n-i)$$

$$E=\sum _n{e}^2(n)=\sum _n[x(n)-\sum _{i=1}^p{a}_{i}x(n-i){]}^2$$

为使预测的最小均方误差E最小，对ai求偏导等0：
$$\frac{\partial E}{\partial a_j}=0(1\le j\le p)$$
最小误差结果为：
$$\sum _{n}x(n)x(n-j)=\sum _{i=1}^p{a}_i\sum _{n}x(n-i)x(n-j)$$

$$E=\sum _n[x(n){]}^2-\sum _{i=1}^p{a}_i\sum _{n}x(n)x(n-i)$$

通过自相关解法来求解线性预测系数（Yule-Walker方程），根据加窗自相关函数定义，以及最小误差结果可得：
$$R(j)=-\sum _{i=1}^p{a}_{i}R(j-i)1\le j\le p$$
最小均方误差可写为：
$$E=R(0)+\sum _{i=1}^p{a}_{i}R(i)$$
利用Toeplitz矩阵的性质进行计算，基本思想是递归方法求解，采用Levinson-Durbin算法。

算法过程与步骤：

当i=0时，E0=R(0)，a0=1；

对于第i次递归(i=1,2,…,p):
$$k_i=\frac{1}{E_{i-1}}\left[R(i)-\sum _{j=1}^{i-1}{a}_j^{i-1}R(j-i)\right]$$

$$i{a}_i^{(i)}=k_i$$

$$a_j^{(i)}=a_j^{(i-1)}-k_i{a}_{i-j}^{(i-1)}$$

$$E_i=(1-k_i^2)E_{i-1}$$

最终解为：
$$a_i=a_j^{(p)}1\le j\le p$$

$$E_p=R(0)\prod _{i=1}^p(1-k_i^2)$$

由上式可知，最小均方误差Ep一定大于0，且随着预测器阶数的增加而减少。参数ki一定满足
$$\left|k_i\right|<1,1\le i\le p$$
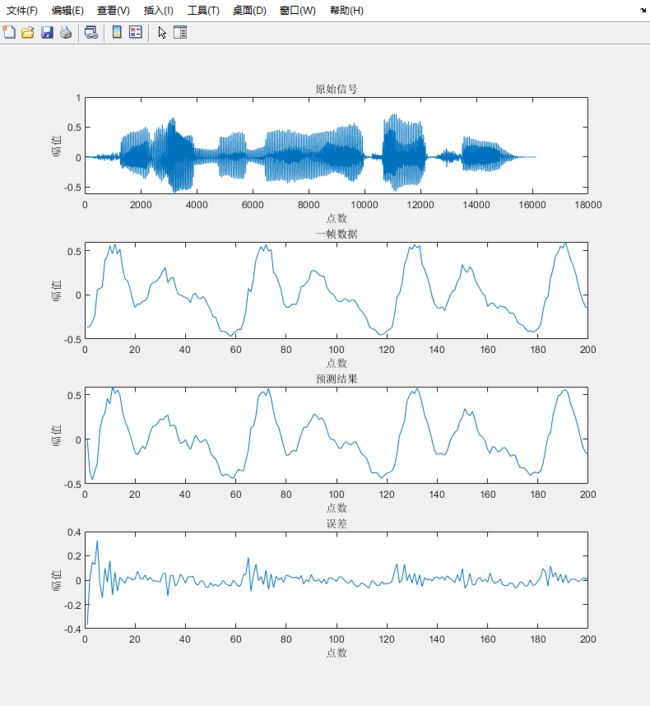
MATLAB工具箱中有lpc函数，使用Levinson-Durbin的自相关方法计算预测系数的。输入一帧的数据以及线性预测阶数，输出预测系数ar和预测误差的方差r。
对一帧语音信号进行实验，预测结果以及误差：

根据Levinson-Durbin自相关法求线性预测系数的原理，编写函数，并于lpc函数进行比较，结果一致。

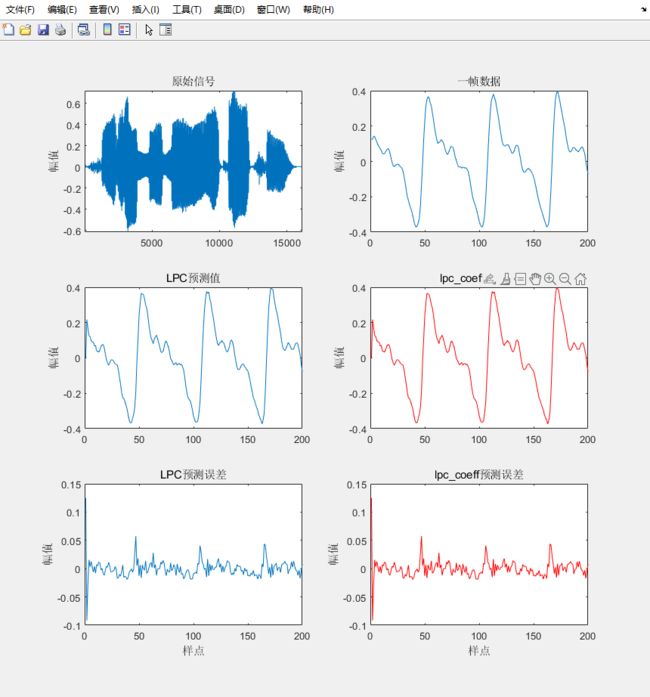
一帧信号的FFT频谱与LPC预测系数的复频谱比较：

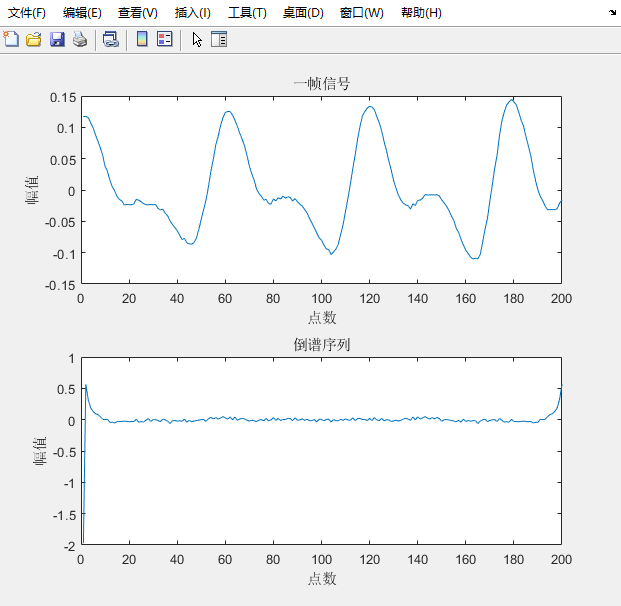
倒谱分析

倒谱（Cepstrum）是表示一帧语音数据特征的一个序列。可以看作和自相关序列类似的东西，也可以理解为自相关序列的对数压缩，因为其携带有和自相关序列类似的信息。信号的倒谱是通过对信号进行离散傅里叶变换，绝对值取平方得到信号的功率谱，然后取对数再做逆离散傅里叶变换得到信号的倒谱。

通过对信号x(n)取离散傅里叶变换，可以得到信号的复数谱：
$$DFT(x(n))\to X(k)$$
通过对复数谱的绝对值取平方得到信号的功率谱：
$${\left|X(k)\right|}^2\to P(k)$$
对功率谱取对数，再做逆离散傅里叶变换
$$IDFT(log(P(k)))\to C(n)$$
一段话一帧倒谱实验：

声母a一帧的倒谱实验：

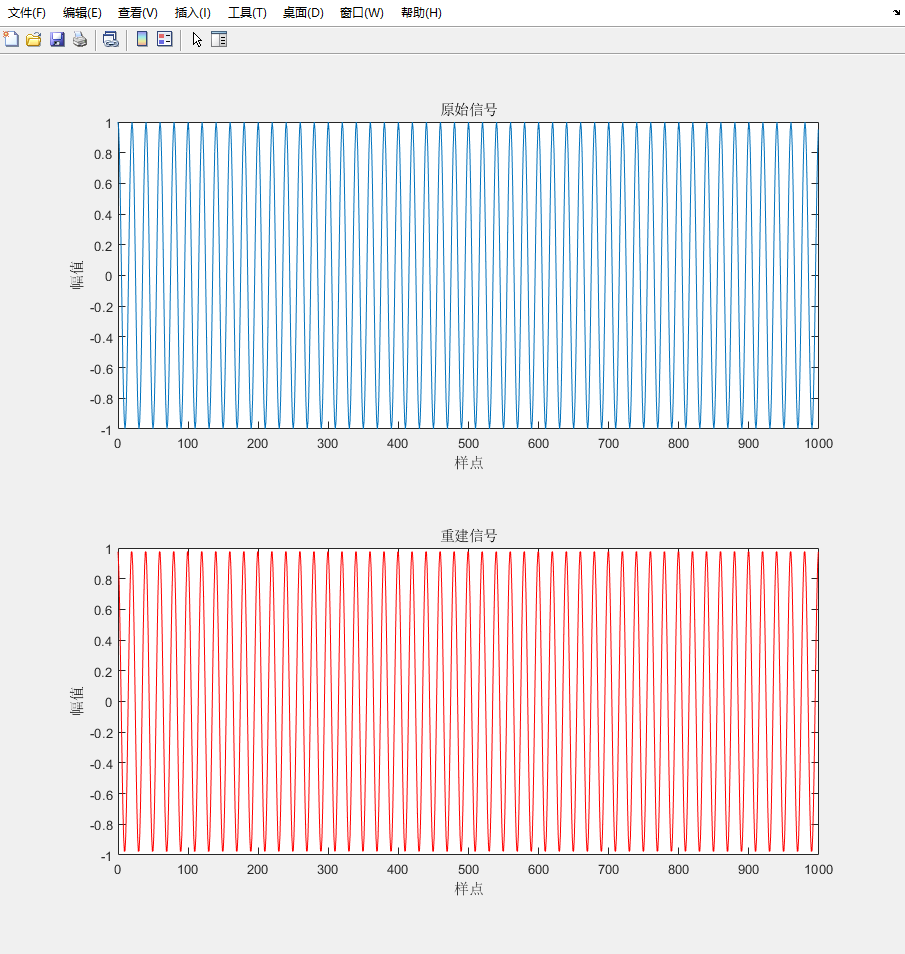
离散余弦变换

离散余弦变换DCT具有信号谱分量丰富，能量集中的特点。对于那些不重要的频域区域和系数就能够直接裁剪掉，因此，DCT变换非常适合于压缩算法的处理。

数学公式：设x(n)是N个有限值的一维实数信号序列，n=0,1,…,N-1，C(k)是正交因子。
$$X(k)=\sqrt{\frac{2}{N}}\sum _{n=0}^{N-1}C(k)x(n)cos\left(\frac{(2n+1)k\pi }{2N}\right)k=0,1,\cdots ,N-1$$

$$C(k)=\{\begin{array}{l}\sqrt{2}/2,k=0\\ 1,k\in [1,N-1]\end{array}$$

调用DCT函数求序列x(n)的DCT系数，然后仅用幅值大于5的系数进行信号重建，比较差异。
$$x(n)=\cos (2\pi fn/f_s)n\in [0,1000],f_s=1000Hz,f=50Hz$$
实验结果：

代码：

%lpc预测结果实验
clear
clc
[x,fs] = audioread('CHMMWJQ.wav');
sound(x,fs);
n = 200; 
xx = enframe(x, n);
m = 60;
y = x((m-1)*n+1:m*n);
p = 12;
ar = lpc(y,p);
est_x = filter([0 -ar(2:end )],1,y);
err = y - est_x;
subplot(411);plot(x);title('原始信号');xlabel('点数');ylabel('幅值');
subplot(412);plot(y);title('一帧数据');xlabel('点数');ylabel('幅值');
subplot(413);plot(est_x);title('预测结果');xlabel('点数');ylabel('幅值');
subplot(414);plot(err);title('差值');xlabel('点数');ylabel('幅值');

%用自相关法求信号s使均方预测误差为最小的预测系数的函数
function [ar,G]=lpc_coeff(s,p)
%算法为Durbin快速递推算法
n=length(s);                                    % 获得信号长度                    
for i=1:p
    Rp(i)=sum(s(i+1:n).*s(1:n-i)); % 计算自相关函数
end
Rp_0=s'*s;      % 即Rn(0)
Ep=zeros(p,1);  % Ep为p阶最佳线性预测反滤波能量
k=zeros(p,1);   % k为偏相关系数
a=zeros(p,p);   % 以上为初始化
%i=1的情况需要特殊处理,也是对p=1进行处理
Ep_0=Rp_0;
k(1)=Rp(1)/Rp_0;
a(1,1)=k(1);
Ep(1)=(1-k(1)^2)*Ep_0;
%i=2起使用递归算法
if p>1
    for i=2:p
        k(i)=(Rp(i)-sum( a(1:i-1,i-1).*Rp(i-1:-1:1)'))/Ep(i-1);
        a(i,i)=k(i);
        Ep(i)=(1-k(i)^2)*Ep(i-1);
        for j=1:i-1
            a(j,i)=a(j,i-1)-k(i)*a(i-j,i-1);
        end
    end
end
ar=a(:,p);
ar=[1 -1*ar'];
G=sqrt(Ep(p));

%线性预测系数对比
clear all; clc; close all;
[x,fs]=wavread('CHMMWJQ.wav');
L=200;
y=x(8001:8000+L);
p=12; 
ar1=lpc(y,p);
ar2=lpc_coeff(y,p); 
est_x1=filter([0 -ar1(2:end)],1,y); 
est_x2=filter([0 -ar2(2:end)],1,y); 
err1=y-est_x1; 
err2=y-est_x2; 
subplot 321; plot(x); axis tight;title('原始信号'); ylabel('幅值')
subplot 322; plot(y); xlim([0 L]); title('一帧数据'); ylabel('幅值')
subplot 323; plot(est_x1); xlim([0 L]); title('LPC预测值'); ylabel('幅值')
subplot 324; plot(est_x2,'r'); xlim([0 L]); title('lpc\_coeff预测值'); ylabel('幅值')
subplot 325; plot(err1); xlim([0 L]); title('LPC预测误差'); ylabel('幅值'); xlabel('样点')
subplot 326; plot(err2,'r'); xlim([0 L]); title('lpc\_coeff预测误差'); ylabel('幅值'); xlabel('样点')

%比较LPC预测系数的复频谱与FFT频谱
clear all; clc; close all;
[x,fs]=wavread('CHMMWJQ.wav');
L=200;     
p=12; 
y=x(8001:8000+L); 
ar=lpc(y,p); 
nfft=512;
W2=nfft/2;
m=1:W2+1;
Y=fft(y,nfft); 
ff=(fft(ar.',2*W2+2).').^(-1);
Y1=ff(1:length(ff)/2); 
% 作图
subplot 211; plot(y);title('一帧语音信号的波形'); ylabel('幅值'); xlabel('(a)')
subplot 212; plot(m,20*log10(abs(Y(m))));axis([0 200 -inf inf]);
hold on;
plot(m,20*log10(abs(Y1)),'color','r');axis([0 200 -inf inf]); 
ylabel('幅值/db');legend('FFT频谱','LPC复频谱'); xlabel('样点');title('FFT频谱和LPC谱的比较');

%倒谱计算
clear
clc
[x,fs]=audioread('CHMMWJQ.wav');
len=200;
% nfft=128;
y=x(6001:6000+len);
Xk=fft(y);
Pk=(abs(Xk));
Cn=ifft(log(Pk));
[xh,yh]=rceps(y);
subplot(211);plot(y);xlabel('点数');ylabel('幅值');title('一帧信号');
subplot(212);plot(Cn);xlabel('点数');ylabel('幅值');title('倒谱序列');

%DCT变换
clear
clc
f=50;
fs=1000;
N=1000;
n=(0:N-1);
xn=cos(2*pi*f*n/fs);
xd=dct(xn);
zn=xd;
num=find(abs(xd)<5);
xd(num)=0;
y=idct(xd);
subplot 211;plot(n,xn);title('原始信号');xlabel('样点');ylabel('幅值');
subplot 212;plot(n,y,'r');title('重建信号');xlabel('样点');ylabel('幅值');

%DCT变换
clear
clc
f=50;
fs=1000;
N=1000;
n=(0:N-1);
xn=cos(2*pi*f*n/fs);
xd=dct(xn);
zn=xd;
num=find(abs(xd)<5);
xd(num)=0;
y=idct(xd);
subplot 211;plot(n,xn);title('原始信号');xlabel('样点');ylabel('幅值');
subplot 212;plot(n,y,'r');title('重建信号');xlabel('样点');ylabel('幅值');