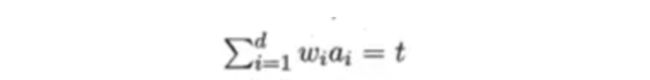详解决策树 Decision Tree

详解决策树 Decision Tree

基本概念

定义：
决策树是一种自上而下 ，对样本数据进行树形分类的过程，由结点和有向边组成 。结点分为内部结点和叶结点，其中每个内部结点表示一个特征或属性，叶结点表示类别 。从顶部根结点开始，所有样本聚在一起 。经过根结点的划分 ，样本被分到不同的子结点中 。 再根据子结点的特征进一步划分，直至所有样本都被归到某一个类别(即叶结点)中 。

结构：
显然，决策树在逻辑上以树的形式存在，包含根节点、内部结点和叶节点。

• 根节点：包含数据集中的所有数据的集合
• 内部节点：每个内部节点为一个判断条件，并且包含数据集中满足从根节点到该节点所有条件的数据的集合。根据内部结点的判断条件测试结果，内部节点对应的数据的集合别分到两个或多个子节点中。
• 叶节点：叶节点为最终的类别，被包含在该叶节点的数据属于该类别。

特征选择

决策树学习的关键在于如何选择划分属性，不同的划分属性得出不同的分支结构，从而影响整颗决策树的性能。属性划分的目标是让各个划分出来的子节点尽可能地“纯”，即属于同一类别。因此下面便是介绍量化纯度的具体方法：
信息增益（ID3）信息增益率（C4.5）基尼指数(CART)

信息增益

信息熵

先对一个节点的纯度进行定义，我们将其称之为信息熵：


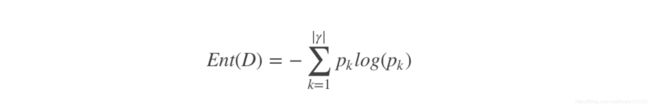
由定义可知，熵只依赖于X的分布，而与X的取值无关。

信息熵的特点：

信息增益

由此，我们得到了一种选择划分属性的方法，计算以每个属性进行划分子节点得到的信息增益，选择其中最大的作为选择的属性。

ID3 算法

算法流程

Python实现源码

# -*- coding: utf-8 -*-
from math import log
import operator
import tree_plotter
def create_data_set():
    """
    创建样本数据
    :return:
    """
    data_set = [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
    labels = ['no surfacing', 'flippers']
    return data_set, labels
def calc_shannon_ent(data_set):
    """
    计算信息熵
    :param data_set: 如： [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
    :return:
    """
    num = len(data_set)  # n rows
    # 为所有的分类类目创建字典
    label_counts = {}
    for feat_vec in data_set:
        current_label = feat_vec[-1]  # 取得最后一列数据
        if current_label not in label_counts.keys():
            label_counts[current_label] = 0
        label_counts[current_label] += 1
    # 计算香浓熵
    shannon_ent = 0.0
    for key in label_counts:
        prob = float(label_counts[key]) / num
        shannon_ent = shannon_ent - prob * log(prob, 2)
    return shannon_ent
def split_data_set(data_set, axis, value):
    """
    返回特征值等于value的子数据集，切该数据集不包含列（特征）axis
    :param data_set:  待划分的数据集
    :param axis: 特征索引
    :param value: 分类值
    :return:
    """
    ret_data_set = []
    for feat_vec in data_set:
        if feat_vec[axis] == value:
            reduce_feat_vec = feat_vec[:axis]
            reduce_feat_vec.extend(feat_vec[axis + 1:])
            ret_data_set.append(reduce_feat_vec)
    return ret_data_set
def choose_best_feature_to_split(data_set):
    """
    按照最大信息增益划分数据
    :param data_set: 样本数据，如： [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
    :return:
    """
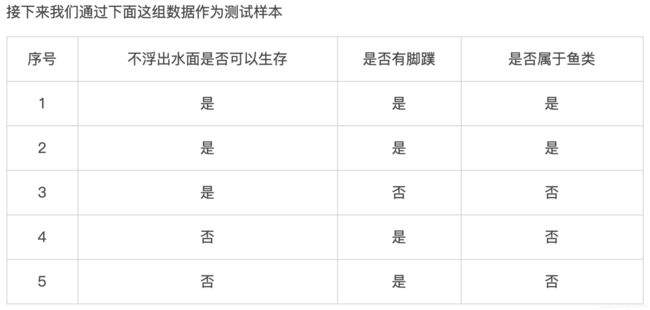
    num_feature = len(data_set[0]) - 1 # 特征个数，如：不浮出水面是否可以生存  和是否有脚蹼
    base_entropy = calc_shannon_ent(data_set) # 经验熵H(D)
    best_info_gain = 0
    best_feature_idx = -1
    for feature_idx in range(num_feature):
        feature_val_list = [number[feature_idx] for number in data_set]  # 得到某个特征下所有值（某列）
        unique_feature_val_list = set(feature_val_list)  # 获取无重复的属性特征值
        new_entropy = 0
        for feature_val in unique_feature_val_list:
            sub_data_set = split_data_set(data_set, feature_idx, feature_val)
            prob = len(sub_data_set) / float(len(data_set)) # 即p(t)
            new_entropy += prob * calc_shannon_ent(sub_data_set) #对各子集香农熵求和
        info_gain = base_entropy - new_entropy # 计算信息增益，g(D,A)=H(D)-H(D|A)
        # 最大信息增益
        if info_gain > best_info_gain:
            best_info_gain = info_gain
            best_feature_idx = feature_idx
    return best_feature_idx
def majority_cnt(class_list):
    """
    统计每个类别出现的次数，并按大到小排序，返回出现次数最大的类别标签
    :param class_list: 类数组
    :return:
    """
    class_count = {}
    for vote in class_list:
        if vote not in class_count.keys():
            class_count[vote] = 0
        class_count[vote] += 1
    sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reversed=True)
    print sorted_class_count[0][0]
    return sorted_class_count[0][0]
def create_tree(data_set, labels):
    """
    构建决策树
    :param data_set: 数据集合，如： [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
    :param labels: 标签数组，如：['no surfacing', 'flippers']
    :return:
    """
    class_list = [sample[-1] for sample in data_set] # ['yes', 'yes', 'no', 'no', 'no']
    # 类别相同，停止划分
    if class_list.count(class_list[-1]) == len(class_list):
        return class_list[-1]
    # 长度为1，返回出现次数最多的类别
    if len(class_list[0]) == 1:
        return majority_cnt((class_list))
    # 按照信息增益最高选取分类特征属性
    best_feature_idx = choose_best_feature_to_split(data_set)  # 返回分类的特征的数组索引
    best_feat_label = labels[best_feature_idx]  # 该特征的label
    my_tree = {best_feat_label: {}}  # 构建树的字典
    del (labels[best_feature_idx])  # 从labels的list中删除该label，相当于待划分的子标签集
    feature_values = [example[best_feature_idx] for example in data_set]
    unique_feature_values = set(feature_values)
    for feature_value in unique_feature_values:
        sub_labels = labels[:]  # 子集合
        # 构建数据的子集合，并进行递归
        sub_data_set = split_data_set(data_set, best_feature_idx, feature_value) # 待划分的子数据集
        my_tree[best_feat_label][feature_value] = create_tree(sub_data_set, sub_labels)
    return my_tree
def classify(input_tree, feat_labels, test_vec):
    """
    决策树分类
    :param input_tree: 决策树
    :param feat_labels: 特征标签
    :param test_vec: 测试的数据
    :return:
    """
    first_str = list(input_tree.keys())[0]  # 获取树的第一特征属性
    second_dict = input_tree[first_str]  # 树的分子，子集合Dict
    feat_index = feat_labels.index(first_str)  # 获取决策树第一层在feat_labels中的位置
    for key in second_dict.keys():
        if test_vec[feat_index] == key:
            if type(second_dict[key]).__name__ == 'dict':
                class_label = classify(second_dict[key], feat_labels, test_vec)
            else:
                class_label = second_dict[key]
            return class_label
data_set, labels = create_data_set()
decision_tree = create_tree(data_set, labels)
print "决策树：", decision_tree
data_set, labels = create_data_set()
print "（1）不浮出水面可以生存，无脚蹼：", classify(decision_tree, labels, [1, 0])
print "（2）不浮出水面可以生存，有脚蹼：", classify(decision_tree, labels, [1, 1])
print "（3）不浮出水面可以不能生存，无脚蹼：", classify(decision_tree, labels, [0, 0])

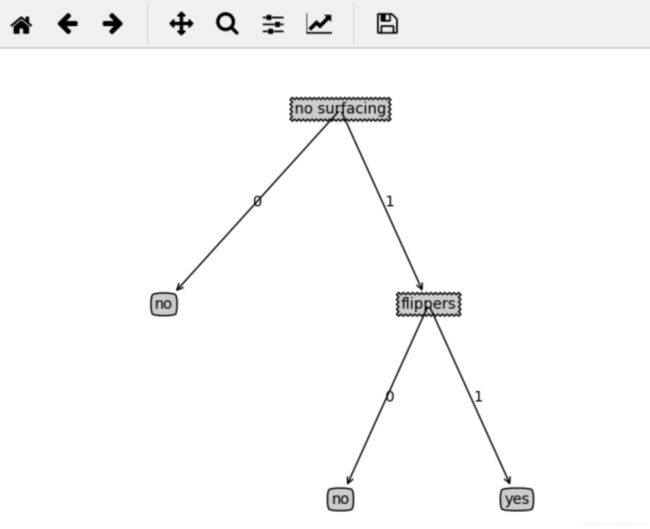
tree_plotter.create_plot(decision_tree)

画图程序，tree_plotter.py：

import matplotlib.pyplot as plt
decision_node = dict(boxstyle="sawtooth", fc="0.8")
leaf_node = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
def plot_node(node_txt, center_pt, parent_pt, node_type):
    create_plot.ax1.annotate(node_txt, xy=parent_pt, xycoords='axes fraction', \
                             xytext=center_pt, textcoords='axes fraction', \
                             va="center", ha="center", bbox=node_type, arrowprops=arrow_args)
def get_num_leafs(my_tree):
    num_leafs = 0
    first_str = list(my_tree.keys())[0]
    second_dict = my_tree[first_str]
    for key in second_dict.keys():
        if type(second_dict[key]).__name__ == 'dict':
            num_leafs += get_num_leafs(second_dict[key])
        else:
            num_leafs += 1
    return num_leafs
def get_tree_depth(my_tree):
    max_depth = 0
    first_str = list(my_tree.keys())[0]
    second_dict = my_tree[first_str]
    for key in second_dict.keys():
        if type(second_dict[key]).__name__ == 'dict':
            thisDepth = get_tree_depth(second_dict[key]) + 1
        else:
            thisDepth = 1
        if thisDepth > max_depth:
            max_depth = thisDepth
    return max_depth
def plot_mid_text(cntr_pt, parent_pt, txt_string):
    x_mid = (parent_pt[0] - cntr_pt[0]) / 2.0 + cntr_pt[0]
    y_mid = (parent_pt[1] - cntr_pt[1]) / 2.0 + cntr_pt[1]
    create_plot.ax1.text(x_mid, y_mid, txt_string)
def plot_tree(my_tree, parent_pt, node_txt):
    num_leafs = get_num_leafs(my_tree)
    depth = get_tree_depth(my_tree)
    first_str = list(my_tree.keys())[0]
    cntr_pt = (plot_tree.x_off + (1.0 + float(num_leafs)) / 2.0 / plot_tree.total_w, plot_tree.y_off)
    plot_mid_text(cntr_pt, parent_pt, node_txt)
    plot_node(first_str, cntr_pt, parent_pt, decision_node)
    second_dict = my_tree[first_str]
    plot_tree.y_off = plot_tree.y_off - 1.0 / plot_tree.total_d
    for key in second_dict.keys():
        if type(second_dict[key]).__name__ == 'dict':
            plot_tree(second_dict[key], cntr_pt, str(key))
        else:
            plot_tree.x_off = plot_tree.x_off + 1.0 / plot_tree.total_w
            plot_node(second_dict[key], (plot_tree.x_off, plot_tree.y_off), cntr_pt, leaf_node)
            plot_mid_text((plot_tree.x_off, plot_tree.y_off), cntr_pt, str(key))
    plot_tree.y_off = plot_tree.y_off + 1.0 / plot_tree.total_d
def create_plot(in_tree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    create_plot.ax1 = plt.subplot(111, frameon=False, **axprops)
    plot_tree.total_w = float(get_num_leafs(in_tree))
    plot_tree.total_d = float(get_tree_depth(in_tree))
    plot_tree.x_off = -0.5 / plot_tree.total_w
    plot_tree.y_off = 1.0
    plot_tree(in_tree, (0.5, 1.0), '')
    plt.show()

输出结果
决策树： {‘no surfacing’: {0: ‘no’, 1: {‘flippers’: {0: ‘no’, 1: ‘yes’}}}}
（1）不浮出水面可以生存，无脚蹼： no
（2）不浮出水面可以生存，有脚蹼： yes
（3）不浮出水面可以不能生存，无脚蹼： no

作图结果

信息增益率

信息增益的不足

信息增益原则对于每个分支节点，都会乘以其权重，也就是说，由于权重之和为1，所以分支节点分的越多，即每个节点数据越小，纯度可能越高。这样会导致信息熵准则偏爱那些取值数目较多的属性。

信息增益率

为了解决信息增益原则的上述不足，给出信息增益率的定义：

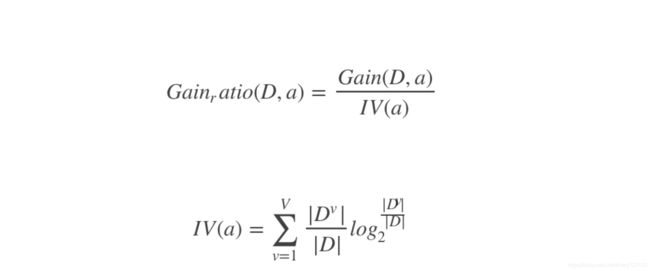
其中IV(a)，它是对于属性a的固有值，属性 a 的可能取值数目越大（即 V 越大）则IV(a) 的值通常会越大
例如IV(触感)=0.874 （V= 2），IV(色泽) = 1.58 （V = 3）,IV(编号)=4.088 （V= 17）

需要注意的是；信息增益率原则可能对取值数目较少的属性更加偏爱,为了解决这个问题，可以先找出信息增益在平均值以上的属性，在从中选择信息增益率最高的。

C4.5 算法

算法流程

C4.5算法过程跟ID3算法一样，只是选择特征的方法由信息增益改成信息增益比。

Python实现源码

def choose_best_feature_to_split(data_set):
    """
    按照最大信息增益比划分数据
    :param data_set: 样本数据，如： [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
    :return:
    """
    num_feature = len(data_set[0]) - 1 # 特征个数，如：不浮出水面是否可以生存  和是否有脚蹼
    base_entropy = calc_shannon_ent(data_set) # 经验熵H(D)
    best_info_gain_ratio = 0.0
    best_feature_idx = -1
    for feature_idx in range(num_feature):
        feature_val_list = [number[feature_idx] for number in data_set]  # 得到某个特征下所有值（某列）
        unique_feature_val_list = set(feature_val_list)  # 获取无重复的属性特征值
        new_entropy = 0
        split_info = 0.0
        for value in unique_feature_val_list:
            sub_data_set = split_data_set(data_set, feature_idx, value)
            prob = len(sub_data_set) / float(len(data_set))  # 即p(t)
            new_entropy += prob * calc_shannon_ent(sub_data_set)  # 对各子集香农熵求和
            split_info += -prob * log(prob, 2)
        info_gain = base_entropy - new_entropy  # 计算信息增益，g(D,A)=H(D)-H(D|A)
        if split_info == 0:  # fix the overflow bug
            continue
        info_gain_ratio = info_gain / split_info
        # 最大信息增益比
        if info_gain_ratio > best_info_gain_ratio:
            best_info_gain_ratio = info_gain_ratio
            best_feature_idx = feature_idx
    return best_feature_idx

基尼指数

基尼值

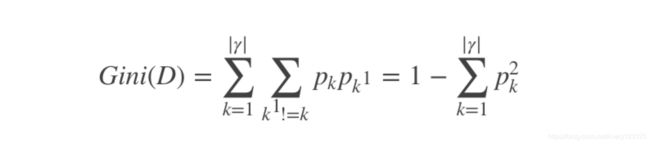形象的说，基尼值代表了从D中随机选择两个样本，其类别不一致的概率。

基尼指数

有了基尼值后，可以在此基础上定义基尼指数：

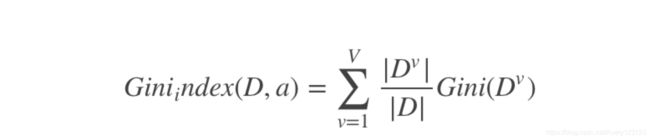
可以看出基尼指数越小，说明纯度越高，我们可以通过选择基尼指数小的属性来划分子节点。

CART 算法

算法流程

Python实现源码

# -*- coding: utf-8 -*-
import numpy as np
class Tree(object):
    def __init__(self, value=None, true_branch=None, false_branch=None, results=None, col=-1, summary=None, data=None):
        self.value = value
        self.true_branch = true_branch
        self.false_branch = false_branch
        self.results = results
        self.col = col
        self.summary = summary
        self.data = data
    def __str__(self):
        print(self.col, self.value)
        print(self.results)
        print(self.summary)
        return ""
def split_datas(rows, value, column):
    """
    根据条件分离数据集
    :param rows:
    :param value:
    :param column:
    :return:  (list1, list2)
    """
    list1 = []
    list2 = []
    if isinstance(value, int) or isinstance(value, float):
        for row in rows:
            if row[column] >= value:
                list1.append(row)
            else:
                list2.append(row)
    else:
        for row in rows:
            if row[column] == value:
                list1.append(row)
            else:
                list2.append(row)
    return list1, list2
def calculate_diff_count(data_set):
    """
    分类统计data_set中每个类别的数量
    :param datas:如：[[5.1, 3.5, 1.4, 0.2, 'setosa'], [4.9, 3, 1.4, 0.2, 'setosa'],....]
    :return: 如：{'setosa': 50, 'versicolor': 50, 'virginica': 50}
    """
    results = {}
    for data in data_set:
        # 数据的最后一列data[-1]是类别
        if data[-1] not in results:
            results.setdefault(data[-1], 1)
        else:
            results[data[-1]] += 1
    return results
def gini(data_set):
    """
    计算gini的值，即Gini(p)
    :param data_set: 如：[[5.1, 3.5, 1.4, 0.2, 'setosa'], [4.9, 3, 1.4, 0.2, 'setosa'],....]
    :return:
    """
    length = len(data_set)
    category_2_cnt = calculate_diff_count(data_set)
    sum = 0.0
    for category in category_2_cnt:
        sum += pow(float(category_2_cnt[category]) / length, 2)
    return 1 - sum
def build_decision_tree(data_set, evaluation_function=gini):
    """
    递归建立决策树，当gain=0时，停止回归
    :param data_set: 如：[[5.1, 3.5, 1.4, 0.2, 'setosa'], [4.9, 3, 1.4, 0.2, 'setosa'],....]
    :param evaluation_function:
    :return:
    """
    current_gain = evaluation_function(data_set)
    column_length = len(data_set[0])
    rows_length = len(data_set)
    best_gain = 0.0
    best_value = None
    best_set = None
    # choose the best gain
    for feature_idx in range(column_length - 1):
        feature_value_set = set(row[feature_idx] for row in data_set)
        for feature_value in feature_value_set:
            sub_data_set1, sub_data_set2 = split_datas(data_set, feature_value, feature_idx)
            p = float(len(sub_data_set1)) / rows_length
            # Gini(D,A)表示在特征A的条件下集合D的基尼指数，gini_d_a越小，样本集合不确定性越小
            # 我们的目的是找到另gini_d_a最小的特征，及gain最大的特征
            gini_d_a = p * evaluation_function(sub_data_set1) + (1 - p) * evaluation_function(sub_data_set2)
            gain = current_gain - gini_d_a
            if gain > best_gain:
                best_gain = gain
                best_value = (feature_idx, feature_value)
                best_set = (sub_data_set1, sub_data_set2)
    dc_y = {'impurity': '%.3f' % current_gain, 'sample': '%d' % rows_length}
    # stop or not stop
    if best_gain > 0:
        true_branch = build_decision_tree(best_set[0], evaluation_function)
        false_branch = build_decision_tree(best_set[1], evaluation_function)
        return Tree(col=best_value[0], value=best_value[1], true_branch=true_branch, false_branch=false_branch, summary=dc_y)
    else:
        return Tree(results=calculate_diff_count(data_set), summary=dc_y, data=data_set)
def prune(tree, mini_gain, evaluation_function=gini):
    """
    裁剪
    :param tree:
    :param mini_gain:
    :param evaluation_function:
    :return:
    """
    if tree.true_branch.results == None:
        prune(tree.true_branch, mini_gain, evaluation_function)
    if tree.false_branch.results == None:
        prune(tree.false_branch, mini_gain, evaluation_function)
    if tree.true_branch.results != None and tree.false_branch.results != None:
        len1 = len(tree.true_branch.data)
        len2 = len(tree.false_branch.data)
        len3 = len(tree.true_branch.data + tree.false_branch.data)
        p = float(len1) / (len1 + len2)
        gain = evaluation_function(tree.true_branch.data + tree.false_branch.data) \
               - p * evaluation_function(tree.true_branch.data)\
               - (1 - p) * evaluation_function(tree.false_branch.data)
        if gain < mini_gain:
            # 当节点的gain小于给定的 mini Gain时则合并这两个节点
            tree.data = tree.true_branch.data + tree.false_branch.data
            tree.results = calculate_diff_count(tree.data)
            tree.true_branch = None
            tree.false_branch = None
def classify(data, tree):
    """
    分类
    :param data:
    :param tree:
    :return:
    """
    if tree.results != None:
        return tree.results
    else:
        branch = None
        v = data[tree.col]
        if isinstance(v, int) or isinstance(v, float):
            if v >= tree.value:
                branch = tree.true_branch
            else:
                branch = tree.false_branch
        else:
            if v == tree.value:
                branch = tree.true_branch
            else:
                branch = tree.false_branch
        return classify(data, branch)
def load_csv():
    def convert_types(s):
        s = s.strip()
        try:
            return float(s) if '.' in s else int(s)
        except ValueError:
            return s
    data = np.loadtxt("datas.csv", dtype="str", delimiter=",")
    data = data[1:, :]
    data_set = ([[convert_types(item) for item in row] for row in data])
    return data_set
if __name__ == '__main__':
    data_set = load_csv()
    print data_set
    decistion_tree = build_decision_tree(data_set, evaluation_function=gini)
    print decistion_tree.results
    # prune(decistion_tree, 0.4)
    print classify([5.1,3.5,1.4,0.2], decistion_tree) # setosa
    print classify([6.8,2.8,4.8,1.4], decistion_tree) # versicolor
    print classify([6.8,3.2,5.9,2.3], decistion_tree) # virginica

输出结果：
{‘setosa’: 50}
{‘versicolor’: 47}
{‘virginica’: 43}

决策树的构造

决策树的构造是一个递归的过程，有三种情形会导致递归返回：

1、当前结点包含的样本全属于同一类别，这时直接将该节点标记为叶节点，并设为相应的类别；（最好的情形）

2、当前属性集为空，或是所有样本在所有属性上取值相同，无法划分，这时将该节点标记为叶节点，并将其类别设为该节点所含样本最多的类别；（属性用完）

3、当前结点包含的样本集合为空，不能划分，这时也将该节点标记为叶节点，并将其类别设为父节点中所含样本最多的类别。（数据用完）

基本流程

可以看出：决策树学习的关键在于如何选择划分属性，不同的划分属性得出不同的分支结构，从而影响整颗决策树的性能。属性划分的目标是让各个划分出来的子节点尽可能地“纯”，即属于同一类别。因此下面便是介绍量化纯度的具体方法，决策树最常用的算法有三种：ID3，C4.5和CART。

剪枝

剪枝是应对决策树过拟合的一种重要方法，主要分为以下两种：

预剪枝

预剪枝是自上而下的剪枝，指在决策树生成过程中，对每个结点进行事先估计，如果当前结点的划分不能带来决策树泛化性能的提升，则停止划分并将当前节点标记为叶结点。

留出法
留出法要求训练集和测试集的数据分布一致，类别比例相似，即采用分层采样。

预剪枝步骤：

第一步：将数据集按留出法要求划分为训练集和测试集

第二步：对训练集的所有样本基于某种指标（西瓜书的示例以信息增益为准则）选出最优划分属性，根据该结点划分前后的泛化性能差异判断该结点是否要根据该最优划分属性划分结点。

第三步：若划分了若干个结点，则继续对各个分支结点重复第二步的操作（第二步的“所有样本”转变成划分到该分支结点的样本子集，之后的计算都是基于对应的子集进行的），同时根据前面的三种情形做叶结点的判断，最终生成一棵决策树。

预剪枝流程：

假定有未剪枝的决策树如下：

通过测试集对结点进行的分类结果进行测试，根据其结果判断剪枝与否

预剪枝优缺点：

预剪枝决策树优点：
降低了过拟合的风险

显著减少了决策树的训练时间开销和测试时间开销

预剪枝决策树缺点：
需要注意的是，虽然有些分支的当前划分不能提升泛化性能，甚至可能导致泛化性能下降，但在其基础上进行的后续划分却有可能显著提升决策树的泛化性能！

预剪枝基于贪心的本质禁止这些分支展开，给预剪枝决策树带来了欠拟合的风险。

后剪枝

后剪枝是自下而上的剪枝，指对一棵已经生成的完整决策树自下而上地对非叶节点进行估计，如果将该结点对应的子树替换成叶结点能够带来决策树泛化性能的提升，则将该子树替换成叶结点。

后剪枝步骤：

第一步：将数据集按留出法要求划分为训练集和测试集

第二步：对训练集的所有样本基于某种指标（西瓜书的示例以信息增益为准则）选择最优划分属性，划分每一个可以划分的结点（先不比较泛化性能），生成一棵完整的未剪枝决策树（此时已经可以根据验证集得到该棵决策树的验证集精度）

第三步：从下而上对各个分支结点逐个进行如下操作：若该分支结点不展开，计算此时决策树的验证集精度，若验证集精度提高或不变，则剪枝不展开该结点。

后剪枝流程：

假定有未剪枝的决策树如下：
后剪枝在生成了完整的决策树后进行

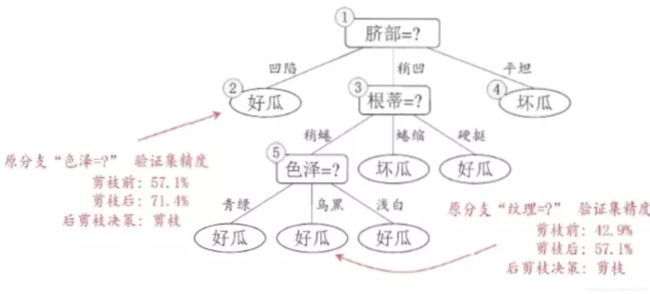
后剪枝优缺点：

后剪枝决策树优点：
保留更多分支，使得欠拟合风险很小

泛化性能往往优于预剪枝决策树

后剪枝决策树缺点：
后剪枝是在生成决策树后进行的，并且还要自底向上对书中每个非叶结点逐一考察，因此训练时间开销大

连续值与缺失值处理

连续值处理

由于连续值的取值数目不再有限，因此不可直接根据连续属性取值来对结点进行划分，需要使用连续值处理技术。最简单的就是C4.5中使用的二分法。

二分法

这就相当于该连续属性是每次都只有两个取值（小于等于 t 和大于 t）的离散属性，以此来划分样本。


如此一来连续值就可以生成如下的决策树：

缺失值处理

现实任务中常会遇到不完整样本，即样本的某些属性值缺失。
在此背景下，我们需要解决的两个问题：
1、如何在属性值缺失的情况下进行划分属性选择？

2、给定了划分属性，若样本在该属性上的值缺失，如何对样本进行划分？

如何在属性值缺失的情况下进行划分属性选择？

通过对每个样本x赋予权重，得到信息增益的推广式。

总体而言，就是在原始计算前添加了占比系数作为权重。

样本在划分属性上缺失值，如何对样本进行划分？

多变量决策树

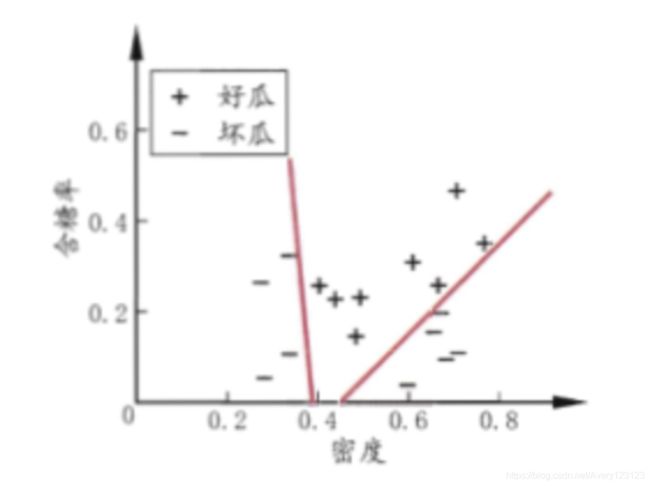
若将每个属性视为坐标空间中的一个坐标轴，则d个属性描述的样本就对应了d维空间中的一个数据点，对样本分类则意味着在这个坐标空间中寻找不同类样本的分类边界。

决策树形成的分类边界由若干个与坐标轴平行的分段组成，这些分类边界使得学习结果有较好的可解释性，因为每一段划分都对应了一个属性的取值的划分。


若能够使用斜的划分边界，就能够简化决策树模型。

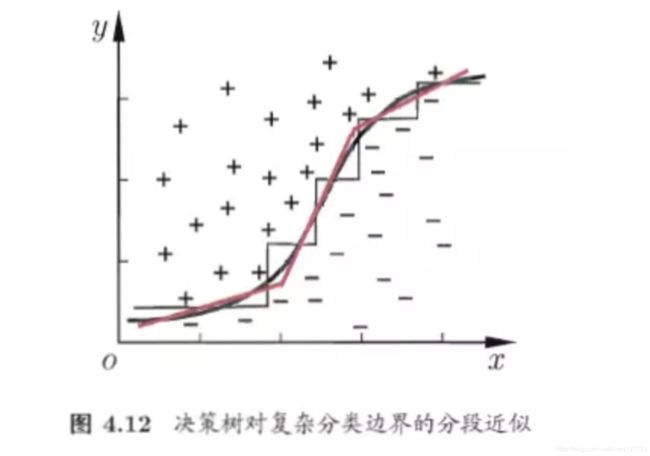
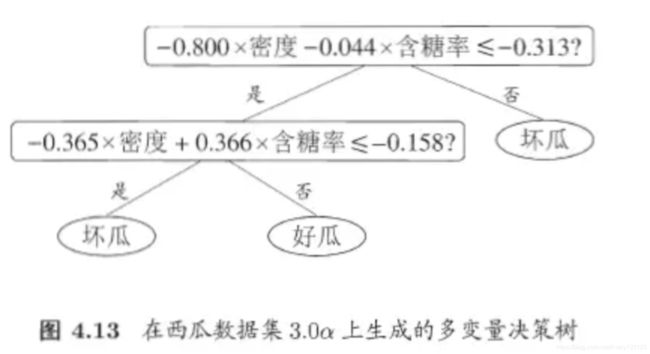
多变量决策树就是实现斜划分甚至更复杂划分的决策树。

与传统的单变量的决策树不同，多变量决策树的每个非叶子结点是对属性的线性组合进行测试，其每个非叶子结点是一个线性分类器，形如：

而多变量决策树在学习过程中是为每个非叶子结点建立合适的线性分类器。形如：

多变量决策树对应的分类边界：