《计算机视觉之三维重建》笔记5-双目视觉
北邮鲁鹏老师的课程《计算机视觉之三维重建(深入浅出sfm和SLAM核心算法)》 笔记
5,双目视觉
5.1,平行视图
引理1: [ a × ] B = B T [ ( B − 1 a ) × ] [a_\times]B=B^T[(B^{-1}a)_\times] [a×]B=BT[(B−1a)×]
引理2: e ′ = K ′ T e'=K'T e′=K′T
证明:
e ′ e' e′是 O 1 O_1 O1在相机 O 2 O_2 O2的像点
根据相机模型: e ′ = K ′ [ R , T ] [ 0 0 0 1 ] = K ′ T e'=K'[R,T]\left[ \begin{array}{c}0\\0 \\0 \\1 \end{array}\right]=K'T e′=K′[R,T]⎣⎢⎢⎡0001⎦⎥⎥⎤=K′T
定理:基础矩阵可写为: F = K ′ − T [ T × ] R K − 1 = [ e × ′ ] K ′ R K − 1 F=K'^{-T}[T_\times] RK^{-1}=[e'_\times]K'RK^{-1} F=K′−T[T×]RK−1=[e×′]K′RK−1
证明:
根据引理1,2, [ e × ′ ] K ′ = K ′ T [ ( K ′ − 1 e ′ ) × ] = K ′ T [ ( K ′ − 1 K ′ T ) × ] = K ′ T [ T × ] [e'_\times]K'=K'^T[(K'^{-1}e')_\times]=K'^T[(K'^{-1}K'T)_\times]=K'^T[T_\times] [e×′]K′=K′T[(K′−1e′)×]=K′T[(K′−1K′T)×]=K′T[T×]
∴ [ e × ′ ] K ′ R K − 1 = K ′ T [ T × ] R K − 1 = F \therefore [e'_\times]K'RK^{-1}=K'^T[T_\times]RK^{-1}=F ∴[e×′]K′RK−1=K′T[T×]RK−1=F
推论1:平行视图的基础矩阵: F = [ e × ′ ] = [ 0 0 0 0 0 − 1 0 1 0 ] F=[e'_\times]=\left[ \begin{array}{c} 0&0&0 \\ 0&0&-1 \\ 0&1&0 \end{array}\right] F=[e×′]=⎣⎡0000010−10⎦⎤
证明:
平行视图中: K = K ′ , R = I , T = ( T , 0 , 0 ) T K=K',R=I,T=(T,0,0)^T K=K′,R=I,T=(T,0,0)T
带入相机模型可得: e ′ = ( 1 , 0 , 0 ) T e'=(1,0,0)^T e′=(1,0,0)T,即极点在无穷远点且极线平行于X轴
带入定理可得: F = [ e × ′ ] K I K − 1 = [ e × ′ ] F=[e'_\times]KIK^{-1}=[e'_\times] F=[e×′]KIK−1=[e×′]
推论2:平行视图中像点 p = ( p u , p v , 1 ) T , p ′ = ( p u ′ , p v ′ , 1 ) T p=(p_u,p_v,1)^T,p'=(p'_u,p'_v,1)^T p=(pu,pv,1)T,p′=(pu′,pv′,1)T,则 p v = p v ′ p_v=p'_v pv=pv′
证明:
带入 p T F p ′ = 0 p^TFp'=0 pTFp′=0,可得 p v = p v ′ p_v=p'_v pv=pv′
三角测量问题:
已知 p , p ′ , K , K ′ , R , T p,p',K,K',R,T p,p′,K,K′,R,T,求 P P P的三维坐标。
平行视图的三角测量: p u − p u ′ = f B z p_u-p'_u=\frac{fB}{z} pu−pu′=zfB

可以得到深度图。应用:3D电影
问题:
- 如何保证平行视图
- 如何建立点对应
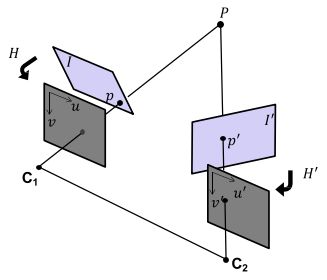
5.2,图像校正
对于问题1,可以通过图像校正,将两图像变换成平行视图
图像校正5步法:
- 匹配点对 p i ↔ p i ′ p_i\leftrightarrow p'_i pi↔pi′,大于8对
- 求基础矩阵 F F F,求极点 e i , e i ′ e_i,e'_i ei,ei′
通过8点法求得 F F F,得到极线 l i = F T p i ′ l_i=F^Tp'_i li=FTpi′,求解方程组{ l i T e = 0 l_i^Te=0 liTe=0}得到极点 e e e,同理可求得 e ′ e' e′
- 变换 H ′ = T − 1 G R T H'=T^{-1}GRT H′=T−1GRT,将 e ′ e' e′映射到无穷远 ( f , 0 , 0 ) (f,0,0) (f,0,0)
T = [ 1 0 − w i d t h / 2 0 1 − h e i g t h / 2 0 0 1 ] , w i d t h 、 h e i g h t T=\left[\begin{array}{c}1&0& -width/2\\ 0&1&-heigth/2\\ 0&0&1 \end{array}\right],width、height T=⎣⎡100010−width/2−heigth/21⎦⎤,width、height为图像的宽和高
经过 T T T变幻后的 e ′ e' e′坐标记为 ( e 1 ′ , e 2 ′ , 1 ) (e'_1,e'_2,1) (e1′,e2′,1)
R = [ α e 1 ′ e 1 ′ 2 + e 2 ′ 2 α e 2 ′ e 1 ′ 2 + e 2 ′ 2 0 − α e 2 ′ e 1 ′ 2 + e 2 ′ 2 α e 1 ′ e 1 ′ 2 + e 2 ′ 2 0 0 0 1 ] R=\left[\begin{array}{c} \alpha\frac{e'_1}{\sqrt{e_1'^2+e_2'^2}}& \alpha\frac{e'_2}{\sqrt{e_1'^2+e_2'^2}}& 0\\ -\alpha\frac{e'_2}{\sqrt{e_1'^2+e_2'^2}}& \alpha\frac{e'_1}{\sqrt{e_1'^2+e_2'^2}}& 0\\ 0&0&1 \end{array}\right] R=⎣⎢⎢⎡αe1′2+e2′2e1′−αe1′2+e2′2e2′0αe1′2+e2′2e2′αe1′2+e2′2e1′0001⎦⎥⎥⎤
其中 α = s i g n ( e 1 ′ ) \alpha=sign(e'_1) α=sign(e1′),经过 R R R变幻后 e ′ e' e′坐标为: ( f , 0 , 1 ) (f,0,1) (f,0,1)
G = [ 1 0 0 0 1 0 − 1 f 0 1 ] G=\left[\begin{array}{c} 1&0&0\\ 0&1&0\\ -\frac{1}{f}&0&1\\ \end{array}\right] G=⎣⎡10−f1010001⎦⎤
经过 G G G变幻后 e ′ e' e′坐标为: ( f , 0 , 0 ) (f,0,0) (f,0,0)
- 求解 H H H, min ∑ i d ( H p i , H ′ p i ′ ) \min\sum_{i}d(Hp_i,H'p'_i) min∑id(Hpi,H′pi′)
- 用 H , H ′ H,H' H,H′变换图像为平行视图
3,对应点搜索
图像矫正后,得到平行视图,在扫描线上寻找匹配点;
相关匹配/归一化相关匹配,效果一般,存在的问题:遮挡、透视缩短、基线选择、同质区域、重复模式
约束:
- 唯一性
- 单调性
- 平滑性
