KMeans算法------学习笔记

KMeans算法究竟是什么？

KMeans 算法接受输入量 k ；然后将n个数据对象划分为 k个聚类以便使得所获得的聚类满足：同一聚类中的对象相似度较高；而不同聚类中的对象相似度较小。聚类相似度是利用各聚类中对象的均值所获得一个“中心对象”（引力中心）来进行计算的
那么说通俗一点呢其实就是对一组数据进行分类，说的这里我们就要扩展一下了
KMeans和KNN这两种算法区别在哪呢？
其实很简单，KMeans算法虽然和KNN算法都用到了欧式距离的数学模型，但是KMeans算法是一种聚类算法，是一种非监督学习模型，这类模型是含有训练数据但是没有明确的分类标签，在我们拿到一组数据时想要对杂乱的数据进行聚类时使用的算法，而KNN算法呢是一种有监督的学习模型，它不仅有训练数据还有明确的分类标签

KMeans算法图解

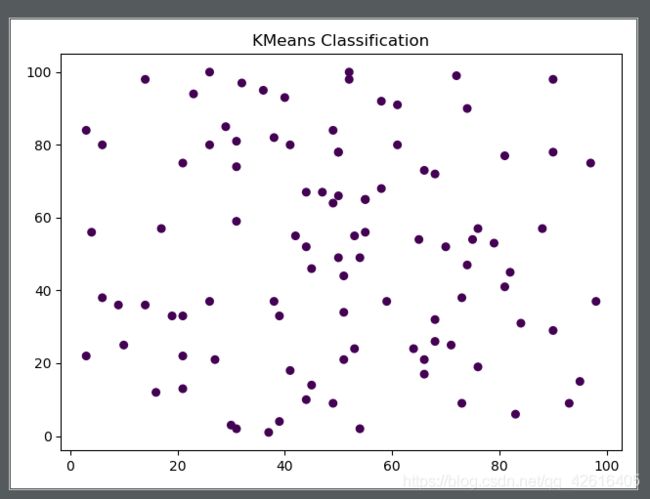
我们先在二维空间内随机生成100个无序的点，而我们要做的就是将这100个点分成K类，分成什么样子的K类呢，我们会在杂乱的点钟随机选择K个点作为中心点，通过计算每个点到中心点的距离找到100分别到哪个中心点是最近的那么我们就能大概划分出K个区域在不同区域内的点到他们中心点距离最小，然后我们知道这个中心点是随机选出的我们无法去控制，但是我们还要尽量约束每个点让他们的类分的更加细腻，所以我们将去计算每个区域内的点的坐标，通过计算平均坐标选取最优的中心点从而划分出最优的区域，通过中心点不断地偏移一次次迭代，我们将会划分出最合理的区域当然这个区域与我们最开始选择的中心点是有一定关系

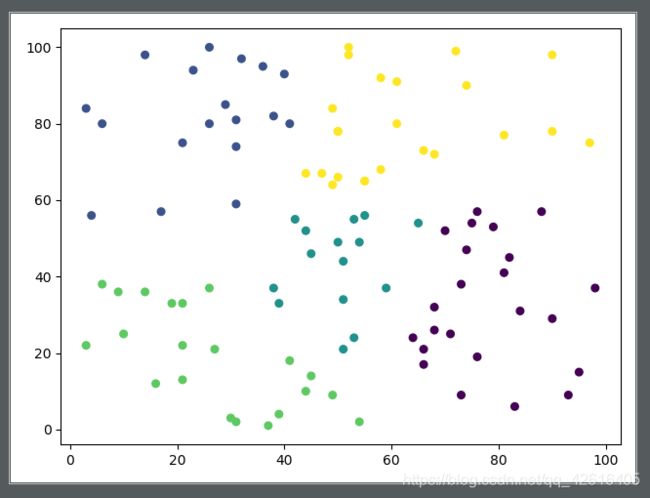
这就是我们划分后的结果这里我们是在二维空间内进行划分K的值是5所以我们分成5类，当然空间越小，点越密集我们划分出来的类就越规则
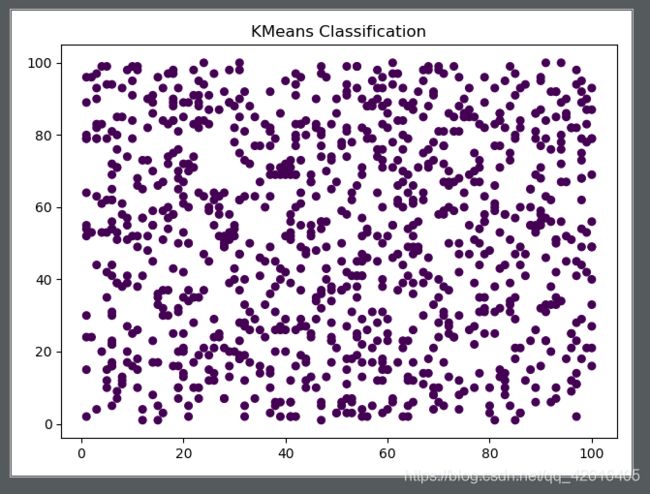
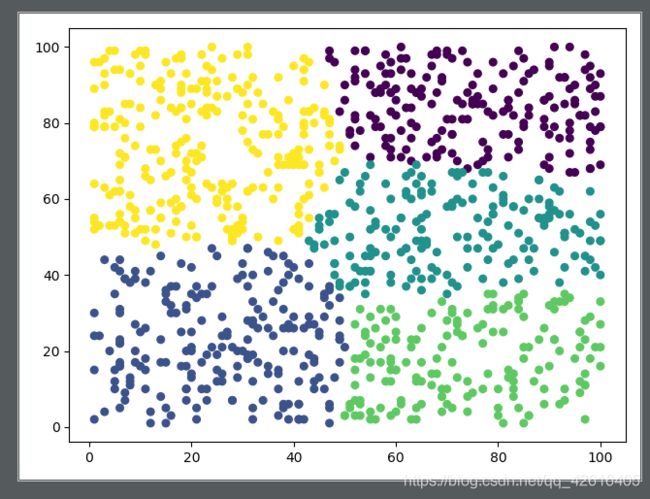
下面我们输出一下平面下1000个无序点分成5类

算法进阶------应用

说了那么多我们的算法除了计算出乱七八糟的点似乎没有派上什么用场？
这其实是我在第一次尝试写这个算法时最想去问的？怎么应用于实际，算法其实是一种工具，而Kmeans算法就是我们数据挖掘时最好的工具，我们数据采集到一大批的杂乱数据，而我们就可以以数据中的属性为维度对杂乱的进行分类从而找到其最优的推论，当机器去分析杂乱的数据样本后当我们再去给他数据的时候他就可以直接对数据进行归纳
比如一个人身高，体重，年龄我们需要通过这些属性去分析它的患病风险，这样就可以建立三维的空间用三种属性作为空间内的坐标，找到点与点之间的联系从而建立集群，这在医学，电商等等的领域里都有了实际的应用，所以我说，算法是一种可以应用的艺术品，我们在不断提高看得见摸得着的工具时，算法这种足以改变世界的工具也在不断地自我优化着，

第一次实现KMeans算法

（第一次实现性能和功能性都是ok的但是还没有按照人工智能算法模式在走，摸着石头过河版）

import random
class Point:
    '''
    设置一个点将点封装成对象，这样做的好处在于后面我们需要将一些繁琐的数据产生关联，封装成对象可以直接建立联系
    方便理解
    缺点需要循环遍历多次浪费时间，无法实现多维空间的转换，下一篇博客将对其进行改进
    '''
    def  __init__(self):
        self.__x = None#对象的属性坐标
        self.__y = None#对象的属性坐标
        self.__Data = None#用来储存其他数据建立点与点之间的联系
    def __str__(self):
        x=str(self.x)
        y=str(self.y)
        return "("+x+","+y+")"
    @property
    def x(self):
        return self.__x
    @x.setter
    def x(self,x):
        self.__x=x
    @property
    def y(self):
        return self.__y
    @y.setter
    def y(self,y):
        self.__y=y
    @property
    def Data(self):
        return self.__Data
    @Data.setter
    def Data(self,Data):
        self.__Data=Data
class SportTools:
    def MakePoint(self):
        '''
        随机生成2维空间内的点
        :return: 1个随机点
        '''
        point = Point()
        point.x = random.randint(-200, 200)
        point.y = random.randint(-200, 200)
        return point
    def MakePoints(self,num):
        '''
        随机生成num个二维空间内的点
        :param num: 多少个点
        :return: 点对象的列表
        '''
        pointlist=[]
        for n in range(num):
            point=self.MakePoint()
            pointlist.append(point)
        return pointlist
    def MakePointK(self,pointlist,N=5):
        '''
        选取Kmeans算法的第一次的随机点，也就是对这类数据进行分几类处理
        :param pointlist: 需要分类的数据
        :param N: 分几类
        :return: 返回选取的随机点列表
        '''
        return random.sample(pointlist,N)
    def TwoPointDistence(self,PointK,point):
        '''
        利用欧式公式计算两点之间距离
        欧式公式是一种已知两点坐标求两点距离的公式
        :param PointK: A点
        :param point: B点
        :return: A.B两点之间距离
        '''
        return ((PointK.x-point.x)**2+(PointK.y-point.y)**2)**0.5
    def Kmeans(self,pointlist,K):
        '''
        我在这里对我的Kmeans算法进行了方法封装
        :param pointlist:要进行分类的点的列表
        :param K:中心点的列表
        :return:返回我们最后找到的中心点也就是最后划分完的类，因为我是用类进行封装的点，
                这样我就可以通过Data属性对他们的类别进行储存从而找出所有的点的类别
        '''
        N=[]#定义一个空的列表N用来储存我们最后的返回结果
        for point in pointlist:
            distance = []#定义一个距离列表这里不仅定义了它也在每次循环中将列表重置
            for PointK in K:#这里循环K我们就可以得到每一次中心点到其他100个点的距离
                dis=self.TwoPointDistence(PointK,point)#算出中心点到随机点的距离
                PointK.Data=dis#这里我们暂时用Data来存储一个距离
                distance.append(PointK.Data)#将第一次算出来的5个距离封装进列表
            for PointK in K:#选出最小的距离进行归类处理
                if PointK.Data==min(distance):
                    point.Data=PointK#这里我们将他的类别存放到Data属性中这样我们只需要遍历Data就知道他们的类别了
        for PointK in K:
            arg = []#分类处理，将一类放到一个元组
            for point in pointlist:
                if point.Data==PointK:
                    arg.append(point)
            countx = 0#这是两个坐标计数器为了找到新的中心值
            county = 0
            # print(arg)
            for i in arg:
                countx=i.x+countx
                county=i.y+county
            # print(arg)
            x,y=countx/len(arg),county/len(arg)#计算出新中心点的坐标
            spK=Point()#建立新中心点
            spK.x=x
            spK.y=y
            N.append(spK)#将新中心点放到开始建立的N列表中
        count=0#建立中心点坐标差值求和的计数器
        for i in range(len(N)):
            count=self.TwoPointDistence(K[i],N[i])+count
        if count/len(N)<=0.000000000001:#判断界限确定中心点是否是最优中心点
            print(count/len(N))
            #这里以上我们就已经完成了第一次寻找中心点的工作我们用判断条件去限制它为了让他不断自我约束是最终得到的中心点不再偏移
            return N,pointlist
        else:
            print(count/len(N))
            #递归调用上面的函数不断寻找最优的中心点
            return self.Kmeans(pointlist,N)
tool = SportTools()
list1=tool.MakePoints(100)
K=tool.MakePointK(list1)
p,spolist=tool.Kmeans(list1,K)
for i in p:
    print(i)

如果你有认真看完上面的代码（你是个勇士）
这里是改进版

import random
import matplotlib.pyplot as plt
class KMeans():
```python

    
    def __init__(self, k=1):
        '''
        :param k: k代表分类数
        '''
        self.__k = k
        self.__data = []       # 存放原始数据
        self.__pointCenter = []  # 存放中心点，第一次获得的中心点通过随机方式在__data里随机出来
        self.__result = []
        for i in range(k):
            self.__result.append([])  # [[],[],[],[],[]]
            pass
        pass

    def fit(self, data, threshold, times=50000):
        '''
        进行模型训练
        :param data: 训练数据
        :param threshold: 阈值，退出条件
        :return:
        '''
        self.__data = data
        self.randomCenter()
        print(self.__pointCenter)
        centerDistance = self.calPointCenterDistance(self.__pointCenter, self.__data)

        # 对原始数据进行分类，将每个点分到离它最近的中心点
        i = 0
        for temp in centerDistance:
            index = temp.index(min(temp))
            self.__result[index].append(self.__data[i])
            i += 1
            pass
        # 打印分类结果
        # print(self.__result)
        oldCenterPoint = self.__pointCenter
        newCenterPoint = self.calNewPointCenter(self.__result)

        while self.calCenterToCenterDistance(oldCenterPoint, newCenterPoint) > threshold:
            times -= 1
            result = []
            for i in range(self.__k):
                result.append([])
                pass
            # 保存上次的中心点
            oldCenterPoint = newCenterPoint
            centerDistance = self.calPointCenterDistance(newCenterPoint, self.__data)

            # 对原始数据进行分类，将每个点分到离它最近的中心点
            i = 0
            for temp in centerDistance:
                index = temp.index(min(temp))
                result[index].append(self.__data[i]) # result = [[[10,20]]]
                i += 1
                pass

            newCenterPoint = self.calNewPointCenter(result)
            print(self.calCenterToCenterDistance(oldCenterPoint, newCenterPoint))
            self.__result = result
            pass
        self.__pointCenter = newCenterPoint
        return newCenterPoint, self.__result
        pass

    def calCenterToCenterDistance(self, old, new):
        '''
        计算两次中心点之间的距离，求和求均值
        :param old: 上次的中心点
        :param new: 新计算的中心点
        :return:
        '''
        total = 0
        for point1, point2 in zip (old, new):
            total += self.distance(point1, point2)
            pass
        return total / len(old)
        pass

    def calPointCenterDistance(self, center, data):
        '''
        计算每个点和每个中心点之间的距离
        :return:
        '''
        centerDistance = []
        for temp in data:
            centerDistance.append([self.distance(temp, point) for point in center])
            pass
        print(centerDistance)
        return centerDistance
        pass

    def calNewPointCenter(self, result):
        '''
        计算新的中心点
        :param result:
        :return:
        '''
        newCenterPoint = []
        for temp in result:
            # 转置
            temps = [[temp[x][i] for x in range(len(temp)) ] for i in range(len(temp[0]))]
            point = []
            for t in temps:
                # 对每个维度求和，去平均
                point.append(sum(t)/len(t)) # mean
                pass
            newCenterPoint.append(point)
            pass
        print(newCenterPoint)
        return newCenterPoint
        pass
    def distance(self, pointer1, pointer2):
        '''
        计算两个点之间的距离，支持任意维度，欧式距离
        :param pointer1:
        :param pointer2:
        :return:
        '''
        distance = (sum([(x1 - x2)**2 for x1, x2 in zip(pointer1, pointer2)]))**0.5
        return distance
        pass

    def randomCenter(self):
        '''
        从原始的__data里随机出最开始进行计算的k个中心点
        :return:
        '''
        while len(self.__pointCenter) < self.__k:
            # 随机一个索引
            index = random.randint(0, len(self.__data) - 1)
            # 判断中心点是否重复，如果不重复，加入中心点列表
            if self.__data[index] not in self.__pointCenter:
                self.__pointCenter.append(self.__data[index])
                pass
            pass
        pass
    pass
    `if __name__ == "__main__":
    data = [[random.randint(1, 100), random.randint(1, 100)] for i in range(1000)]
    for i in range(1):
        kmeans = KMeans(k=5)
        centerPoint, result = kmeans.fit(data, 0.0001)
        print(centerPoint)
        plt.plot()
        plt.title("KMeans Classification")
        i = 0
        tempx = []
        tempy = []
        color = []
        for temp in result:
            temps = [[temp[x][i] for x in range(len(temp))] for i in range(len(temp[0]))]
            color += [i] * len(temps[0])
            tempx += temps[0]
            tempy += temps[1]

            i += 2
            pass
         #这里是负责打点的看不懂可以略过color也是
        plt.scatter(tempx, tempy, c=[1]*1000, s=30)
        plt.show()
        plt.scatter(tempx, tempy, c=color, s=30)
        plt.show()
        pass
    pass`