【论文阅读】PGCL:Prototypical Graph Contrastive Learning
目录
- 摘要
- 1 引言
- 2 相关工作
- 3 准备工作
-
- 3.1 问题定义
- 3.2 GNN
- 3.3 图对比学习
- 4 PGCL
-
- 4.1 相关视图的聚类一致性
- 4.2 重加权对比目标
- 5 实验
摘要
之前的对比方法存在一个抽样偏差问题,即负样本很可能与正样本具有相同的语义结构,从而导致性能下降。为了减轻该抽样偏差,本文提出了一种原型图对比学习(PGCL)方法。
具体来说,PGCL通过将语义相似的图聚类到同一组中来对图数据的底层语义结构进行建模,同时鼓励同一图的不同增强的聚类一致性。然后,给定一个正样本,通过从那些与正样本集群不同的集群中提取图来执行负采样,这确保了正样本和负样本之间的语义差异。此外,对于一个正样本,PGCL基于其负样本的原型(聚类中心)与正样本原型之间的距离对它的负样本重新赋予权重,使得那些具有中等原型距离的负样本获得相对较大的权重,以保证正样本与负样本之间的语义差异。这种重新赋予权重策略被证明比均匀抽样更有效。
1 引言
现有的自监督图对比学习方法具有以下局限性:
- 现有的方法主要关注于实例级结构相似性的建模,只保留实例周围的局部相似性,但未能发现整个数据分布中的底层全局结构。但在实践中,大多数情况下,图数据中都存在潜在的全局结构。
- 如图所示1,从整个数据分布中均匀采样负样本可能会导致负样本在语义上与正样本相似。

整个数据集的全局语义结构由PGCL在原型向量(即可训练的聚类中心)中描述。
2 相关工作
基于聚类的对比学习: GraphLoG应用K-means聚类来捕获图的语义结构,但使用K-means可能会导致原型的分配不平衡。与GraphLoG相比,PGCL增加了原型分配必须划分为相同大小的子集的约束条件,并将其表述为最优传输问题。此外,PGCL的目标是通过从与正样本集群不同的集群中采样负样本,并根据其原型距离重新赋权负样本,来解决抽样偏差。
3 准备工作
3.1 问题定义
局部实例结构。 我们将不同图例之间的局部成对相似性称为局部实例结构。在对比学习的范式中,相似的图对的嵌入预计在潜在空间中很接近,而不同的图对应该映射得很远。
仅对局部实例结构进行建模通常不足以发现整个数据集底层的全局语义。我们非常希望捕获数据的全局语义结构,其定义如下:
全局语义结构。 来自现实世界的图结构数据通常可以被组织为各种语义集群。潜在空间中邻近图的嵌入应该体现全局结构,从而反映原始数据的语义模式。
问题设置。 给定一组未标记图 G = { G i } i = 1 N \mathcal{G}=\{G_i\}^N_{i=1} G={Gi}i=1N,无监督图表示学习的目的是学习每个图 G i ∈ G G_i∈\mathcal{G} Gi∈G的低维向量 z i ∈ R D z_i∈\mathbb{R}^D zi∈RD,这有利于图分类等下游任务。
3.2 GNN
我们将一个图实例表示为 G = ( V , E ) G=(\mathcal{V},\mathcal{E}) G=(V,E),节点集为 V \mathcal{V} V,边集为 E \mathcal{E} E。在第 k k k次迭代时,节点 v v v在第 k k k层的嵌入为:
![]()
然后,可以通过使用读出函数聚合所有节点表示来获得图级表示,即:
![]()
READOUT表示平均或更复杂的图级池化函数。
3.3 图对比学习
4 PGCL
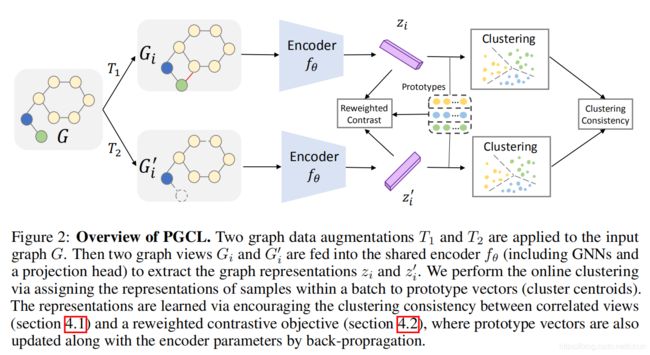
如图2所示,鼓励对增强视图的表示进行聚类,以具有相同的原型(聚类中心)。
4.1 相关视图的聚类一致性
形式上,考虑一个将图例 G i G_i Gi映射到表示向量 z i ∈ R D z_i∈\mathbb{R}^D zi∈RD的图神经网络 z i = f θ ( G i ) z_i=f_θ(G_i) zi=fθ(Gi)。我们可以将所有表示 z i z_i zi聚类成 K K K个簇,其中心由一组可训练原型向量 { c 1 , … , c K } \{c_1,…,c_K\} {c1,…,cK}表示。为了简洁起见,我们用 C ∈ R K × D C∈\mathbb{R}^{K×D} C∈RK×D表示。在实践中, C C C可以通过单个线性层来实现。这样,给定一个 G i G_i Gi图,我们可以通过计算表示 z i = f θ ( G i ) z_i=f_θ(G_i) zi=fθ(Gi)和 K K K原型之间的相似性来执行聚类,如下:
![]()
同样地,将 G i ′ G_i' Gi′分配给原型的预测 p ( y ∣ z i ′ ) p(y|z_i') p(y∣zi′)也可以通过 z i ′ z_i' zi′来计算。为了鼓励两个相关视图 G i G_i Gi和 G i ′ G_i' Gi′之间的聚类一致性,我们用 z i z_i zi(而不是 z i ′ z_i' zi′)来预测 G i ′ G_i' Gi′的聚类分配,反之亦然。形式上,我们通过最小化平均交叉熵损失来定义聚类一致性目标:

其中, q ( y ∣ z i ′ ) q(y|z_i') q(y∣zi′)是视图 G i ′ G_i' Gi′的原型分配,可以作为 z i z_i zi的预测 p ( y ∣ z i ) p(y|z_i) p(y∣zi)的目标。一致性目标作为一个正则化器,鼓励来自同一图的视图的相似性。如果我们交换方程(5)中 z i z_i zi和 z i ′ z_i' zi′的位置,我们可以得到另一个类似的目标。最终的一致性正则化器可以通过两个目标的和导出:
![]()
一致性正则化器可以解释为通过比较集群分配而不是表示来比较多个图的视图。在实际应用中,分布 q q q的优化面临着存在的简并性问题,因为通过将所有数据点分配给一个(任意的)原型,就可以简单地最小化(5)。为了避免这种情况,我们添加了原型分配必须被平均分区的约束。我们以小批量的方式计算目标,以实现有效的优化:

方程(7)中的目标在 q q q中是组合的,因此可能很难优化。然而,这是最优传输问题的一个实例,可以相对有效地解决。为了更清楚地看到它,我们将两个联合概率的 K × N K×N K×N矩阵表示为:
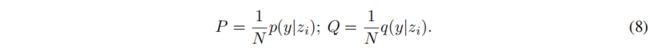
然后,我们可以通过以小批量方式将矩阵 Q Q Q约束为传输多面体来实现相等的分割:
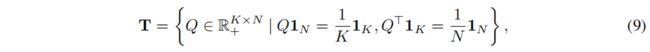
其中, 1 K 1_K 1K表示维度为 K K K的全是1的向量。这些约束要求每个原型在批处理中平均选择至少 N K \frac{N}{K} KN次。然后,方程(7)中的目标函数可以重新写为:
![]()
其中, ⟨ ⋅ ⟩ \langle·\rangle ⟨⋅⟩是两个矩阵之间的Frobenius点积, l o g log log是用于元素级的。优化方程(10)总是导致一个整数解,尽管将 Q Q Q放宽到连续多面体 T T T而不是离散多面体。我们通过采用Sinkhorn-Knopp算法的快速版本来解决传输问题,并且方程(10)的解采用规范化矩阵的形式,如下所示:
![]()
其中, α α α和 β β β是两个重正化向量,指数化是元素级的。选择 η η η是为了权衡收敛速度与原始传输问题的接近程度,在我们的例子下,它是一个固定的值。重正化向量可以使用迭代的Sinkhorn-Knopp算法,使用少量的矩阵乘法来计算。
4.2 重加权对比目标
在本节中,我们将介绍如何通过从不同的集群采样图,并对负样本进行重新加权来减轻抽样偏差问题。给定一个正样本及其集群,我们可以简单地通过从不同的集群中提取“正确的”负样本来实现这一点。方程(3)可以扩展为:
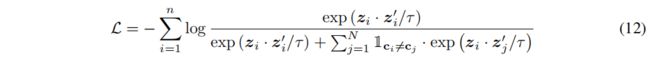
其中, c i c_i ci和 c j c_j cj分别为图 G i G_i Gi和 G j G_j Gj的原型向量, 1 c i ≠ c j \mathbb{1}_{c_i≠c_j} 1ci=cj是表示两个样本是否来自不同簇的指标。

除了根据其集群的区别来选择负样本外,我们还希望避免在潜在空间中选择远离正样本的太简单的样本。直观地说,理想的负样本应该与正样本有适度的距离。为了实现这一需求,我们求助于控制它们的原型距离,而不是它们的直接距离。如图3所示,一方面,如果负样本的原型太接近query的原型,负样本仍然可以与query共享类似的语义结构(例如,附近的青色集群)。另一方面,如果负样本的原型(如紫色簇)离query的原型很远,这意味着负样本和query彼此相距很远,可以很好地区分,这实际上对表示学习没有帮助。
为此,我们进一步重新计算方程(12)中负样本项的权重,并将重新加权的目标定义为:

其中, w i j w_{ij} wij为负对 ( G i , G j ) (G_i,G_j) (Gi,Gj)的权重, M i = N ∑ j = 1 N w i j M_i=\frac{N}{\sum_{j=1}^Nw_{ij}} Mi=∑j=1NwijN是归一化因子。我们利用余弦距离来测量两个原型之间的距离,如: D ( c i , c j ) = 1 − c i ⋅ c j ∣ ∣ c i ∣ ∣ 2 ∣ ∣ c j ∣ ∣ 2 \mathcal{D}(c_i,c_j)=1-\frac{c_i·c_j}{||c_i||_2||c_j||_2} D(ci,cj)=1−∣∣ci∣∣2∣∣cj∣∣2ci⋅cj。然后根据上述原型距离,将 w i j w_{ij} wij定义高斯函数的形式:
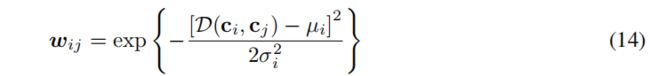
其中, μ i \mu_i μi和 σ i \sigma_i σi分别为 D ( c i , c j ) \mathcal{D}(c_i,c_j) D(ci,cj)的平均值和标准差。
最终的训练目标为:
![]()
最小化该损失函数来优化原型 C C C和图编码器的参数 θ θ θ。