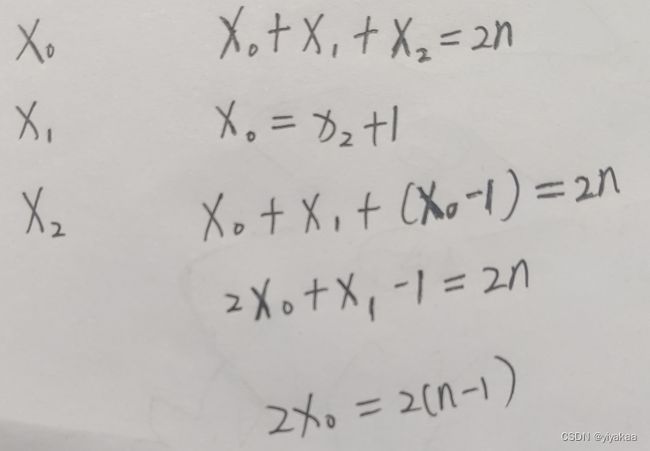数据结构与算法6：树与二叉树(叶子节点个数、节点个数、前序遍历、后序遍历、中序遍历、二叉树遍历、平衡树)

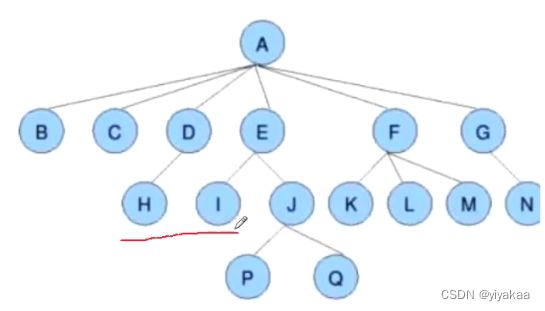
节点的度：一个节点含有的子树个数称为该节点的度：如下：A的为6
叶节点或终端节点：度为0的节点称为叶节点：如图：B、C、H、I…等节点为叶节点
非终端节点或分支节点：度不为0的节点；如图：D、E、F、G…等节点为分支节点
双亲结点或父节点：若一个结点含有子节点，则这个结点称为其子节点的父节点；如图：A是B的双亲
孩子结点或子节点：一个节点含有的子树的根节点称为该节点的子节点；B是A的孩子节点
兄弟节点：具有相同父节点的节点互称为兄弟节点（亲兄弟）；B、C是兄弟节点
树的度：一棵树中，最大的节点的度称为树的度；下图中树的度为6
节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，依次类推
树的高度或深度：树中节点的最大层次；如图树的高度为4
节点的祖先：从根到该节点所经分支上的所有节点；如图，A是所有节点的祖先
子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如图所有节点都是A的子孙
森林：由m（m>0）棵互不相交的多棵树的集合称为森林

定义二叉树并进行前序遍历

#define _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
#include 
typedef int BTDataType;
typedef struct BinaryTreeNode {
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;

void PrevOrder(BTNode* root) {
	if (root == NULL) {
		return;
	}
	printf("%c-> ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
	
}

int main() {
	BTNode* A = (BTNode*)malloc(sizeof(BTNode));
	A->data = 'A';
	A->left = NULL;
	A->right = NULL;

	BTNode* B = (BTNode*)malloc(sizeof(BTNode));
	B->data = 'B';
	B->left = NULL;
	B->right = NULL;

	BTNode* C = (BTNode*)malloc(sizeof(BTNode));
	C->data = 'C';
	C->left = NULL;
	C->right = NULL;

	BTNode* D = (BTNode*)malloc(sizeof(BTNode));
	D->data = 'D';
	D->left = NULL;
	D->right = NULL;

	BTNode* E = (BTNode*)malloc(sizeof(BTNode));
	E->data = 'E';
	E->left = NULL;
	E->right = NULL;

	A->left = B;
	A->right = C;
	B->left = D;
	B->right = E;

	PrevOrder(A);
	printf("NULL\n");

	return 0;
}

特殊的二叉树：

1. 满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树，，也就是说，如果一个二叉树的层数为K，且结点总数为(2^k)-1，则它就是满二叉树。
2. 完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为k的，有n个结点的二叉树，当且仅当每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。要注意满二叉树时一种特殊的完全二叉树。

二叉树的性质：

1. 若规定根节点的层数为1，则一棵非空二叉树的第i层最多有2^(i-1)个结点
2. 若规定根结点的层数为1，则深度为h的二叉树的最大结点数是2^h-1
3. 对任何一颗二叉树，如果度为0其叶节点个数为n0，度为2的分支结点个数为n2，则有n0 = n2 + 1
4. 若规定根结点的层数为1，具有n个结点的满二叉树的深度，h = LogN+1

练习题：

1. 某二叉树共有399个结点，其中有199个度为2的结点，则该二叉树中的叶子结点数为200

2. 在具有2n个结点的完全二叉树中，叶子结点个数为n

3. 一颗完全二叉树得节点数位为531个，那么这棵树得高度为

示例：计算二叉树的叶子节点个数、节点个数、前序遍历、后序遍历、中序遍历

#define _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
#include 
typedef int BTDataType;
typedef struct BinaryTreeNode {
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;
//前序遍历
void PrevOrder(BTNode* root) {
	if (root == NULL) {
		return;
	}
	printf("%c->", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);	
}

//中序遍历
void ZOrder(BTNode* root) {
	if (root == NULL) {
		return;
	}
	ZOrder(root->left);
	printf("%c->", root->data);
	ZOrder(root->right);
}

//后序遍历
void HOrder(BTNode* root) {
	if (root == NULL) {
		return;
	}
	HOrder(root->left);
	HOrder(root->right);
	printf("%c->", root->data);
}

//结点个数
int TreeSize(BTNode* root) {
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

//叶子节点个数
int TreeLeafSize(BTNode* root) {
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL) 
		return 1;
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}


int main() {
	BTNode* A = (BTNode*)malloc(sizeof(BTNode));
	A->data = 'A';  
	A->left = NULL;
	A->right = NULL;

	BTNode* B = (BTNode*)malloc(sizeof(BTNode));
	B->data = 'B';
	B->left = NULL;
	B->right = NULL;

	BTNode* C = (BTNode*)malloc(sizeof(BTNode));
	C->data = 'C';
	C->left = NULL;
	C->right = NULL;

	BTNode* D = (BTNode*)malloc(sizeof(BTNode));
	D->data = 'D';
	D->left = NULL;
	D->right = NULL;

	BTNode* E = (BTNode*)malloc(sizeof(BTNode));
	E->data = 'E';
	E->left = NULL;
	E->right = NULL;

	A->left = B;
	A->right = C;
	B->left = D;
	B->right = E;
	//先序
	PrevOrder(A);
	printf("NULL\n");

	//中序
	ZOrder(A);
	printf("NULL\n");
	//后序
	HOrder(A);
	printf("NULL\n");

	int i = TreeSize(A);
	printf("%d\n", i);
	int j = TreeLeafSize(A);
	printf("%d\n", j);
	return 0;
}

算法1：给定一个二叉树，找出其最大深度。

示例：

给定二叉树 [3,9,20,null,null,15,7]，返回它的最大深度 3 。

思路：二叉树为空时高度为0；非空时，分解子问题，先求左右子树的深度，我的深度等于左右子树深度大的+1。

int maxDepth(struct TreeNode* root){
    if(root == NULL)
        return 0;
    int leftDepth = maxDepth(root->left);
    int rightDepth = maxDepth(root->right);

    return leftDepth>rightDepth ? leftDepth+1:rightDepth+1;
}

算法2：给定一个二叉树，判断它是否是高度平衡的二叉树。

高度平衡二叉树定义为一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例1：

输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

输入：root = [1,2,2,3,3,null,null,4,4]
输出：false
示例 3：

输入：root = []
输出：true

 int maxDepth(struct TreeNode* root){
    if(root == NULL)
        return 0;
    int leftDepth = maxDepth(root->left);
    int rightDepth = maxDepth(root->right);

    return leftDepth>rightDepth ? leftDepth+1:rightDepth+1;
}

bool isBalanced(struct TreeNode* root){
    if(root == NULL)
        return true;
    int leftDepth = maxDepth(root->left);
    int rightDepth = maxDepth(root->right);

    return abs(leftDepth-rightDepth) < 2 && isBalanced(root->left) && isBalanced(root->right);
}

算法3：二叉树的前序遍历

带调试1代码OJ：

#include 
typedef int BTDataType;
typedef struct TreeNode {
     BTDataType val;
     struct TreeNode *left;
     struct TreeNode *right;
 }TreeNode;

int TreeSize(TreeNode* root) {
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

void _prevOrder(TreeNode* root, int* a, int* pi) {
    if (root == NULL) {
        return;
    }
    a[*pi] = root->val;
    (*pi)++;
    _prevOrder(root->left, a, pi);
    _prevOrder(root->right, a, pi);
}
//如果想返回两个值时候，第一种方法是返回结构体，第二种方法是这里的这种，*returnSize = size
int* preorderTraversal(TreeNode* root, int* returnSize) {
    int size = TreeSize(root);
    int* a = (int*)malloc(size * sizeof(int));
    int i = 0;
    _prevOrder(root, a, &i);
    *returnSize = size;
    return a;
}

int main() {
    TreeNode* A = (TreeNode*)malloc(sizeof(TreeNode));
    A->val = 1;
    A->left = NULL;
    A->right = NULL;

    TreeNode* B = (TreeNode*)malloc(sizeof(TreeNode));
    B->val = 2;
    B->left = NULL;
    B->right = NULL;

    TreeNode* C = (TreeNode*)malloc(sizeof(TreeNode));
    C->val = 3;
    C->left = NULL;
    C->right = NULL;

    A->left = B;
    B->left = NULL;
    B->right = NULL;
    A->right = C;
    C->left = NULL;
    C->right = NULL;

    int size = 0;
    int* a = preorderTraversal(A,&size);
    return 0;
}

带调试2代码OJ：

#include 
#include 
#include 



struct TreeNode {
     int val;
     struct TreeNode *left;
     struct TreeNode *right;
 };


int TreeSize(struct TreeNode* root) {
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}


void _prevOrder(struct TreeNode* root, int* a, int* pi) {
    if (root == NULL) {
        return;
    }
    a[*pi] = root->val;
    (*pi)++;
    _prevOrder(root->left, a, pi);
    _prevOrder(root->right, a, pi);
}
//如果想返回两个值时候，第一种方法是返回结构体，第二种方法是这里的这种，*returnSize = size
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    int size = TreeSize(root);
    int* a = (int*)malloc(size * sizeof(int));
    int i = 0;
    _prevOrder(root, a, &i);
    *returnSize = size;

    return a;
}

int main() {

    struct TreeNode node1;
    struct TreeNode node2;
    struct TreeNode node3;
    node1.val = 1;
    node1.left = &node2;
    node1.right = &node3;

    node2.val = 2;
    node2.left = NULL;
    node2.right = NULL;

    node3.val = 3;
    node3.left = NULL;
    node3.right = NULL;

    int size = 0;
    int* a = preorderTraversal(&node1,&size);

    return 0;
}

二叉树遍历

编写一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。例如如下的先序遍历字符串：ABC##DE#G##F### 其中” # “ 表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。

示例：

输入：ABC##DE#G##F###
输出：C B E G D F A

#define _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
#include 

typedef char BTDataType;

typedef struct TreeNode {
    BTDataType val;
    struct TreeNode* left;
    struct TreeNode* right;
}TNode;

TNode* CreateTree(char* a, int* pi) {
    if (a[*pi] == '#') {
        (*pi)++;
        return NULL;
    }
    TNode* root = (TNode * )malloc(sizeof(TNode));
    if (root == NULL) {
        printf("malloc fail\n");
        exit(-1);
    }
    root->val = a[*pi];
    (*pi)++;
    root->left = CreateTree(a, pi);
    root->right = CreateTree(a, pi);
    return root;
}

void InOrder(TNode* root) {
    if (root == NULL) {
        return;
    }
    InOrder(root->left);
    printf("%c ",root->val);
    InOrder(root->right);
}

int main() {
    char str[100];
    scanf("%s", str);

    int i = 0;
    TNode* root = CreateTree(str, &i);

    InOrder(root);

    return 0;
}