常见聚类算法及使用--Affinity Propagation（AP）

前言

对于聚类算法，大家应该都已经略知一二，比如说它是无监督，不需要标签来监督它的学习，我们需要的是在特定场景下将这些未被标注的数据进行自然分组。
那么看完这片文章，你将收获如下几个方面的点：

• 聚类是在输入数据的特征空间中查找自然组的无监督问题；
• 对于所有数据集，有许多不同的聚类算法和单一的最佳方法；
• 在 scikit-learn 机器学习库的 Python 中如何实现、适配和使用顶级聚类算法。

一些准备

一些聚类算法要求您指定或猜测数据中要发现的群集的数量，而另一些算法要求指定观测之间的最小距离，其中示例可以被视为“关闭”或“连接”。因此，聚类分析是一个迭代过程，在该过程中，对所识别的群集的主观评估被反馈回算法配置的改变中，直到达到期望的或适当的结果。scikit-learn 库提供了一套不同的聚类算法供选择。下面会为大家解读一些比较流行的聚类算法。
每个算法都提供了一种不同的方法来应对数据中发现自然组的挑战。没有最好的聚类算法，也没有简单的方法来找到最好的算法为您的数据没有使用控制实验。

• 依赖库安装（前提是你已安装了Python解释器）：

  pip install scikit-learn==0.22.1
  

• 创建数据集：

  # 综合分类数据集
  from numpy import where
  from sklearn.datasets import make_blobs
  from matplotlib import pyplot as plt
  
  # 创建数据集
  # X为样本特征，Y为样本簇类别， 共1000个样本，每个样本2个特征，共4个簇，
  # 簇中心在[-1,-1], [0,0],[1,1], [2,2]， 簇方差分别为[0.4, 0.2, 0.2, 0.2]
  X, y = make_blobs(n_samples=1000, n_features=2, 
                  centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
                  cluster_std=[0.4, 0.3, 0.2, 0.1],
                  random_state=9)
  # 数据可视化
  plt.scatter(X[:, 0], X[:, 1], marker='o')
  plt.show()
  

  代码大家可以在 IDE 或者 jupyter notebook 中运行，得到比较有区分度的两个类群样本点如下：
  
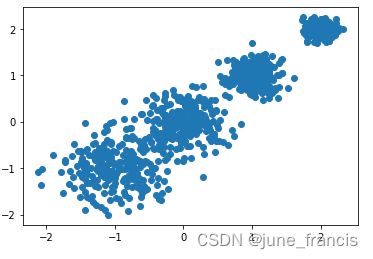
  下面我会应用创建的数据集于不同的聚类算法。

亲和力传播（Affinity Propagation）

此算法的基本思想是将全部数据点都当作潜在的聚类中心(称之为 exemplar )，然后数据点两两之间连线构成一个网络( 相似度矩阵 )，再通过网络中各条边的消息( responsibility 和 availability )传递计算出各样本的聚类中心。
大致的收敛迭代过程如下：

先介绍算法中的一些特殊名词：

• Exemplar：指的是聚类中心，也就是 K-Means 中的质心。
• Similarity（相似度）：点 j 作为点 i 的聚类中心的能力，记为 S(i,j) 。一般使用负的欧式距离，所以 S(i,j) 越大，表示两个点距离越近，相似度也就越高。使用负的欧式距离，相似度是对称的，如果采用其他算法，相似度可能就不是对称的。
• Preference：指点 i 作为聚类中心的参考度(不能为0)，取值为 S相似度 对角线的值(下图1中红色标注部分)，此值越大，则为聚类中心的可能性就越大。如果没有被设置，则一般设置为 S相似度 值的中值。
• Responsibility（吸引度）：指点 k 适合作为数据点 i 的聚类中心的程度，记为 r(i,k) 。如下图2中红色箭头所示，表示点 i 给点 k 发送信息，是一个点 i 选择点 k 作为聚类中心的评估过程。
• Availability (归属度)：指点 i 选择点 k 作为其聚类中心的适合程度，记为 a(i,k) 。如下图3中红色箭头所示，表示点 k 给点 i 发送信息，是一个点 k 选点 i 作为聚类中心的评估过程。
• Damping factor (阻尼系数)：主要是起收敛作用的。

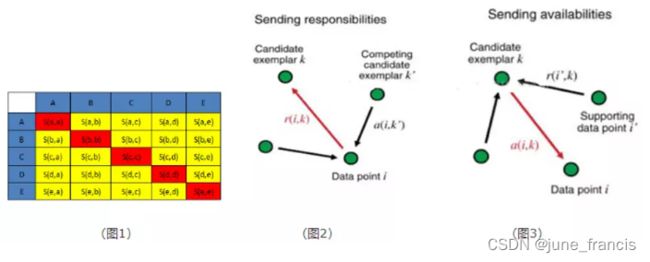
在实际计算应用中，最重要的两个参数（也是需要手动指定）是 Preference 和 Damping factor 。前者约束了聚类数量的多少，值越大聚类数量越多；后者控制算法收敛效果。

关于此算法的详细聚类过程，我们则以以下数据进行演示：
假设我们现在有如下样本，共5个维度：
$$Table1：PreferencesofFiveParticipants$$

Participant	Tax Rate	Fee	Interest Rate	Quantity Limit	Price Limit
Alice	3	4	3	2	1
Bob	4	3	5	1	1
Cary	3	5	3	3	3
Doug	2	1	3	3	2
Edna	1	1	3	2	3

相似度矩阵（Similarity Matrix）

相似度矩阵中每个单元是用两个样本对应值的差的平方和取负值得到的，对角线上的除外。
例如这里我们来计算一下 Alice 和 Bob 的相似度：
$$(3-4{)}^2+(4-3{)}^2+(3-5{)}^2+(2-1{)}^2+(1-1{)}^2=7$$
如上所述，他们之间的相似度是 -7 。
最后，我们得到如下结果：

Participant	Alice	Bob	Cary	Doug	Edna
Alice	0	-7	-6	-12	-17
Bob	-7	0	-17	-17	-22
Cary	-6	-17	0	-18	-21
Doug	-12	-17	-18	0	-3
Edna	-17	-22	-21	-3	0

当聚类中心为对角线上的单元格选择了比较小的值，那么AP算法会快速收敛并得到少量的聚类中心，反之亦然。因此。我们使用表格中最小的值 -22 去填充相似度矩阵中的 0 对角线单元格。
$$Table2：SimilarityMatrix$$

Participant	Alice	Bob	Cary	Doug	Edna
Alice	-22	-7	-6	-12	-17
Bob	-7	-22	-17	-17	-22
Cary	-6	-17	-22	-18	-21
Doug	-12	-17	-18	-22	-3
Edna	-17	-22	-21	-3	-22

吸引度矩阵（Responsibility Matrix）

一开始我们构造一个全为 0 的矩阵作为初始 归属度矩阵（Availability Matrix），接下来使用如下公式计算每一个 吸引度矩阵（Responsibility Matrix） 中的单元格的值：
$$r(i,k)\leftarrow s(i,k)-\underset{k^{{}^{\prime }}\ne k}{\max }\{a(i,k^{{}^{\prime }})+s(i,k^{{}^{\prime }})\}\text{\hspace{1em}(1)}$$
其中： i 和 k 分别表示对应矩阵中的行、列索引。

举个栗子：现在我们来计算 Bob(column) 对 Alice(row) 的 吸引度（Responsibility），这里套用上面的公式即为：用 Bob(column) 对 Alice(row) 的 相似度（Similarity） 为 -7 减去 Alice 这一行除了 Bob 对其它人相似度的最大值 -6，结果为 -1 。
那么我们很快便可得到如下吸引度矩阵：
$$Table3：ResponsibilityMatrix$$

Participant	Alice	Bob	Cary	Doug	Edna
Alice	-16	-1	1	-6	-11
Bob	10	-15	-10	-10	-15
Cary	11	-11	-16	-12	-15
Doug	-9	-14	-15	-19	9
Edna	-14	-19	-18	14	-19

归属度矩阵（Availability Matrix）

接下来我们使用一个独立的式子去更新 归属度矩阵 中的 对角线 上的单元格而不是直接删除：
$$a(k,k)\leftarrow \sum \underset{i^{{}^{\prime }}\ne k}{\max }\{0,r(i^{{}^{\prime }},k)\}\text{\hspace{1em}(2)}$$
其中： i 和 k 分别指矩阵中的行、列索引。
实际上这个公式计算的是除了指定行以外对应列所有单元格值大于 0 的总和。比如现在我们要得到 Alice 的自我归属度，只需要将除了 Alice 那行的 自我吸引度值除外的当列所有值加和即可：
$$10+11+0+0=21$$
接下来的式子用于计算 非对角线 单元格的归属度：
$$a(i,k)\leftarrow \min \{0,r(k,k)+\sum \underset{i^{{}^{\prime }}\notin \{i,k\}}{\max }\{0,r(i^{{}^{\prime }},k)\}\}\text{\hspace{1em}(3)}$$
在这里同样的我们来举个例子：求 $a(Cary,Edna)$ ，$r(Edna,Edna)=-19$ ，求和项 $\max (0,r(Alice,Edna))+\max (0,r(Bob,Edna))+\max (0,r(Doug,Edna))=0+0+9=9$ ，$a(Cary,Edna)=\min (0,-19+9)=-10$ 。
同理， $a(Doug,Bob)=\min (0,-15+0+0+0)=-15$ 。
我们可以得到如下归属度矩阵：
$$Table4：AvailabilityMatrix$$

Participant	Alice	Bob	Cary	Doug	Edna
Alice	21	-15	-16	-5	-10
Bob	-5	0	-15	-5	-10
Cary	-6	-15	1	-5	-10
Doug	0	-15	-15	14	-19
Edna	0	-15	-15	-19	9

评估矩阵（Criterion Matrix）

评估矩阵中的单元格值是由对应位置的归属度值和吸引度值相加而得：
$$c(i,k)\leftarrow r(i,k)+a(i,k)\text{\hspace{1em}(4)}$$
例如： $c(Bob(column),Alice(row))=-1+-15=-16$ 。
那么我们可以得到如下评估矩阵：
$$Table5：CriterionMatrix$$

Participant	Alice	Bob	Cary	Doug	Edna
Alice	5	-16	-15	-11	-21
Bob	5	-15	-25	-15	-25
Cary	5	-26	-15	-17	-25
Doug	-9	-29	-30	-5	-10
Edna	-14	-34	-33	-5	-10

我们一般将评估矩阵中取得最大值的一些点作为聚类中心（这些点可能又多个行组成），比如在我们这个例子中， Alice，Bob 和 Cary 共同组成一个聚类簇，而 Doug 和 Edna 则组成了第二个聚类簇。
在实践中，我们一般会在训练模型前将不同量纲的特征进行归一化（因为归根结底当前算法比较依赖样本之间的距离）。

代码演示

sklearn.cluster.AffinityPropagation 参数设置介绍：

• damping : 衰减系数，默认为 0.5；
• convergence_iter : 迭代 convergence_iter 次后聚类中心如果没有变化，则算法结束，默认为15；
• max_iter : 最大迭代次数，默认为200；
• copy : 是否在元数据上进行计算，默认True，在复制后的数据上进行计算；
• preference : S矩阵的对角线上的值，默认为输入的S矩阵值的中位数；
• affinity :S矩阵（相似度），默认为 euclidean（欧氏距离） 矩阵（使用负的欧式距离的平方作为计算结果），即对传入的X计算距离矩阵，也可以设置为 precomputed，那么X就作为相似度矩阵。

训练完AP聚类之后可以获得的结果有：

• cluster_centers_indices_ : 聚类中心的位置
• cluster_centers_ : 聚类中心
• labels_ : 类标签
• affinity_matrix_ : 最后输出的A矩阵
• n_iter_ ：迭代次数

接下来我们利用文章开头构建的样本使用AP算法来完成一次聚类：

# 亲和力传播聚类
import numpy as np
from sklearn.cluster import AffinityPropagation

# 定义模型
model = AffinityPropagation(preference=-50, damping=0.9)
# 匹配模型
model.fit(X)
# 为每个示例分配一个集群
y_hat = model.predict(X)
# 检索唯一类簇
clusters = np.unique(y_hat)
# 为每个类簇的样本创建散点图
for cluster in clusters:
  # 获取此类簇样本的行索引
  row_ix = np.where(y_hat == cluster)
  # 创建这些样本的散点图
  plt.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
plt.show()

运行上述代码，得到如下样本分布散点图：

模型评估：

from sklearn import metrics

# 聚类效果评估
print("Homogeneity: %0.3f" % metrics.homogeneity_score(y, y_hat))
print("Completeness: %0.3f" % metrics.completeness_score(y, y_hat))
print("V-measure: %0.3f" % metrics.v_measure_score(y, y_hat))
print("Adjusted Rand Index: %0.3f"
      % metrics.adjusted_rand_score(y, y_hat))
print("Adjusted Mutual Information: %0.3f"
      % metrics.adjusted_mutual_info_score(y, y_hat))
print("Silhouette Coefficient: %0.3f"
      % metrics.silhouette_score(X, y_hat, metric='sqeuclidean'))

输出结果为：

Homogeneity: 0.934
Completeness: 0.935
V-measure: 0.935
Adjusted Rand Index: 0.941
Adjusted Mutual Information: 0.935
Silhouette Coefficient: 0.827

根据散点图及各个聚类指标即可看出，当前参数下的AP算法对当前样本的聚类效果是非常不错的。

总结

AP聚类算法 与经典的 K-Means 聚类算法相比，具有很多独特之处：

1. 无需指定聚类“数量”参数。AP聚类不需要指定K（经典的K-Means）或者是其他描述聚类个数（SOM中的网络结构和规模）的参数，这使得先验经验成为应用的非必需条件，适用的场景更多。

2. 明确的质心（聚类中心点）。样本中的所有数据点都可能成为AP算法中的质心，叫做Examplar，而不是由多个数据点求平均而得到的聚类中心（如 K-Means）。

3. 对距离矩阵的对称性没要求。AP通过输入相似度矩阵来启动算法，因此允许数据呈非对称，数据适用范围非常大。

4. 初始值不敏感。多次执行AP聚类算法，得到的结果是完全一样的，即不需要进行随机选取初值步骤（对比K-Means的随机初始值）。

5. 算法复杂度较高，为 O(N*N*logN)，而 K-Means 只是 O(N*K) 的复杂度。因此当 N 比较大时( N>3000 )，AP聚类算法往往需要消耗更多的时间。

6. 若以 误差平方和 来衡量算法间的优劣，AP聚类比其他方法的误差平方和都要低。（无论k-center clustering重复多少次，都达不到AP那么低的误差平方和）

7. AP算法相对K-Means鲁棒性强且准确度较高，但没有任何一个算法是完美的，AP聚类算法的主要缺点：

   • AP聚类应用中需要手动指定 Preference 和 Damping factor，这其实是原有的聚类“数量”控制的变体。
   • 算法较慢。由于AP算法复杂度较高，运行时间相对K-Means长，这会使得尤其在海量数据下运行时耗费的时间很多。

关于AP算法与K-means算法的运行时间对比：

import time
from sklearn.cluster import KMeans

# 生成测试数据
np.random.seed(0)
centers = [[1, 1], [-1, -1], [1, -1]]
kmeans_time = []
ap_time = []
for n in [100, 500, 1000]:
    X, labels_true = make_blobs(n_samples=n, centers=centers, cluster_std=0.7)
 
    # 计算K-Means算法时间
    k_means = KMeans(init='k-means++', n_clusters=3, n_init=10)
    t0 = time.time()
    k_means.fit(X)
    kmeans_time.append([n, (time.time() - t0)])
 
    # 计算AP算法时间
    ap = AffinityPropagation()
    t0 = time.time()
    ap.fit(X)
    ap_time.append([n, (time.time() - t0)])
 
print('K-Means time', kmeans_time[:10])
print('AP time', ap_time[:10])
 
# 图形展示
km_mat = np.array(kmeans_time)
ap_mat = np.array(ap_time)
plt.figure()
plt.bar(np.arange(3), km_mat[:, 1], width=0.3, color='b', label='K-Means', log='True')
plt.bar(np.arange(3) + 0.3, ap_mat[:, 1], width=0.3, color='g', label='AffinityPropagation', log='True')
plt.xlabel('Sample Number')
plt.ylabel('Computing time')
plt.title('K-Means and AffinityPropagation computing time ')
plt.legend(loc='upper center')
plt.show()

得到如下结果：

K-Means time [[100, 0.0870048999786377], [500, 0.05600333213806152], [1000, 0.3390192985534668]]
AP time [[100, 0.024001598358154297], [500, 1.4930853843688965], [1000, 18.196040868759155]]

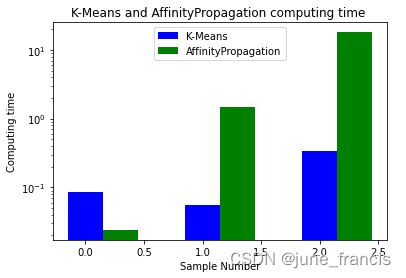
图中为了更好的展示数据对比，已经对时间进行 log 处理，但可以从输出结果直接读取真实数据运算时间。由结果可以看到：当样本量为 100 时，AP的速度要大于K_Means；当数据增加到 500 甚至 1000 时，AP算法的运算时间要大大超过K-Means算法。

参考文献

1. https://scikit-learn.org/stable/modules/generated/sklearn.cluster.AffinityPropagation.html?highlight=sklearn+cluster+affinity
2. https://towardsdatascience.com/unsupervised-machine-learning-affinity-propagation-algorithm-explained-d1fef85f22c8
3. https://flashgene.com/archives/93104.html