常见聚类算法及使用--均衡的迭代并减少聚类中心的层次聚类（BIRCH）

前言

前面文章给大家介绍了 关于层次聚类算法的实现，那么本文给大家继续介绍层次聚类的优化算法 BIRCH 。

大家都知道像 K-means 这样的聚类算法比较有局限性，而且在大数据场景下很难处理，特别是在有限的内存和较慢的CPU硬件条件下。我相信这样的情况常规的聚类算法都没有办法确保随着数据量的不断增加而保证很好的聚类的质量和高效的运行时间。于是 BIRCH 应运而生： Balanced Iterative Reducing and Clustering using Hierarchies (BIRCH) 是一种应用层次聚类方法将大数据场景下的样本首先生成较小而且紧凑的类簇，并且这写类簇能够保留更可能多的信息。通过生成这样的一些关键的聚类信息，因此 BIRCH 也常被用作其它聚类算法的启蒙。
然而它也有一个主要的缺陷–它只能处理数值型数据。

算法实现

BIRCH的核心

BIRCH 算法有两个核心概念需要先了解一下：

Clustering Feature (CF)

BIRCH 会将大数据集初始化成多个小型的数据簇，这些构成密集区域的数据叫做 簇特征条目（Clustering Feature entries），每一条簇特征是有一个三元组数据构成：$(N,LS,SS)$ 。$N$ 表示当前簇中样本点的数量， $LS$ 表示簇中样本点的线性加和，例如：${\sum }_{i=1}^N{X}_i$ ，$SS$ 表示当前簇中样本点的平方和，例如：${\sum }_{i=1}^N{X}_i^2$ 。
同时，每一个簇特征条目很有可能是其它簇特征条目的组成部分，这个说法在论文里面是有被提到，叫做 CF Aditivity Theorem (CF 可加定理) ，这个定理被证明：两个相近的簇，它们的 CF 分别用 $CF1=(N_1,L{S}_1,S{S}_1)$ 和 $C{F}_2=(N_2,L{S}_2,S{S}_2)$ 表示，那么由这两个相近的簇组成的新簇的 CF 可表示为： $CF=(N_1+N_2,L{S}_1+L{S}_2,S{S}_1+S{S}_2)$ 。

Clustering Feature Tree (CF Tree)

CF Tree 实际上就是 CF 的一种紧凑的表示方式，它是一种叶子结点包含一个子簇的树状结构。
CF Tree 中的每一个 CF entry 都包含一个指向子节点的指针，每个节点的 CF entry 由它指向的子节点所包含的所有子簇的 CF entry 的加和组成。
当然了，每个叶子节点中包含的 CF entry 的数目是有限制的，每个非叶子节点最多包含的 CF entry 同样也是有约束的，在后面的 API 参数中会介绍到。
在论文中，对于 CF Tree 是这样描述的：

A CF tree is a height-balanced tree with two parameters: branching factor B and threshold T.

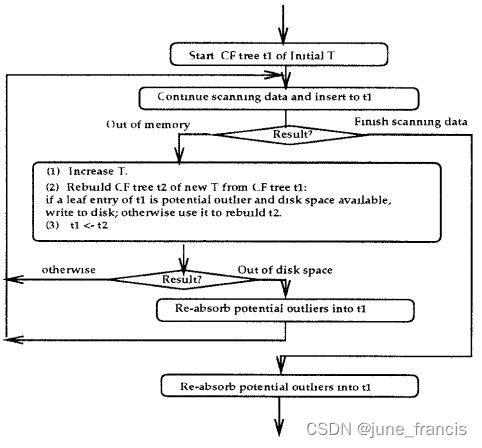
BIRCH 构建 CF tree 的过程如下：

关于 CF tree 如何利用有限的 memory 完成对大数据集的聚类，以及如何有效的区分异常值，大致过程如下，详细的过程说明大家可以根据文末的链接阅读相关论文：

API及其参数

本文以 scikit-learn 中 BIRCH 的 API 实现为例：

class sklearn.cluster.Birch(*, threshold=0.5, branching_factor=50, n_clusters=3, compute_labels=True, copy=True)

• threshold：通过合并新样本得到的子簇的半径和距离最近的子簇的半径必须小于这个值，否则会新建一个子簇。如果这个值设的非常小，那么会促进叶子节点继续分裂，反之亦然。默认值为 0.5。
• branching_factor：每个子节点所包含的最大 CF 子簇的个数。如果超过了这个值，则节点会分裂（包含的子簇重新分配）成两部分。默认值为 50。
• n_clusters：最终聚类得到的类簇个数。默认值为 3。如果设为 None，聚类的最后一步不会执行，会返回聚类的中间结果。

案例实现

构造样本

  # 综合分类数据集
  import numpy as np
  from sklearn.datasets import make_blobs
  from matplotlib import pyplot as plt

  # 创建数据集
  # X为样本特征，Y为样本簇类别， 共1000个样本，每个样本2个特征，共4个簇，
  # 簇中心在[-1,-1], [0,0],[1,1], [2,2]， 簇方差分别为[0.4, 0.2, 0.2, 0.2]
  X, y = make_blobs(n_samples=1000, n_features=2, 
                  centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
                  cluster_std=[0.4, 0.3, 0.2, 0.1],
                  random_state=9)
  # 数据可视化
  plt.scatter(X[:, 0], X[:, 1], marker='o')
  plt.show()

展示结果如下：

实例化API完成对样本的聚类：

from sklearn.cluster import Birch

# Creating the BIRCH clustering model
model = Birch(branching_factor = 50, n_clusters = 4, threshold = 0.8)
 
# Fit the data (Training)
model.fit(X)
 
# Predict the same data
pred = model.predict(X)
 
# Creating a scatter plot
plt.scatter(X[:, 0], X[:, 1], c = pred, cmap = 'rainbow', alpha = 0.7, edgecolors = 'b')
plt.show()

展示效果如下：

这个参数是我调整过的，大家可以继续在这个基础上进行微调，以达到更好的聚类效果。
最后，BIRCH 聚类后的结果可以当做其它聚类算法的输入，比如 AgglomerativeClustering ，大家可以根据需要自行尝试。

参考文献

1. https://www.cs.sfu.ca/CourseCentral/459/han/papers/zhang96.pdf
2. https://scikit-learn.org/stable/modules/generated/sklearn.cluster.Birch.html
3. https://www.geeksforgeeks.org/ml-birch-clustering/