使用极限学习机进行股市预测（Matlab代码实现）

    目录

1 概述

2 运行结果

3 参考文献

‍4 Matlab代码

---

1 概述

极限学习机（Extreme Learning Machine,ELM）作为前馈神经网络学习中一种全新的训练框架,在行为识别、情感识别和故障诊断等方面被广泛应用,引起了各个领域的高度关注和深入研究.ELM最初是针对单隐层前馈神经网络的学习速度而提出的,之后又被众多学者扩展到多隐层前馈神经网络中.该算法的核心思想是随机选取网络的输入权值和隐层偏置,在训练过程中保持不变,仅需要优化隐层神经元个数.网络的输出权值则是通过最小化平方损失函数,来求解Moore-Penrose广义逆运算得到最小范数最小二乘解.相比于其它传统的基于梯度的前馈神经网络学习算法,ELM具有实现简单,学习速度极快和人为干预较少等显著优势,已成为当前人工智能领域最热门的研究方向之一.ELM的学习理论表明,当隐层神经元的学习参数独立于训练样本随机生成,只要前馈神经网络的激活函数是非线性分段连续的,就可以逼近任意连续目标函数或分类任务中的任何复杂决策边界.近年来,随机神经元也逐步在越来越多的深度学习中使用,而ELM可以为其提供使用的理论基础.

运行脚本的说明：

1. 打开 ELM_run.m 脚本并更改脚本参数的值。
2. 运行脚本

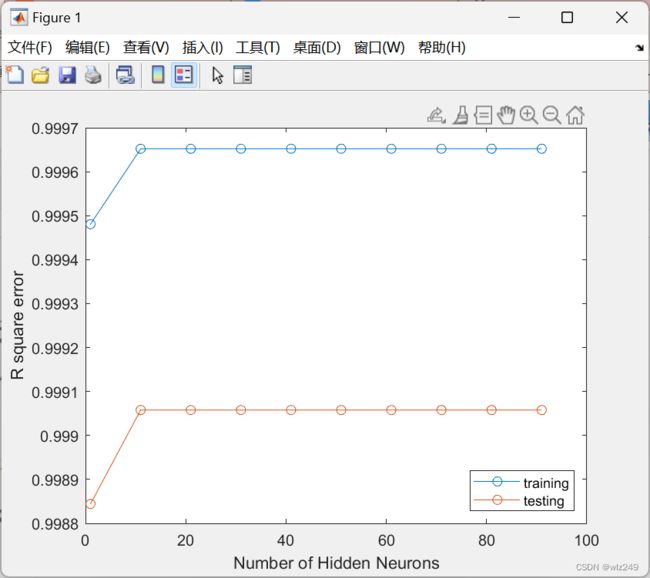
2 运行结果

3 参考文献

[1]徐睿,梁循,齐金山,李志宇,张树森.极限学习机前沿进展与趋势[J].计算机学报,2019,42(07):1640-1670.

‍4 Matlab代码

主函数部分代码：

%%Introduction to the ELM run script
%Please the change the arguments according to your needs

%% important arguments for the script
activationFunction = 'linear';
dataFile = 'newstocks.txt';
rowsToSkip = 1;
columnsToSkipFromLeft = 1; 
columnsToSkipFromRight = 1;
hiddenLayerSize = 10;
trainingPercentage = 50;
daysToPredict = 5;

%% data loading and preprocessing
% load data
pureData = csvread(dataFile,rowsToSkip,columnsToSkipFromLeft);

% acquire X
X = pureData(daysToPredict:end,1:end - columnsToSkipFromRight);

% get number of entries and features
[nEntries, nFeatures] = size(X);

% acquire Y 
Y = pureData(1:nEntries,1:nFeatures);

% finding split points in data
percTraining = trainingPercentage/100; 
endTraining  = ceil(percTraining * nEntries);

% dividing X and Y
% training data 
trainX = X(1:endTraining,:); 
trainY = Y(1:endTraining,:);

% testing data
testX = X(endTraining+1:end,:);
testY = Y(endTraining+1:end,:);

%% creation and training of ELM model

% create ELM
ELM = ELM_MatlabClass(nFeatures,hiddenLayerSize,activationFunction);

% train ELM on the training dataset
ELM = train(ELM,trainX,trainY);

%% validation of ELM model
predictionTest = predict(ELM,testX);
disp('Statistics when predicting on testing data');
fprintf('Testing Rsquare(close to 1 means nice prediction) = %3.3f\n',computeR2(testX,predictionTest));
fprintf('Testing Root mean square error of open price = %3.3f\n',computeRMSE(testX(:,1),predictionTest(:,1)));
fprintf('Testing Root mean square error of high price = %3.3f\n',computeRMSE(testX(:,2),predictionTest(:,2)));
fprintf('Testing Root mean square error of low price = %3.3f\n',computeRMSE(testX(:,3),predictionTest(:,3)));
fprintf('Testing Root mean square error of close price = %3.3f\n',computeRMSE(testX(:,4),predictionTest(:,4)));

% compute and report accuracy on training dataset
predictionTrain = predict(ELM,trainX);
disp('Statistics when predicting on training data');
fprintf('Training Rsquare(close to 1 means nice prediction) = %3.3f\n',computeR2(trainX,predictionTrain));
fprintf('Training Root mean square error of open price = %3.3f\n',computeRMSE(trainX(:,1),predictionTrain(:,1)));
fprintf('Training Root mean square error of high price = %3.3f\n',computeRMSE(trainX(:,2),predictionTrain(:,2)));
fprintf('Training Root mean square error of low price = %3.3f\n',computeRMSE(trainX(:,3),predictionTrain(:,3)));
fprintf('Training Root mean square error of close price = %3.3f\n',computeRMSE(trainX(:,4),predictionTrain(:,4)));

%% sensitivity analysis on number of hidden neurons
hiddenLayerSize    = 1:10:100;
trainR2   = zeros(size(hiddenLayerSize));
testR2   = zeros(size(hiddenLayerSize));
for i = 1 : numel(hiddenLayerSize)
    % create ELM for classification
    ELM = ELM_MatlabClass(nFeatures,hiddenLayerSize(i),activationFunction);
    % train ELM on the training dataset
    ELM = train(ELM,trainX,trainY);
    Yhat = predict(ELM,trainX);
    trainR2(i) = computeR2(trainX,Yhat);
    % validation of ELM model
    Yhat = predict(ELM,testX);
    testR2(i) = computeR2(testX,Yhat);
end

% plot results of accuracy with different sizes of the hidden layer
figure;
plot(hiddenLayerSize,[trainR2;testR2],'-o');
xlabel('Number of Hidden Neurons');
ylabel('R square error');
legend({'training','testing'},'Location','southeast');