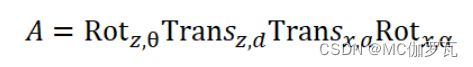机器人学-正运动学

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

文章目录

• 前言
• DH约定
• 正运动学
• 总结

---

前言

本文介绍串联机械臂基础算法，并使用python和matlab进行算法设计、建模仿真。

一、DH约定

标准DH配置

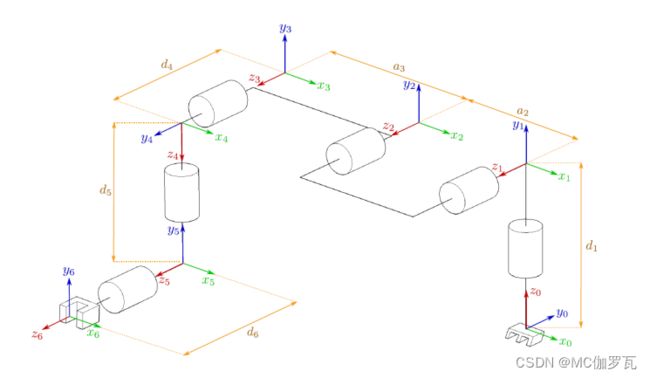
 坐标系示意图

 DH参数

二、正运动学

1.求解末端执行器矩阵

代码如下(python)：

import numpy as np
import math
"""
FR5的DH参数配置
Link i θi di ai αi
1         152   pi/2
2           -425
3           -395
4         130   pi/2
5         102   -pi/2
6         100
"""
def DH():
    A1 = np.array([[1,0,0,0],[0,0,-1,0],[0,1,0,152],[0,0,0,1]])
    A2 = np.array([[1,0,0,-425],[0,1,0,0],[0,0,1,0],[0,0,0,1]])
    A3 = np.array([[1,0,0,-395],[0,1,0,0],[0,0,1,0],[0,0,0,1]])
    A4 = np.array([[1,0,0,0],[0,0,-1,0],[0,1,0,130],[0,0,0,1]])
    A5 = np.array([[1,0,0,0],[0,0,-1,0],[0,1,0,102],[0,0,0,1]])
    A6 = np.array([[1,0,0,0],[0,0,-1,0],[0,1,0,100],[0,0,0,1]])
    T6 = np.dot(A1,np.dot(A2,np.dot(A3,np.dot(A4,np.dot(A5,A6)))))
    print("T6 = ",T6)

def InverseKinematics(x,y,z,rx,ry,rz):
    pass
def ForwardKinematics(j1,j2,j3,j4,j5,j6):
    pass

def distance(a,b,c):
    d=pow(a**2+b**2+c**2,1/2)
    return d

if __name__ == "__main__":
    x, y, z = input().split(",")
    d = distance(float(x), float(y), float(z))
    print("{:.2f}".format(d))
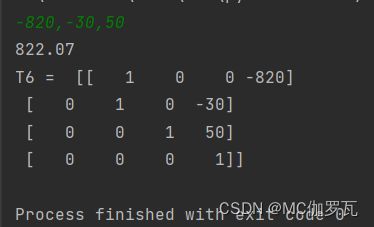
    DH()

末端执行器矩阵：

2.工作空间

代码如下(matlab)：

clear;
clc;
L(1) = Link('revolute','d',0.152,'a',0,'alpha',pi/2);
L(2) = Link('revolute','d',0,'a',-0.425,'alpha',0);
L(3) = Link('revolute','d',0,'a',-0.395,'alpha',0);
L(4) = Link('revolute','d',0.130,'a',0,'alpha',pi/2);
L(5) = Link('revolute','d',0.102,'a',0,'alpha',-pi/2);
L(6) = Link('revolute','d',0.100,'a',0,'alpha',0);
Five_dof = SerialLink(L,'name','6-dof');
Five_dof.base = transl(0,0,0);

L(1).qlim = [-179,179]/180*pi;
L(2).qlim = [-269,89]/180*pi;
L(3).qlim = [-162,162]/180*pi;
L(4).qlim = [-269,89]/180*pi;
L(5).qlim = [-179,179]/180*pi;
L(6).qlim = [-179,179]/180*pi;

num = 30000;

P = zeros(num,3);

for i = 1:num

    q1 = L(1).qlim(1) + rand*(L(1).qlim(2) - L(1).qlim(1));
    q2 = L(2).qlim(1) + rand*(L(2).qlim(2) - L(2).qlim(1));
    q3 = L(3).qlim(1) + rand*(L(3).qlim(2) - L(3).qlim(1));
    q4 = L(4).qlim(1) + rand*(L(4).qlim(2) - L(4).qlim(1));
    q5 = L(5).qlim(1) + rand*(L(5).qlim(2) - L(5).qlim(1));
    q6 = L(6).qlim(1) + rand*(L(6).qlim(2) - L(6).qlim(1));

    q = [q1 q2 q3 q4 q5 q6];

    T = Five_dof.fkine(q);

    P(i,:) = transl(T);

end

plot3(P(:,1),P(:,2),P(:,3),'b.','markersize',1);
% axis([-1.5 1.5 -1.5 1.5 -0.5 1.5])
hold on
grid on
daspect([1 1 1]);
view([45 45]);
Five_dof.plot([0 0 0 0 0 0])

%%

clf

hold on

axis([-1.5 1.5 -1.5 1.5 -1.5 2]);

for i = 1:num

    q1 = L(1).qlim(1) + rand*(L(1).qlim(2) - L(1).qlim(1));
    q2 = L(2).qlim(1) + rand*(L(2).qlim(2) - L(2).qlim(1));
    q3 = L(3).qlim(1) + rand*(L(3).qlim(2) - L(3).qlim(1));
    q4 = L(4).qlim(1) + rand*(L(4).qlim(2) - L(4).qlim(1));
    q5 = L(5).qlim(1) + rand*(L(5).qlim(2) - L(5).qlim(1));
    q6 = L(6).qlim(1) + rand*(L(6).qlim(2) - L(6).qlim(1));

    q = [q1 q2 q3 q4 q5 q6];

    T = Five_dof.fkine(q);

    Five_dof.plot(q);

    [x,y,z] = transl(T);

    plot3(x,y,z,'b.','markersize',1)
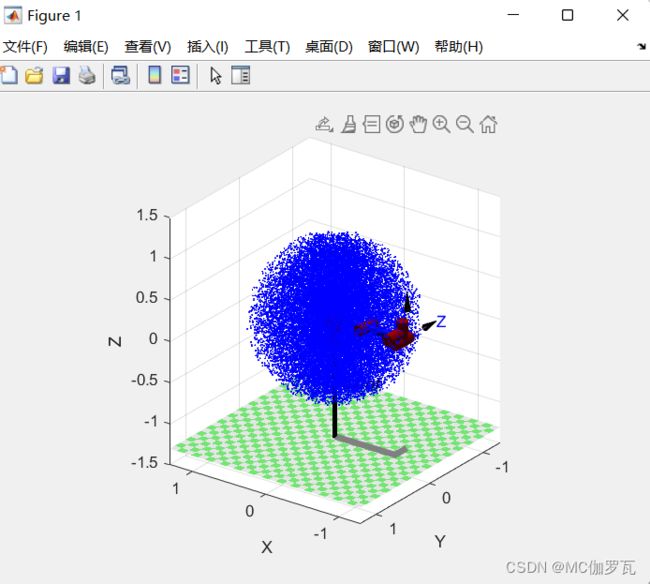
end

工作空间模型:

总结

以上就是今天要讲的内容，本文仅仅简单介绍了机器人正运动学基础算法实现。