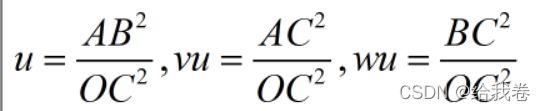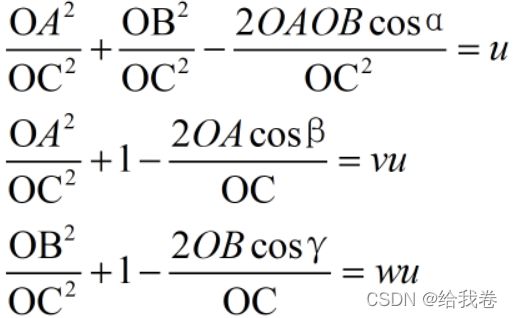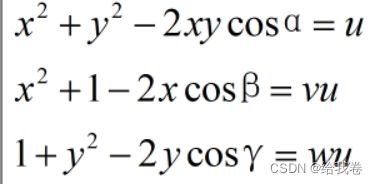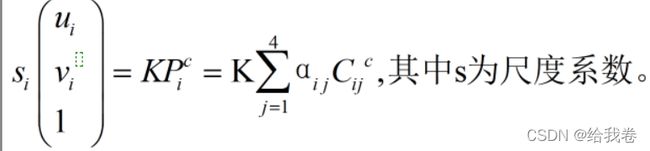位姿估计之PnP算法

        最近实验室学习安排是了解Pnp问题解法，于是就在网上找了各种文章学习，在此进行总结，给我卷！！！

1.什么是PnP问题？

        ​​​​​​PnP(全称Perspective-n-Points)，指3D到2D点对的物体运动定位问题，即已知物体在世界坐标系下的坐标，以及物体在相机的图像平面的像素坐标，求解相机的位姿（六个自由度，位置坐标和三个方向角）。

2.PnP问题的可解性

        知道了PnP问题后，就要讨论n在不同取值下的可解性了。

case1：

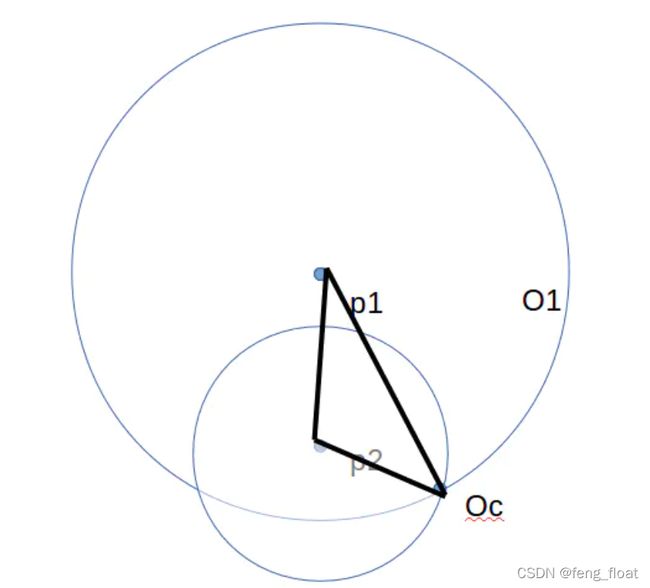
        n=1时，也就是特征点只有一个的时候，假设特征点为p1，相机光心为Oc，假设特征点在图像正中间，即p1Oc为相机z轴，此时相机可能在以特征点p1为圆心，半径任意的球上任意一点，这是有无数解的，图示如下：

        相机可能在球面O1、O2、O3上任意一点。

case2:

        n=2时，假设两个特征点分别为p1和p2，相机光心为Oc，已知p1和p2的世界坐标，则可知距离p1p2，又知特征点的像素坐标，以及相机内参，可求出∠p1Ocp2的余弦值（如何求后面会说明），利用小孔成像模型（相似三角形）可求出其中一条边Ocp1=r1，再利用余弦定理求出另一条边Ocp2=r2，然后分别以p1和p2为圆心，r1和r2为半径画球面，两个球面相交的地方就是相机可能的位置，此时仍有无数解，图示如下：

          两球面交界处是一片区域，相机可能在这片区域任意位置。

case3:

        n=3时，在原有的基础上又增加了一个球面，这时相机就位于三个球面的交界处，此时交界处有四个点，即相机位置有四个可能解，其中一个是最优解；

case4:

        n=4时，又增加了一个球面，暂时不考虑特殊情况，则四个球面相交于一点，即相机的位置。但由case3可知，在已知三个特征点的情况下，已经可以求出四个可能解，最优解就是四个解中的一个，而为了找出这个最优解又多找考虑一个特征点，对于计算效率方面是不划算的。基于此，通常实际应用中，我们选择用第四个特征点作为检验点，即分别从求出的四个可能解中计算出相机位姿，然后把第四个点经过重投影后计算误差，误差值最小（实际也不可能完全重合）的即为最优解。

        到此，PnP问题的可解性暂且讨论完毕。

3.PnP问题求解及数学推导

        3.1 DLT(Direct Linear Tranform，直接线性变换)

                设一个空间特征点的世界坐标为Pw(X，Y，Z)，其对应的像素坐标为p(u，v)，列一下当前的条件，已知相机内参K（通过相机标定求得，而且内参不会随着物体运动而变），要求的是旋转矩阵R和平移矩阵t，有世界坐标->像素坐标转化可列如下方程（为了能表示为矩阵相乘的形式，简化运算，都转化为齐次坐标）：           

               

我上面写的这个公式忽略了尺度系数，其实它和内参K一样，后面都会被消去，这里提醒大家注意。

等号两边左乘K逆，同时定义变换矩阵T=[R|t],展开如下：

把K逆用第三行表示，代入前两行化简得到两个约束：

 这里，定义变换矩阵T的行向量：

则上述两个约束方程可化为：

 

未知量是Tt，其它已知，一个特征点提供两个方程， 若有n个特征点，则方程如下：

变换矩阵有12个参数，因此需要至少6对特征匹配点才能求出线性解，同时，若n>6时，方程数大于未知数，方程属于超定方程，可以利用SVD分解使用最小二乘法寻找近似最优解，求解过程暂不列出（有点复杂）参考如下：最小二乘法求解相机位姿。

 

 3.2 P3P

         已知空间中三个特征点，根据小孔成像模型可以简单表示如下： 

                         

        图中A、B、C三点为空间特征点，在成像平面的对应投影点分别为a、b、c，O为相机光心，先讨论一下已知条件，A、B、C三点世界坐标已知，则可求出AB、BC、AC；a、b、c为像素坐标，也可求出ab、ac、bc，除此之外还能求出图中不易看出的∠aOb=α，∠aOc=β，∠bOc=γ的余弦值，至于如何求放到后面，先假设它们已知。

        我们目的是什么呢？相机的位姿，也就是R和t，怎么求？很简单，就是先求出A、B、C三点在相机坐标系下的坐标，然后世界坐标->相机坐标的转换，即经过旋转R和平移t。这里我们可以看出3D-2D的点对运动问题被转化成了3D-3D的刚体变换，之后通过ICP(Iterative Closest Point)迭代最近点算法求解。之后可以看到EPnP求解也是3D->3D。

        从上图中找出AOB、AOC、BOC，利用高中学的余弦定理得：

        

        方程左右两边同时除以 ，得：

         

        对上述方程进行变形，令

        

        其中

         

        显然v、w已知，u未知，代入上述方程，得：

        

        继续化简变形，令 

        

        代入上述方程得：

        

        此时方程中x,y,u未知，为了减少未知数个数，我们把方程2和3中等号右边的未知数u用方程1等号左边表示，化简得：

         至此，两个方程，两个未知数x、y，形式比较简便。可以看到方程是二元二次方程，网上说可以使用吴零点分解法求（具体不清楚），有兴趣的可以去看相关论文。

        这里假设经过求解得到了x、y，然后求出了OA、OB、OC的值，进而可求出A、B、C三点在相机坐标系下的坐标，接下来就是3D->3D的刚体变换了（旋转+平移就搞定了）。

        关于如何求∠aOb=α，∠aOc=β，∠bOc=γ的余弦值，我也简单写一下，如图：

∠AOB=α，p为成像平面中心，在相机的光轴上，也就是Op⊥成像平面，a、b、c为空间点投影点，坐标已知，因此可直接求出ap、bp、cp的长度，op=f，f为相机内参，由相机标定求得，可利用勾股定理求出Oa、Ob、Oc的长度，故Oab、Oac、Obc的三边长度就知道了，因而α、β、γ的余弦值用余弦定理就可以得到。

 

3.3 EPnP

        先说一下大体思路：在空间中选择4个控制点（相当于基点，用来表示其它点），然后把空间中的其他参考点用这四个控制点表示，得到四个控制点的加权系数，四个加权系数组成了质心坐标（小白认为：这里得到的质心坐标是EPnP的关键，因为得到了一个约束条件，α为加权系数，n=4），然后求控制点在相机坐标下的坐标，最后就是3D-3D求解相机位姿R和t的问题了。

        设空间中的参考点为i=1,2,..,n， 4个控制点，i=1,2,3,4。

可得到下面的关系式：

        ，

        其中α为质心坐标，如果不了解，可以参考：https://blog.csdn.net/weixin_33204399/article/details/104121072

         同样相机坐标系也满足上述关系：

        

        则相机坐标与的关系可表示如下：

         设参考点对应的图像上的投影点为，则相机坐标->像素坐标的转化如下：

 其中

代入上式得：

从中可得到三个方程：

消去s得到两个方程：

 n个参考点联立，就能得到线性方程组：

其中 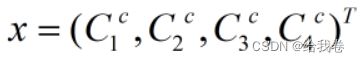，解出x，即得到控制点在相机坐标系下得坐标，3D-3D求解位姿R和T喽。

3.4 非线性优化

        上面的方法都是线性的，还可以把PnP问题构建为一个关于重投影误差的非线性最小二乘问题。线性方法往往是通过将空间点的位置看做已知量，通过构建方程组求解相机位姿。而非线性优化则将相机位姿和空间点位置都看成优化变量，放在一起优化。这种方法将相机位姿和三维点位置放在一起进行重投影误差最小化的优化，是一种整体的优化方法。

        具体的优化原理请参考:

https://blog.csdn.net/qq_37394634/article/details/104430656

4.总结一下

        对比以上几种方法，DLT先求出变换矩阵T=[R|t]，未考虑R正交矩阵的约束，精度不足，需要六个特征点，计算量大；P3P利用了三个特征点，速度较快，但是正因为其仅仅利用了三个点，存在误匹配点时，就会得到误差较大的结果，精度也不行；而EPnP则可以利用多个点，即使存在误匹配，影响也会较低，得到的结果可靠性高；而对于非线性优化，其精度应该是最高的，但是其计算量很大，实时性比较差，当然，随着技术不断迭代发展，其实时性也在不断上升。到此，就结束了，溜了。