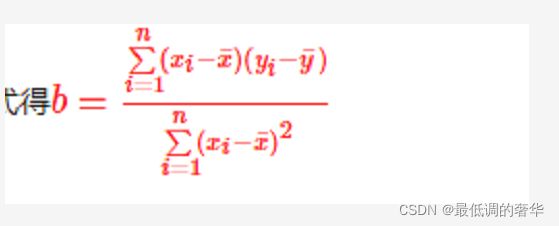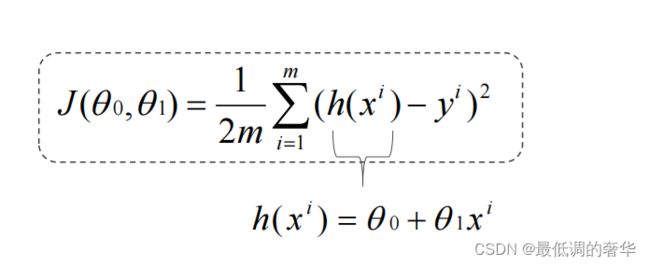最小二乘法,梯度下降法,sklearn中API来实现线性回归
- 导入模块
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
1.最小二乘法来实现线性回归
1.导入训练集数据
x = np.array([0.86, 0.96, 1.12, 1.35, 1.55, 1.63, 1.71, 1.78])
y = np.array([12, 15, 20, 35, 48, 51, 59, 66])
def fit(x,y):
if len(x) != len(y):
return
numerator = 0.0
denominator = 0.0
x_mean = np.mean(x)
y_mean = np.mean(y)
for i in range(len(x)):
numerator += (x[i]-x_mean)*(y[i]-y_mean)
denominator += np.square((x[i]-x_mean))
b0 = numerator / denominator
b1 = y_mean-b0*x_mean
return b0,b1
def predit(x,b0,b1):
return b0*x+b1
b0,b1 = fit(x,y)
2.预测
x_test = np.array([0.75, 1.08, 1.26, 1.51, 1.6, 1.67, 1.85])
y_test = np.array([10, 17, 27, 41, 50, 64, 75])
y_predit = predit(x_test,b0,b1)
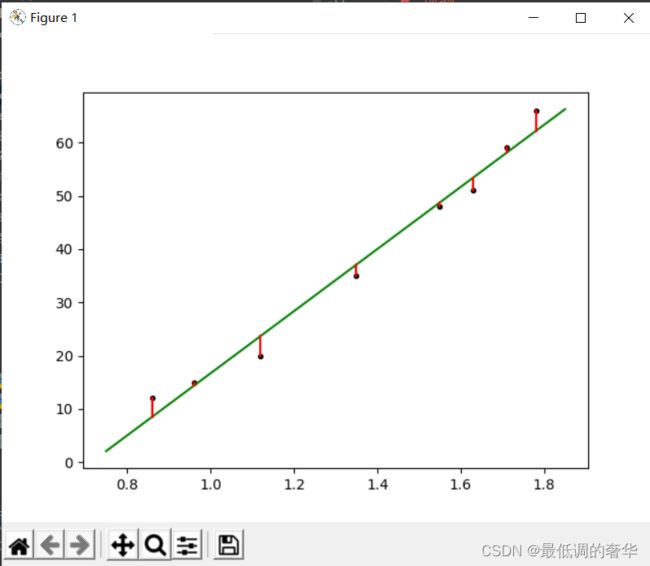
3.绘制图像
plt.plot(x, y, 'k.')
plt.plot(x_test, y_predit, 'g-')
yr = predit(x, b0, b1)
print(yr)
for idx, x in enumerate(x):
plt.plot([x, x], [y[idx], yr[idx]], 'r-')
# print([x, x],[y[idx], yr[idx]])
plt.show()
2.梯度下降法来实现线性回归
链接:https://pan.baidu.com/s/19GqEedcXjkoPUjqVhXobsA
提取码:0812
- data数据的网盘文件
import numpy as np
import matplotlib.pyplot as plt
# 读取数据
data = np.loadtxt(r"F:\ev播放器数据分析学习\data(2).csv", delimiter=',')
print(data)
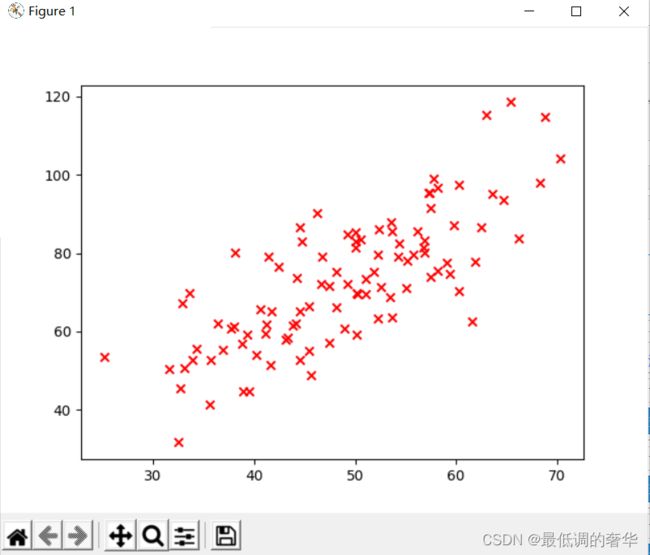
# 查看数据分布 可视化
x_data = data[:, 0]
y_data = data[:, 1]
plt.scatter(x_data, y_data, color="red", marker='x')
plt.show()
# 一元线性回归
# 梯度下降法
# 初始化学习率 (步长)
learning_rate = 0.0001
# 初始化截距
b = 0
# 初始化斜率
k = 0
# 初始化最大迭代次数
n_iterables = 50
def compute_mse(b, k, x_data, y_data):
"""
计算代价函数 --- MSE
-误差和:循环len(x_data)次,取出来每个样本的误差
:param b:
:param k:
:param x_data:
:param y_data:
:return: MSE
"""
# 初始化误差和
total_error = 0
# 循环
for i in range(len(x_data)):
total_error += (y_data[i] - (k * x_data[i] + b)) ** 2
# 均方误差 = 误差和/样本个数
# 便于求导 :乘以1/2
mse_ = total_error / len(x_data) / 2
return mse_
- 2.梯度下降法
def gradient_descent(x_data, y_data, b, k, learning_rate, n_iterables):
"""
梯度下降
- 不断对损失函数求导(斜率),使得θ不断的迭代到损失函数最小
"""
# 计算总样本数量
m = len(x_data)
# 循环---- 迭代次数
for i in range(n_iterables):
# 初始化b偏导
b_grad = 0
# 初始化k偏导
k_grad = 0
# 计算偏导的总和在求平均
# 遍历m次
for j in range(m):
# 对k,b求偏导
b_grad += (1 / m) * (k * x_data[j] + b - y_data[j])
k_grad += (1 / m) * (k * x_data[j] + b - y_data[j]) * x_data[j]
# 更新k,b
b = b - (learning_rate * b_grad)
k = k - (learning_rate * k_grad)
# 每迭代5次输出一次图形
if i % 5 == 0:
print(f'当前第{i}迭代')
# 绘制散点图
plt.scatter(x_data, y_data, color="maroon", marker='x')
# 绘制预测图
plt.plot(x_data,k*x_data+b)
plt.show()
J = compute_mse(b,k,x_data,y_data)
return b,k
print(f"开始:截距b={b},斜率k={k},损失={compute_mse(b,k,x_data,y_data)}")
print("开始迭代")
b,k = gradient_descent(x_data,y_data,b,k,learning_rate,n_iterables)
print(f"迭代{n_iterables}次后:截距b={b},斜率k={k},损失={compute_mse(b,k,x_data,y_data)}")
3.sklearn中API实现线性回归
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
# 读取数据
data = np.loadtxt(r"F:\ev播放器数据分析学习\data(2).csv", delimiter=',')
print(data)
# 查看数据分布 可视化
# 一维变为二维
x_data = data[:, 0,np.newaxis]
y_data = data[:, 1]
plt.scatter(x_data, y_data, color="red", marker='x')
# plt.show()
# 创建模型
model = LinearRegression()
# 训练
model.fit(x_data,y_data)
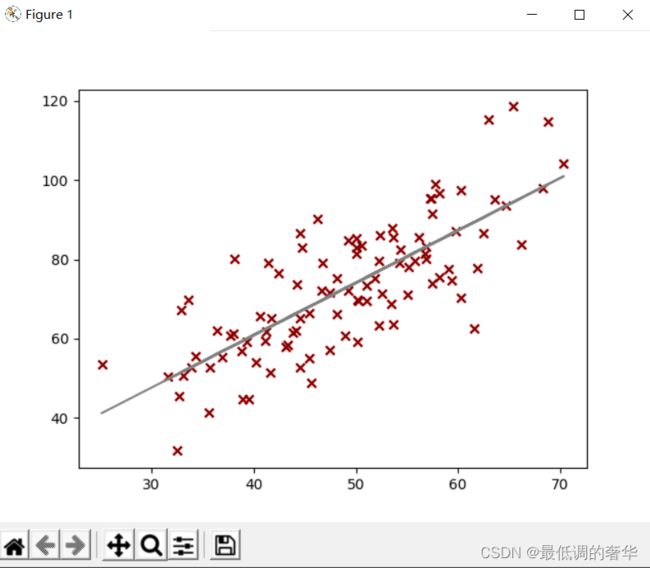
# 绘制散点图
plt.scatter(x_data, y_data, color="maroon", marker='x')
# 绘制预测图
plt.plot(x_data, model.predict(x_data), 'gray')
plt.show()