数学模型——基于差分方程的减肥模型（基于python）
背景
目前，比较标准的评测体重的标准就是BMI指数，它等于体重除以身高的平方。我国的参考标准认为，BMI指数小于18.5即为偏瘦，在18.5至23.9为正常，在24至27.9之间为超重，大于28即为肥胖。
在正常情况下，人体通过食物摄入的热量与代谢和运动消耗的热量大致上是平衡的，于是体重基本保持不变，而当能量守恒被打破时就会引起体重变化。
减肥计划以减少摄入热量，增加运动量的方法进行考虑
模型假设
1.体重增加正比于吸收的热量，平均每8000kcal增加体重1kg
2.身体正常代谢引起的体重减少正比于体重，每周每千克体重消耗热量一般在200kcal至320kcal之间，且因人而异，这相当于体重70kg的人每天消耗2000kcal至3200kcal
3.运动引起的体重减少正比于体重，且与运动形式和运动时间有关
4.为了安全与健康，每周吸收热量最好不要小于10000kcal，且每周减少量不要超过1000kcal，每周体重减少不要超过1.5kg
| 运动 | foot | run | dance | pingpang | bicycle | swim |
|---|---|---|---|---|---|---|
| 热量消耗 | 3.1 | 7.0 | 3.0 | 4.4 | 2.5 | 7.0 |
注：数据仅供参考
基本模型
记第k周（初）体重为w(k)(kg)，第k周吸收热量为c(k)(kcal)，k=1，2...。设热量转换系数为α。深体代谢消耗系数为β，根据模型假设，正常情况下（不考虑运动）体重变化的基本方程为(只要能表示这段方程，主体部分基本就完事，使用一个while循环或者for循环即可）
根据假设1，
，当确定一个人的代谢消耗系数β后，就可按照上述式子由每周吸收的热量c(k)推到ta体重w(k)的变化，增加运动时，需要更改消耗系数β值，具体会在下面给出
实例
某人身高1米7，体重100kg，BMI高达34.6，已知每周吸收20000kcal热量，体重长期未变，目标是需要将ta体重降至75kg，并维持下去。
此时设置一个两阶段计划，第一阶段将吸收热量由20000kcal减至10000kcal；第二阶段保持吸收热量，直至达到减肥目标（亦或者为了加快进程增加运动）
故，根据上述信息，可以得出以下信息：
根据第一阶段要求，吸收热量要降至10000，故得出c(k)
此时，带入基本模型，就可以得到关于体重的差分方程
以w(1)=100kg为初始值，按照以上式子进行编程，得出11周初体重为93.616kg
代码实现
定义一个loseplan函数，用于制定计划，以及显示每周的体重变化，当然，首先判定BMI指数是否过大。参数为体重，身高，摄入热量，每周默认减少热量为1000kcal，设置了sport，即运动下的第二阶段体重变化
def losePlan(weight,height,c,lose=1000,sport=False,category='跳舞'):
bmi = round(weight/height**2)
if bmi > 26:
goalw = 26 * height ** 2
print('您目前体重指数为{}，属于超重范围，正在为您计算第一阶段减食计划所用时间'.format(bmi))
print('您的目标体重为{}'.format(round(goalw, 2)))其次，α是给定已知且不会变化的，β是根据每个人的不同有差异的
a = 1 / 8000 # 热量转换系数
beta = a * c / weight # 代谢消耗系数接下来进入差分方程的阶段，我使用的是while循环进行差分，使用for循环的话，我认为需要先算出时间，再进行，whlie循环不会。故定义一个time获取一共需要多少周才能完成第一阶段
time = 0
while c != 10000:
c = c - lose
time += 1
weight = weight * (1 - beta) + a * (20000 - 1000 * time)
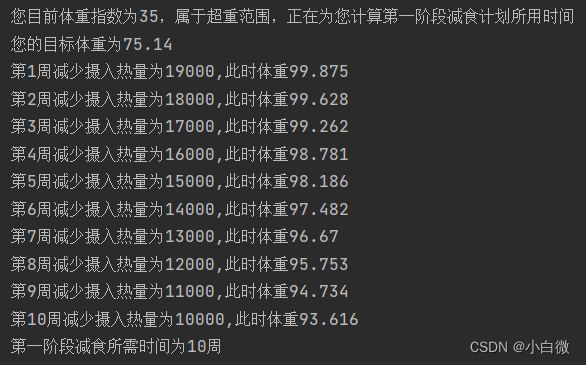
print('第{}周减少摄入热量为{},此时体重{}'.format(time,c,round(weight, 3)))
print('第一阶段减食所需时间为{}周'.format(time))此时将参数写上，运行代码，可以获得第一阶段每一周体重的变化，如下图
第二阶段
不运动的情况下，要求每周热量标尺下限10000kcal，故此时方程为
当体重减至75.14kg或以下时，第二阶段结束
若想加快进程，需要增加运动，根据前面运动消耗表，记热量消耗为γ，每周运动t小时，则基本模型中β改为β+αγt，此时方程为
设运动方式为跑步，每周8小时（实际上谁跑那么久呀。。。）
if sport:
sport_cate = {'foot': 3.1, 'run': 7.0, 'dance': 3.0,
'pq': 4.4, 'bicycle': 2.5, 'swim': 7.9}
for i in sport_cate.keys():
if category == i:
s = sport_cate[category]
while weight > 75:
weight = weight + a * c - weight * (beta + a * s * 8)
time += 1
print("第{}周的体重为{}".format(time, round(weight, 3)))
# 假设不运动
else:
while weight >= 75:
a = 1 / 8000
weight = weight * 0.975 + a * c
time += 1
print("第{}周的体重为{}".format(time, round(weight, 3)))
当不运动时，有代码得出结果，还需要22周才能达到目标体重，若是进行运动，则需要15周。
完整代码
def losePlan(weight,height,c,lose=1000,sport=False,category='跳舞'):
bmi = round(weight/height**2)
if bmi > 26:
goalw = 26 * height ** 2
print('您目前体重指数为{}，属于超重范围，正在为您计算第一阶段减食计划所用时间'.format(bmi))
print('您的目标体重为{}'.format(round(goalw, 2)))
a = 1 / 8000 # 热量转换系数
beta = a * c / weight # 代谢消耗系数
time = 0
while c != 10000:
c = c - lose
time += 1
weight = weight * (1 - beta) + a * (20000 - 1000 * time)
print('第{}周减少摄入热量为{},此时体重{}'.format(time,c,round(weight, 3)))
print('第一阶段减食所需时间为{}周'.format(time))
if sport:
sport_cate = {'foot': 3.1, 'run': 7.0, 'dance': 3.0, 'pq': 4.4, 'bicycle': 2.5, 'swim': 7.9}
for i in sport_cate.keys():
if category == i:
s = sport_cate[category]
while weight > 75:
# weight = weight + a * c - weight * (beta + a * s * 8)
weight = 0.97*weight + 1.25
time += 1
print("第{}周的体重为{}".format(time, round(weight, 3)))
# 假设不运动
else:
while weight >= 75:
a = 1 / 8000
weight = weight * 0.975 + a * c
time += 1
print("第{}周的体重为{}".format(time, round(weight, 3)))
else:
print('您的体重指数为{}，体重正常'.format(bmi))
if __name__ == '__main__':
weight = 100
height = 1.7
c = 20000
name = 'run'
losePlan(weight,height,c,sport=True,category=name)
总结
代码不是很长，但是足够用。后期我在进行整理时，发现若是从第一阶段开始运动，会更好，而原书中也是这样表达，我没注意到，所以代码部分，只有第二阶段不运动的情况下是比较正确的。
若是小伙伴们对代码有什么疑惑，可以私信或评论区发表意见哈
参考书目：姜启源 谢金星 叶俊.数学模型（第五版）