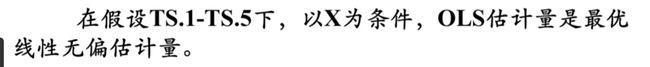UESTC 计量经济学复习
第一章 回归分析概述
计量经济学研究路线
- 建立理论模型
- 确立计量经济学模型
- 搜集检查并整理
数据 - 估计计量经济学模型
- 评价计量经济学模型
- 应用计量经济学模型
回归分析的现代含义
回归分析是关于研究一个叫做因变量的变量(Y)对另一个或多个叫做自变量的变量(X)的依赖关系
其用意在于通过自变量在重复抽样中的已知或设定值,去估计或预测因变量的总体均值
确定关系:确定变量之间的函数关系
统计关系:随机变量之间的依赖关系
计量经济学关注的是统计关系
线性的含义
有两种线性,变量线性和参数线性
线性回归是指对估计参数为线性的一种回归(即估计参数只以一次方出现),对自变量X则可以是或不是线性的
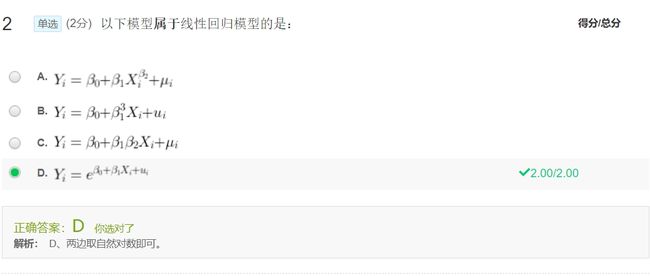
判断下列方程是不是线性回归?
E ( Y ∣ X i ) = β 0 + β 1 2 X i E(Y|X_i)=\beta_0+\beta_1^2 X_i E(Y∣Xi)=β0+β12Xi 不是线性回归
E ( Y ∣ X i ) = β 0 + β 1 X 1 X 2 E(Y|X_i)=\beta_0+\beta_1 X_1 X_2 E(Y∣Xi)=β0+β1X1X2 是线性回归
随机干扰项 ε i = Y i − E ( Y i ∣ X i ) \varepsilon_i=Y_i-E(Y_i|X_i) εi=Yi−E(Yi∣Xi)
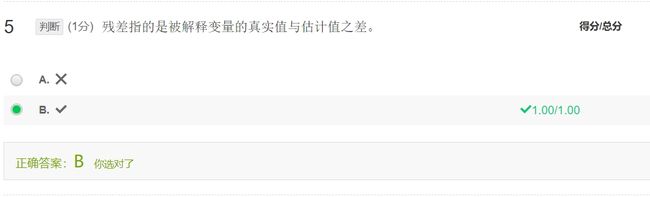
残差 ε i ^ = e i = Y i − Y i ^ \hat{\varepsilon_i}=e_i=Y_i-\hat{Y_i} εi^=ei=Yi−Yi^
小结
- 计量经济学,从字面意思来上讲,叫"经济度量",属于经济学的一个分支学科,主要致力于量化理论关系。回归分析虽然仅仅是计量经济学分析方法的一种,确实目前最常用的一种方法。
- 计量经济学最主要的用途为:描述经济关系、假设检验和预测。根据研究的需要,特定的计量经济学方法会有所不同。
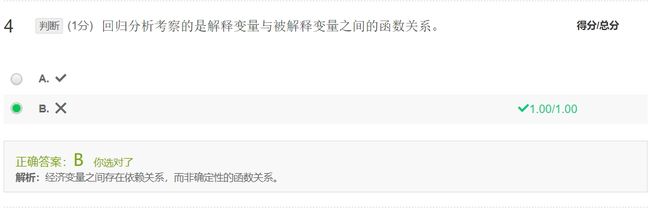
- 尽管回归分析设定被解释变量是一个或者多个解释变量的函数,但回归分析本身并不能证明或隐含因果关系。
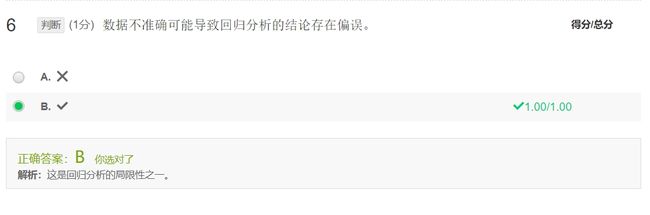
- 回归方程中必须加入随机误差项,用于度量被解释变量没有完全被解释变量解释而形成的误差。随机误差项的组成部分有:①遗漏或者省略变量;② 数据的测量误差;③隐含理论的函数形式与回归方程不同; ④纯随机误差或不可预知的事件。
- 估计出的回归方程式真实回归方程的近似代替,是从包含X和Y的样本数据中计算出来的。由于真实回归方程不可知,所以,计量经济分析注重的是估计出的回归方程和回归参数的参数估计值。被解释的变量的特定观测值与其估计值之差成为残差。
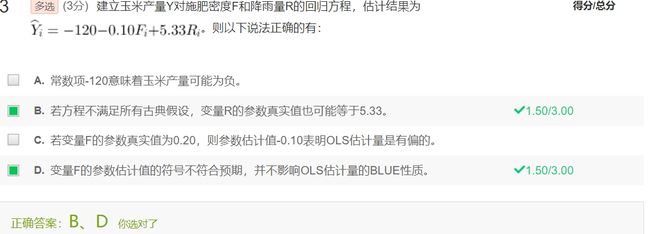
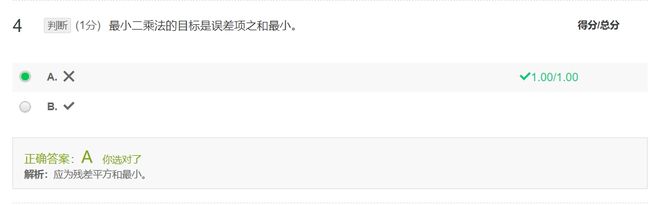
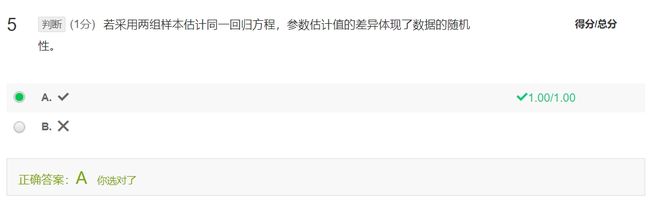
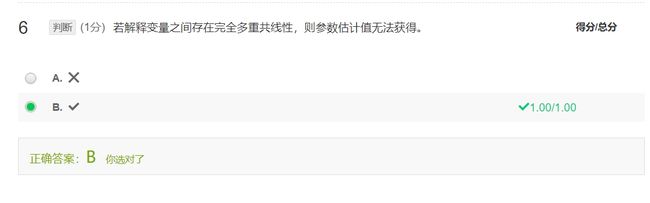
例题
第二章 最小二乘法
偏回归系数:当其他变量相同(保持其他变量不变)时,特定变量对被解释变量的边际影响(贡献)
n为样本量,k为待估计参数数量,通常情况下 n ≥ 5 ∗ k n \geq 5*k n≥5∗k
最小二乘法估计量$ \hat{\beta} $是确定性变量还是随机变量?为什么?
β ^ \hat{\beta} β^是由Y计算来的,Y是一个随机变量,随机性来自随机干扰项 ε \varepsilon ε, ε \varepsilon ε影响Y,Y影响 β ^ \hat{\beta} β^,所以 β ^ \hat{\beta} β^是一个随机变量,同时如果Y服从正态分布,那么$ \hat{\beta} $也服从正态分布
判断估计量优劣的标准是什么?
- 估计值的均值是否等于真实值:无偏性
- 估计量的方差是否足够小:有效性
- 估计量的极限是否趋于真实值:一致性
控制变量的选择
去什么,加什么,因为我们的被解释变量受到多个因素的影响,仅仅用一元线性回归是不够的,以餐厅收入案例为例,虽然我们关心的是居民收入对于餐厅收入的影响,但我们考虑到竞争对手的数量还有人口密度等等会影响餐厅收入,如果不把这两个影响因素去掉,可能得不到真实的回归结果,为了去除这两个因素的影响,我们要把这两个变量加入道方程中去。
古典假设:
- 回归模型是线性的,模型设定无误且含有误差项。
- 误差项的总体均值为0。
- 所有解释变量与误差项都不相关
- 误差项观测值互不相关(不存在序列相关性)
- 误差项具有同方差(不存在异方差性)
- 任何一个解释变量都不是其他解释变量的完全线性函数(不存在多重共线性)
- 误差项服从正态分布(该假设是选择性的,但通常被采用)
古典假设小结
- 7个古典假设表述为:回归模型是线性的且含有一个均值为0且与解释变量不相关的误差项;各误差项观测值之间不想管;误差项观测值之间互补相关;误差项的方差相同,服从正态分布(不要求);另外,解释变量之间一定不能相互存在完全的线性函数关系。
- 估计量的两个最重要的性质是无偏性和最小方差性。无偏估计量是指被估计参数的期望与真实值相等的估计量。在给定的一类估计量中(例如无偏估计量),茹估计值分布的方差在所有估计量中最小时,则满足最小方差性。
- 在古典假设下,普通最小二乘估计量被证明具有最小方差性,线性,无偏性(或称BLUE,即最优线性无偏估计量),即高斯——马尔科夫定理。当一个或多个古典假设不成立时(正态分布假设除外),在某些时候,尽管普通最小二乘法仍然能够提供比随后章节中所讨论的其他可供选择估计的方法得到的更好的估计量,但普通最小二乘估计量不再是BLUE的。
- 因为 β k ^ \hat{\beta_k} βk^的普通最小二乘估计量的抽样分布是BLUE的,所以 β k ^ \hat{\beta_k} βk^具有令人满意的性质。另外,随着被观测样本数量的增加, β k ^ \hat{\beta_k} βk^的抽样分布中的方差(或离散程度)减小。
- 计量经济学中有一套标准的记述符号,如下表所示
| 总体参数 | (真实值,但不能观测) |
|---|---|
| 回归参数 | β k \beta_k βk |
| 参数估计量的期望 | E ( β k ^ ) E(\hat{\beta_k}) E(βk^) |
| 误差项的方差 | σ 2 或 V A R ( ε i ) \sigma^2 或 VAR(\varepsilon_i) σ2或VAR(εi) |
| 误差项标准差 | σ \sigma σ |
| 参数估计量的方差 | σ 2 ( β k ^ ) \sigma^2(\hat{\beta_k}) σ2(βk^) 或 V A R ( β k ^ ) VAR(\hat{\beta_k}) VAR(βk^) |
| 参数估计量的标准差 | σ β k ^ \sigma_{\hat{\beta_k}} σβk^ 或 σ ( β k ^ ) \sigma(\hat{\beta_k}) σ(βk^) |
| 误差项或随机干扰项 | ε i \varepsilon_i εi |
| 估计值 | (由样本观测得到) |
|---|---|
| 回归参数估计值 | β k ^ \hat{\beta_k} βk^ |
| 误差项的方差的估计值 | s 2 或 V A R ( σ 2 ) s^2 或 VAR(\sigma^2) s2或VAR(σ2) |
| 误差项标准差的估计值 | s s s 或 S E SE SE |
| 参数估计量的方差估计值 | s 2 ( β k ^ ) s^2(\hat{\beta_k}) s2(βk^) 或 V A R ^ ( β k ^ ) \widehat{VAR}(\hat{\beta_k}) VAR (βk^) |
| 参数估计量的标准差估计值 | σ β k ^ ^ \hat{\sigma_{\hat{\beta_k}}} σβk^^ 或 S E ( β k ^ ) SE(\hat{\beta_k}) SE(βk^) |
| 残差项 | e i e_i ei |
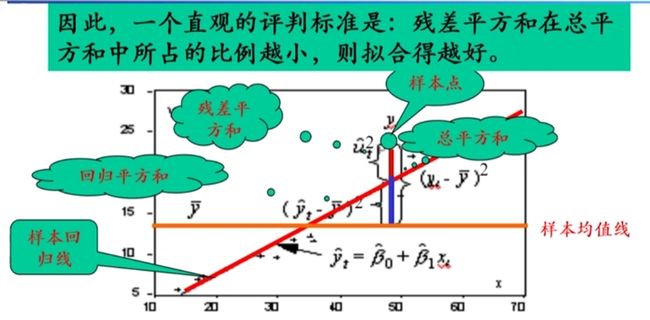
拟合优度
OLS估计量是BLUE(最小方差性[有效性],线性,无偏性),但采用OLS不一定能够得到满意的结果
从几何意义上说,拟合优度是指样本回归线对样本数据拟合得多好
判定系数 ( R 2 ) (R^2) (R2)
R 2 = 回 归 平 方 和 总 平 方 和 = E S S T S S = 1 − R S S T S S < 1 R^2=\frac{回归平方和}{总平方和}=\frac{ESS}{TSS}=1-\frac{RSS}{TSS} < 1 R2=总平方和回归平方和=TSSESS=1−TSSRSS<1
一般来说, ( R 2 ) (R^2) (R2)的值越接近1,表明拟合优度越好;相反,越接近0,意味着回归估计方程不能比样本均值 Y ˉ \bar{Y} Yˉ更好的解释 Y i Y_i Yi的值
判定系数 ( R 2 ) (R^2) (R2)是解释变量个数的非减函数,即增加解释变量, ( R 2 ) (R^2) (R2)会增加或不变
( R 2 ) (R^2) (R2)不是越大模型越好
- 增加无关的解释变量,使模型失去经济含义
- 降低
自由度,降低参数估计量的可靠性
自由度:观测样本数 减去待估参数的个数
调整的判定系数
对参数(包括截距项)的个数k进行惩罚,在模型拟合优度(好)与其复杂性(不好)之间进行权衡
R 2 ˉ = 1 − ∑ e i 2 / ( n − k ) ∑ y i 2 / ( n − 1 ) = 1 − ( 1 − R 2 ) n − 1 n − k \bar{R^2}=1-\frac{\sum e_i^2/(n-k)}{\sum y_i^2/(n-1)}=1-(1-R^2)\frac{n-1}{n-k} R2ˉ=1−∑yi2/(n−1)∑ei2/(n−k)=1−(1−R2)n−kn−1
当模型中新增解释变量时, R 2 ˉ \bar{R^2} R2ˉ变化的方向(上升、下降或者不变)依赖于新变量对回归拟合的贡献是否超过对损失一个额外自由度所作修正的补偿
- 拟合优度仅是衡量回归总体质量的指标之一
- 参数估计值符合经济理论的程度、研究者对参数预期比拟合优度更加重要
小结
- 普通最小二乘法是利用一组数据求的回归参数估计值的最常用的方法。普通最小二乘法使得一个特定样本的残差平方和( ∑ e i 2 \sum e_ i^2 ∑ei2)最小。
- 调整的判定系数 R 2 ˉ \bar{R^2} R2ˉ是经过自由度调整后的判定系数,他衡量了Y与他的均值被特定回归方程解释的比例。方程中新增加一个变量时,只有拟合有毒提高的程度超过了自由度下降的损失,调整的判定系数 R 2 ˉ \bar{R^2} R2ˉ才会更大,所以,多数研究者在评价回归方程的拟合优度时,都自然地使用调整地判定系数 R 2 ˉ \bar{R^2} R2ˉ
- 切记,估计方程地拟合有毒只是一个衡量回归整体质量地指标之一。许多其他的标准,包括参数估计值与经济理论地一致性,以及与预期(研究者在搜集数据前做出地预期)的一致性,都比调整的判定系数 R 2 ˉ \bar{R^2} R2ˉ更重要。
例题
第三章 假设检验
假设检验的基本原理
我们用样本的信息来检验总体的信息
假设检验:先对总体的特征作出某种假设,然后通过抽样研究的统计推理,对此假设应该拒绝还是被接受做出推断
基本思想:小概率原理、反证法
原假设( H 0 H_0 H0) 备择假设( H A H_A HA)
因为拒绝假设比较简单,我们只需要举出一个反例,而接受一个假设相对比较困难,因为我们可能需要穷举所有的情况
因此我们就可以根据研究者预期来设计假设,我们将希望出现的结果作为备择假设,将不希望出现的结果作为原假设
如果回归分析希望出现一个正的参数 β \beta β,原假设和备择假设应该为:
H 0 : β ≤ 0 ; H A : β > 0 H_0:\beta \leq 0; H_A: \beta > 0 H0:β≤0;HA:β>0
单侧检验:具有明显的预期
如果回归分析希望参数 β \beta β不为零,原假设和备择假设应该设为:
H 0 : β = 0 ; H A : β ≠ 0 H_0: \beta = 0; H_A: \beta \ne 0 H0:β=0;HA:β=0
双侧检验: 预期不确定
假设检验是要确定一个标准(判定准则),以便决定拒绝或不拒绝某个原假设 H 0 H_0 H0
当拒绝原假设时,通常表述为统计上显著;反之,统计上不显著
两类错误
| H 0 H_0 H0为真 | H 0 H_0 H0不为真 | |
|---|---|---|
| 拒绝 H 0 H_0 H0 | 第一类错误(弃真) | 正确 |
| 不拒绝 H 0 H_0 H0 | 正确 | 第二类错误(纳伪) |
犯第一类错误的概率: P ( H A ∣ H 0 ) = α P(H_A|H_0)=\alpha P(HA∣H0)=α
犯第二类错误的概率: P ( H 0 ∣ H A ) = β P(H_0|H_A)=\beta P(H0∣HA)=β
α \alpha α 越大 β \beta β越小,我们主要关注第一类错误出现的概率 α \alpha α
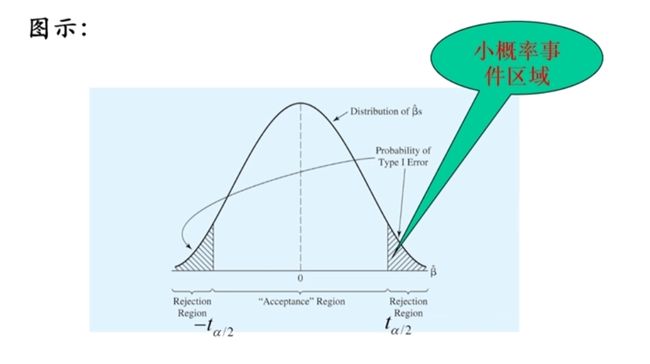
假设检验的判定准则
- 判定准则是比较样本统计量与预先设定的临界值之间的大小
- 参数估计值范围分为两个区域:拒绝域和“接受域”
假设检验的方法
置信区间法
根据参数估计量的分布,在给定的置信水平(如95%)下,构造一个随机置信区间;若该随机区间覆盖原假设值,则不拒绝原假设,否则拒绝原假设
置信区间的构造
首先设定显著性水平(第一类错误的概率) α \alpha α,然后确定一个正数 δ \delta δ,使得随机区间 ( β ^ − δ , β ^ + δ ) (\hat{\beta}- \delta, \hat{\beta}+ \delta) (β^−δ,β^+δ)包括参数真实值 β \beta β的概率为 1 − α 1-\alpha 1−α(置信水平)
P ( β ^ − δ ≤ β ≤ β ^ + δ ) = 1 − α P(\hat{\beta}- \delta \leq \beta \leq \hat{\beta}+ \delta)=1-\alpha P(β^−δ≤β≤β^+δ)=1−α
显著性假设法
显著性检验法直接比较参数估计值和原假设之间的差异大小。若"差异" 较大,则拒绝原假设;反之,不拒绝原假设
怎样判断差异的大小
判断 β ^ − β 0 \hat{\beta}-\beta_0 β^−β0是否显著异于0的关键在于构造一个函数f( β ^ − β 0 \hat{\beta}-\beta_0 β^−β0)(称为统计量),该统计量具有确定的分布规律;比较该统计量的值与分布临界值来判断差异是否显著
如果得到的P值小于我们要求的显著性水平(5%)的话,我们就拒绝原假设,反之,不拒绝。
t检验
检验单个变量对被解释变量是否由解释力
t = β ^ − β 0 s e ( β ^ ) t=\frac{\hat{\beta}-\beta_0}{se(\hat{\beta})} t=se(β^)β^−β0
单侧T检验的判定方法
- 根据t值判断,如果 ∣ t k ∣ > t c |t_k|>t_c ∣tk∣>tc,并且 β k \beta_k βk的符号与 H A H_A HA隐含的符号相同(符合预期),则拒绝 H 0 H_0 H0
- 根据P值判断:如果P值小于研究所要求的显著性水平,且 β k \beta_k βk的符号与 H A H_A HA隐含的符号相同(符合预期),则拒绝 H 0 H_0 H0
计量经济学分析中,大多数情况采用单侧检验
采用双侧检验的情况:估计值得符号没有明确得预期或者是否显著性于某个特定的值
永远牢记:不要把t检验得出的统计显著性等同于理论的有效性
在回归分析中,t检验不能检验相应变量的相对“重要性”,检验数字特征要用到统计检验,后面会提到
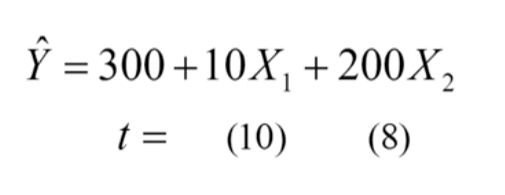
t检验的陷阱:随着样本容量的增大,t值会越来越大的原因在于:标准误会随着样本数量增加而减小,标准误越小t统计量就会越大
对于一个超大规模的样本而言,t检验没有任何意义,因为你几乎可以拒绝任何原假设
综上所述,t检验的局限性
- t检验不能检验理论有效性
- t检验不能检验“重要性”
- t检验不是针对总体的检验
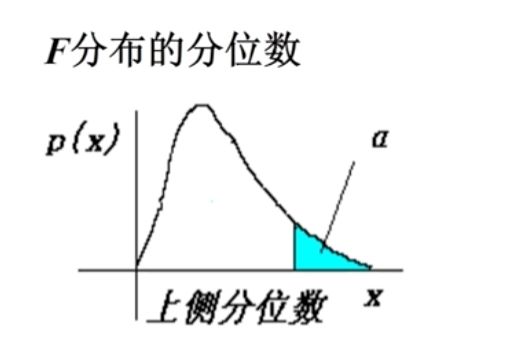
F检验
F = ( R S S R − R S S U R ) / J R S S U R / ( n − k ) F=\frac{(RSS_R-RSS_{UR})/J}{RSS_{UR}/(n-k)} F=RSSUR/(n−k)(RSSR−RSSUR)/J
其中J为约束条件个数,K为估计的参数个数(包括 β 0 \beta_0 β0)
对多个假设的联合检验或对线性约束的假设检验不能用t检验,只能用F检验
一种检验思路
- 将线性约束(原假设)代入线性回归方程,可得约束最小二乘估计量
- 约束最小二乘的拟合将劣于无约束最小二乘的拟合,即约束导致拟合的损失
- 约束最小二乘的RSS将大于无约束最小二乘的RSS,可据此构建统计量
检验规模报酬不变
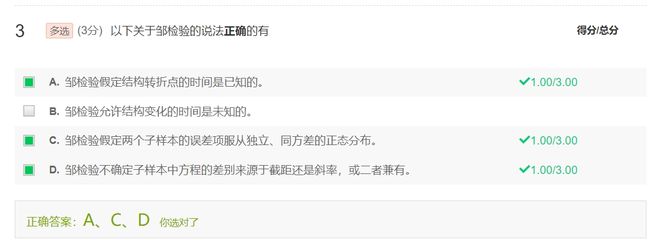
邹检验
结构变化:时间序列回归中,模型的参数在整个样本期间内可能发生变化
- 邹检验的假定:两个子时期回归的误差项是独立且具有同方差的正态分布变量
- 邹检验只告诉我们不同时期的回归方程是否有差别,并没有告诉我们差别来自截距,斜率还是二者兼有
- 邹检验假定我们知道结构转折点
正态性检验
采用JB检验(雅克-贝拉检验)
小结
- 通常,确定被解释变量后,应用回归分析采用六个步骤:
a. 查阅文献,建立理论模型
b. 确定模型:选择解释变量及函数形式
c. 对参数的符号做出假设
d. 搜集、检查和整理数据
e. 估计和评价方程
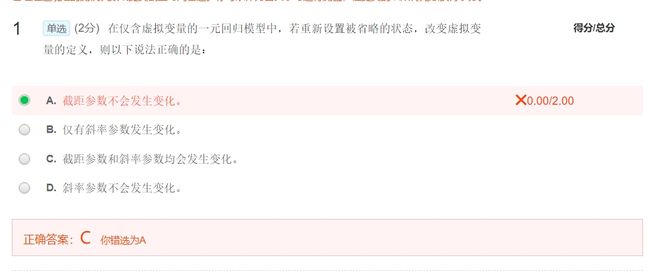
f. 报告结果 - 虚拟变量只能取值0或1,这取决与是否满足某些特定状态条件。虚拟变量的例子就是当为女性时X等于1,为男性时X等于0
例题
第四章 模型设定
正确的方程
- 正确的解释变量
- 正确的函数形式
- 正确的随机误差项
如何正确的选择解释变量
- 最重要的选择依据:(经济理论判断)
- 若理论上不明确,则可采用统计方法来判断
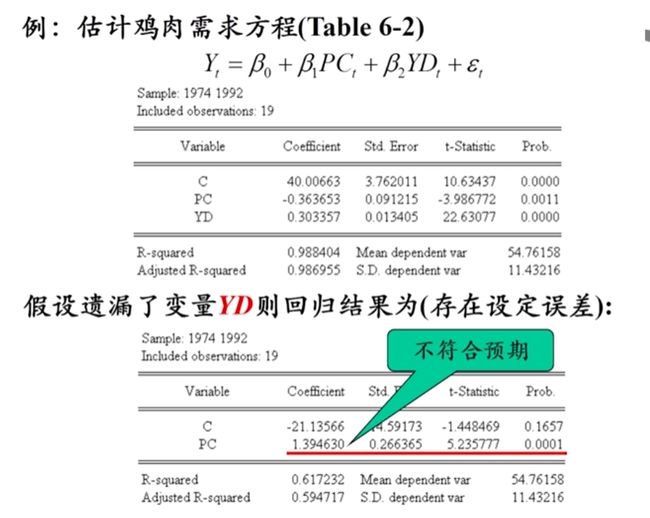
- 遗漏变量
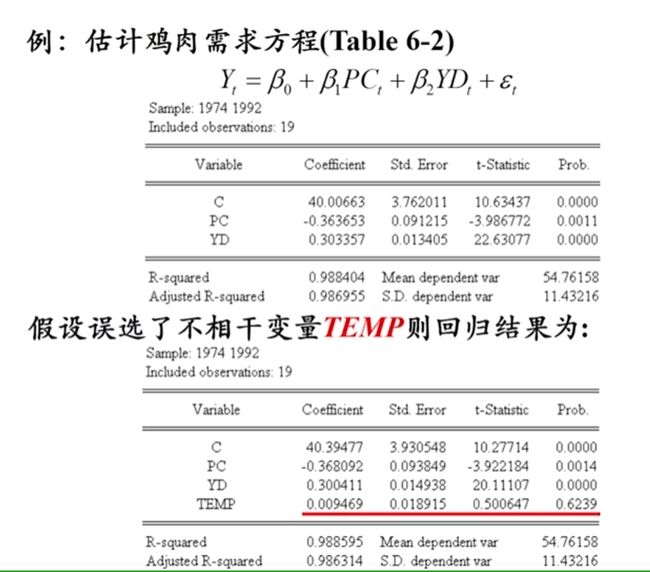
- 不相干变量
遗漏变量的后果
设定偏误:参数估计量有偏且非一致,方差变小
加入不相干变量的后果
参数估计量无偏但非有效(方差变大),t检验失效
模型选择准则
- 判定系数
R 2 = 1 − R S S T S S R^2=1-\frac{RSS}{TSS} R2=1−TSSRSS
R 2 ˉ = 1 − ∑ e i 2 / ( n − k ) ∑ y i 2 / ( n − 1 ) = 1 − ( 1 − R 2 ) n − 1 n − k \bar{R^2}=1-\frac{\sum e_i^2/(n-k)}{\sum y_i^2/(n-1)}=1-(1-R^2)\frac{n-1}{n-k} R2ˉ=1−∑yi2/(n−1)∑ei2/(n−k)=1−(1−R2)n−kn−1 - 赤池信息准则(AIC)和施瓦茨信息准则(SC)
A I C = 2 k n + l n R S S n AIC=\frac{2k}{n}+ln{\frac{RSS}{n}} AIC=n2k+lnnRSS 如果你加入一个新的解释变量那么AIC会增大 2 n \frac{2}{n} n2
S C = k n l n n + l n R S S n SC=\frac{k}{n}lnn+ln{\frac{RSS}{n}} SC=nklnn+lnnRSS 如果加入一个新的解释变量那么SC会增大 l n n n \frac{lnn}{n} nlnn
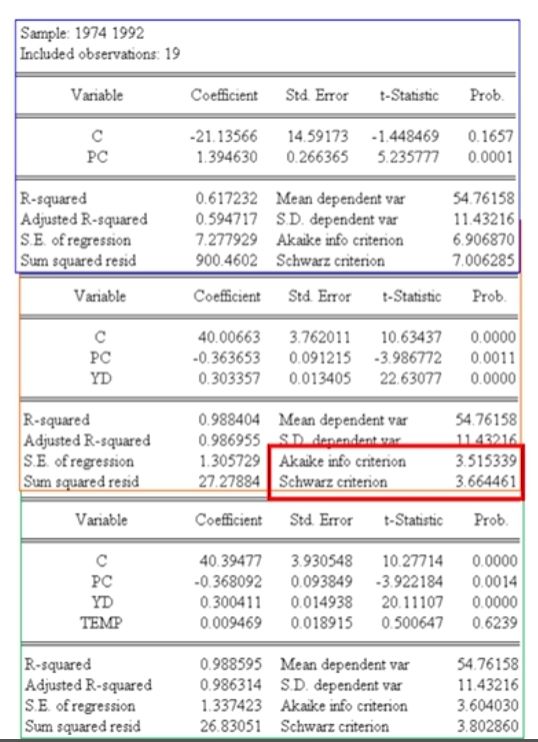
AIC和SC准则对增加解释变量加大了惩罚,其中SC的惩罚比AIC更严厉。相对而言,AIC和SC的值越低的模型越好。
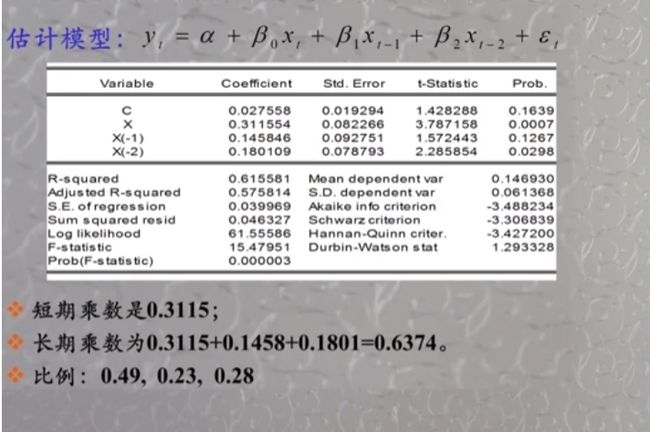
看下面的例子,可以发现中间的AIC和SC值是最小的,该模型也确实更好
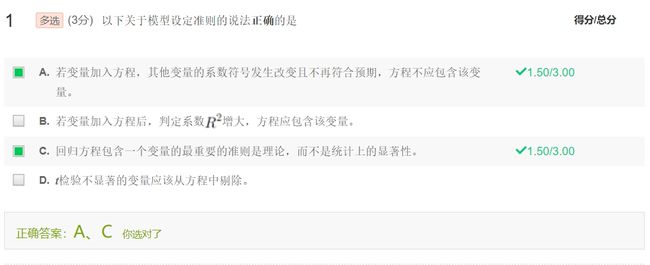
模型设定的四个重要准则
- 理论:变量在方程中的含义是不是模糊不清的,从理论上看是不是合理的?
- t检验:变量的待估参数在预期假设下是否显著?
不能简单地将一个t值不显著的变量从方程中排除,要结合理论与实际
- 调整的判定系数 R 2 ˉ \bar{R^2} R2ˉ或AIC和SC:在变量加入后,方程的整体拟合优度(自由度调整后)是否得到了改善
- 偏误:变量加入方程后,其他变量的参数值是否发生了显著性改变?
模型设定搜索
- 数据挖掘
- 适当的数据挖掘也许有助于揭示经济学理论尚未说明的经验规律
- 不适当的数据挖掘,比什么都不做更坏:如果你对数据严刑拷打,它就会屈打成招
- 敏感性分析:稳健性分析
- 几乎所有学术论文的必备步骤和分析内容
- 稳健的含义:某种结果对于各种模型设定,变量定义,数据子集都是显著的(或不显著的)
解释变量选择小结
- 由于遗漏变量在某种程度上都与已包含变量之间有相关性,因此,遗漏变量会导致方程中剩余变量的参数估计值产生偏误。
- 由遗漏变量所引起的偏误等于遗漏变量的参数乘以已包含变量和未包含变量的简单相关系数的函数。
- 方程中包含一个真正的不相关变量并不会因此偏误,但会增加已包含变量参数估计值的方差,因此会使t统计量和调整的判定系数 R 2 ˉ \bar{R^2} R2ˉ都降低。
- 方程中包含一个变量的四个有用准则:
a. 理论
b. t检验
c. 调整的判定系数 R 2 ˉ \bar{R^2} R2ˉ
d. 偏误 - 回归方程中包含一个变量的最重要的准则是理论,而不是统计上的显著性,否则存在产生错误或不可信结果的风险
错误函数形式的后果
- 影响解释变量的显著性
- 解释变量可能有非预期的符号
- 严重影响模型解释和变量预测
函数的选择形式
不含常数项的回归
Y i = β i X i + ϵ i Y_i=\beta_i X_i+\epsilon_i Yi=βiXi+ϵi
可以证明:
- 残差均值不一定为0
- 拟合优度的判定系数可能出现负值
除非有非常强的先验预期,否则还是采取含有常数项的模型为好;即使先验预期为无常数项模型,仍可使用含常数项的模型,再检验其常数项在统计上等于0即可
可线性化的非线性函数形式
- 指数函数
- 对数函数
- 反函数形式
- 多项式形式
如何选择函数形式
- 选择经济理论给出的特定函数形式
- 所选模型的参数应满足一定的先验预期
- 当多个模型能很好地拟合数据时,研究者往往选择调的判断系数较高或者AIC和SC较低的模型。然而,当被解释变量Y被替换时,这些指标不能比较
函数形式选择小结
- 即使理论上常数项可以等于零,也不能剔除常数项。另外,尽管常数项的估计值在理论上是显著的,也不能对常数项进行推理
- 函数形式的选择必须基于潜在的经济理论,也就是说要根据理论上的曲线形状去选择相应的函数形式。除非有特别要求需要选择其他形式,模型中变量的函数形式通常都是选用变量是线性的方程。
- 变量是非线性的函数形式包括双对数形式,半对数形式以及多项式形式。双对数形式特别适用于弹性是固定的模型中。半对数形式能用于哪些随着解释变量的增加,解释变量对于被解释变量的影响逐渐变小的模型中。多项式形式通常用于斜率符号会随着解释变量的不断变化而改变的模型中。
- 斜率虚拟变量是由一般解释变量和虚拟变量的成绩构成的。其中,这个一般解释变量于被解释变量之间的斜率会因为虚拟变量的设定状态是否被满足有所不同。
- 使用非线性函数形式存在一系列的潜在问题。特别地,如果解释变量Y的函数形式不同,则各个模型的调整的判定系数 R 2 ˉ \bar{R^2} R2ˉ不能进行比较;此外,如果选择了错误的函数形式对样本范围外进行预测,那么,预测结果的残差可能会非常大。
例题
第五章 多重共线性
多重共线性定义
回归模型中的一些或者全部解释变量之间存在一种完全或不完全的线性关系。
完全多重共线性:
λ 1 X 1 + λ 2 X 2 + . . . + λ k X k = 0 \lambda_1X_1+\lambda_2X_2+...+\lambda_kX_k =0 λ1X1+λ2X2+...+λkXk=0
不完全多重共线性:
λ 1 X 1 + λ 2 X 2 + . . . + λ k X k + v i = 0 \lambda_1X_1+\lambda_2X_2+...+\lambda_kX_k + v_i=0 λ1X1+λ2X2+...+λkXk+vi=0
只要不是完全多重共线性,用OLS仍可以得到参数的估计值及其标准误,并且仍是无偏,尽管无偏,但估计量的标准误非常大,即估计的精度很小。
多重共线性可能会导致估计量的标准误偏大,同时可能导致参数的估计值的符号与预期符号不符。
若总体中各解释变量X之间没有线性关系,样本中各解释变量X之间也可能存在线性关系。
多重共线性本质上是一种样本现象。
不完全多重共线性的特征
- 偏回归系数的t值会降低,倾向于统计上的不显著;
- 估计量(偏回归系数)对模型设定的变化非常敏感,估计系数可能出现非预期的符号或难以置信的数值;
- 虽然系数不显著,但总的拟合优度 R 2 R^2 R2却可能非常高
- 可能出现每个偏回归系数的t值都不显著,但回归方程的F值却很显著。
不完全多重共线性对预测的影响
- 如果回归分析的唯一目的是预测,并且如果不完全共线性的结构在样本和未来都保持一致,那么不完全多重共线性不是一个严重的问题
- 如果不完全共线性的结构在未来发生变化,则预测是冒险的
多重共线性的来源
- 经济变量之间具有共同变化的趋势
如经济繁荣时期,基本经济变量都趋于增长;衰退时期又同时趋于下降
- 模型中包含滞后变量
考察当期收入和前期收入对消费的影响,两期收入间有较强的线性相关性
- 横截面数据之间存在相关性
生产函数中资本投入与劳动力投入往往出现高度相关的情况,大企业二者都大,小企业都小
多重共线性的诊断
- 解释变量之间的相关系数 如果有多个变量,采用偏相关系数的方法
- 回归模型估计结果 R 2 R^2 R2F统计量显著,但是单个变量不显著,并且有些变量参数符号不符合预期 经验做法
- 方差膨胀因子(VIF)
多重共线性的补救措施
- 剔除支配变量
支配变量:与被解释变量高度相关,以致于完全掩盖了方程中其他解释变量的影响(如销售量与销售额)
- 增加样本容量
样本越大,估计越精准
- 剔除多余变量
潜在的理论假设作为剔除的主要依据
- 变换解释变量
- 一阶差分
- 两个变量相除
- 构造一个多重共线性的组合
- 主成分分析法
- 因子分析法
- 什么都不做
小结
- 完全多重共线性违背了一个解释变量不能是其他或多个解释变量的完全线性函数的古典假设。完全多重共线性会导致回归参数估计值的不确定性,并使得这些估计值具有巨大的标准差,从而使得普通最小二乘法不再适用
- 使用“多重共线性”一词时,通常指的是不完全多重共线性。不完全多重共线性指的是两个或多个解释变量之间存在较强的线性关系,以至于能够显著地影响方程中解释变量的参数估计。多重共线性问题既是一种样本现象,同时也是一种理论现象。不同的样本可能存在不同程度的多重共线性。
- 严重的多重共线性产生的主要结果是增大了回归参数估计量的方差,同时使得这些参数估计值的t统计量变小,扩大了置信区间。多重共线性不会导致参数估计值有偏,它对于回归方程的整体显著性或者任何一个不是多重共线性的解释变量的参数估计值都几乎没有多少影响。
- 由于在不同数据集中多重共线性的程度会有显著的不同,所以,在诊断多重共线性时需要注意的问题就是:在一个特定的样本当中,多重共线性究竟有多严重。
- 用来诊断严重多重共线性的两种有用的方法是:
a. 解释变量之间的简单相关系数是否很高? 一般来看,相关系数的绝对值如果大于0.80,则认为很高。
b. 方差膨胀因子是否很高?一般来看当 V I F ( β i ^ ) > 5 VIF(\hat{\beta_i}) > 5 VIF(βi^)>5,则存在严重的多重共线性。如果两个答案中任意一个是“是”,则多重共线性确实存在,但是当答案同时为“否”时,也可能存在多重共线性问题。
- 针对多重共线性有如下三种最为常用的补救措施:
a. 什么都不做(这样可以避免方程设定偏误)
b. 去除多余的变量
c. 增大样本容量 - 对于多重共线性的问题,什么都不做往往是最好的补救措施。假如多重共线性没有使t统计量减少到不显著的程度,那么就不需要对多重共线性采取任何补救措施。即使t统计量不显著,针对多重共线性所采取的补救措施也必须谨慎,因为补救所带来的估计成本,可能比从方程中消除多重共线性所获得潜在收益还要大。
例题
第六章 序列相关性
序列相关性的形式
- 一阶序列相关
干扰项只与其滞后一期值相关 ε t = f ( ε t − 1 ) \varepsilon_t=f(\varepsilon_{t-1}) εt=f(εt−1)
- 高阶序列相关
干扰项与其滞后多期值相关 ε t = f ( ε t − 1 , ε t − 2 , . . . ) \varepsilon_t=f(\varepsilon_{t-1},\varepsilon_{t-2},...) εt=f(εt−1,εt−2,...)
序列相关通常假定为线性序列相关,最常见的形式为一阶序列相关
ε t = ρ ε t − 1 + u t \varepsilon_t=\rho\varepsilon_{t-1}+u_t εt=ρεt−1+ut
其中, ρ \rho ρ为一阶自相关系数,且 ∣ ρ ∣ < 1 |\rho|<1 ∣ρ∣<1; u t u_t ut为白噪声序列,满足 E ( u t ) = 0 , V a r ( u t ) = σ u 2 , C o v ( u t , u t + s ) = 0 , s ≠ 0 E(u_t)=0,Var(u_t)= \sigma_u^2,Cov(u_t,u_t+s)=0,s \ne 0 E(ut)=0,Var(ut)=σu2,Cov(ut,ut+s)=0,s=0
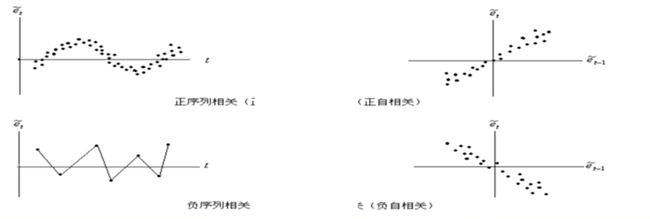
根据自相关系数 ρ \rho ρ,序列相关可分类如下
- $\rho > 0 \to $ 正序列相关
- $\rho < 0 \to $ 负序列相关
- $\rho = 0 \to $ 无序列相关
序列相关类型
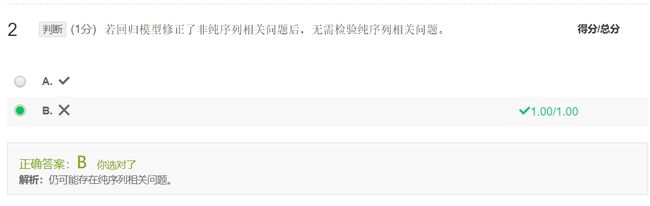
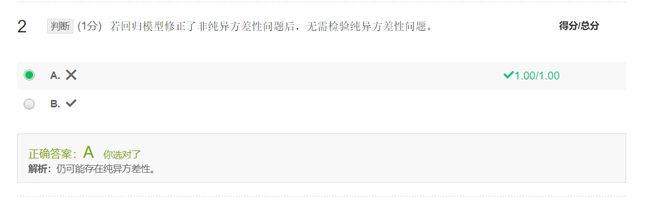
- 非纯序列相关
- 由设定偏误导致,如遗漏变量、不正确的函数形式等
- 纯序列相关
- 时间序列数据:对同一总体的连续的观测很可能表现出某种系统的相关性,特别是连续观测时间间隔很短,如一周,一天,甚至同一天多次观测
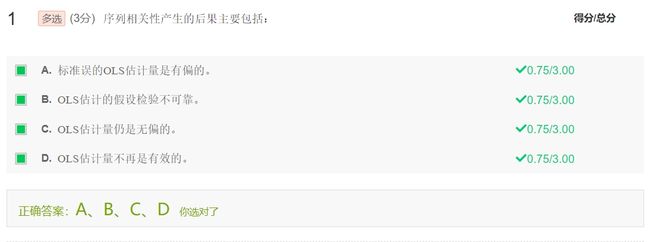
序列相关的后果
在纯序列相关性的情形下
- OLS估计量仍是无偏的
- OLS估计的假设检验不可靠
- OLS估计量不再是有效的(即最小方差估计量)
- 标准误的OLS估计是有偏的,且偏差通常是负的,意味着OLS通常会高估参数的t值,导致原本不显著的变量可能变得显著
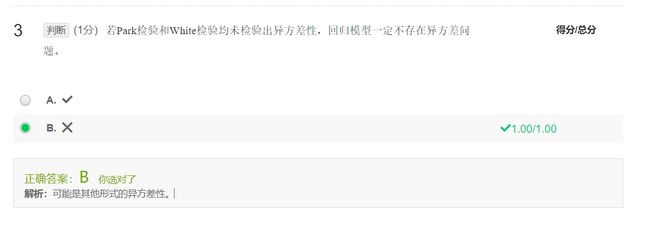
序列相关的检验
检验思路:检验序列相关,也就是检验随机误差项之间的相关性及“形式”
因随机误差项的样本对应物是OLS的残差,因此所有的检验都基于残差
常用检验方法
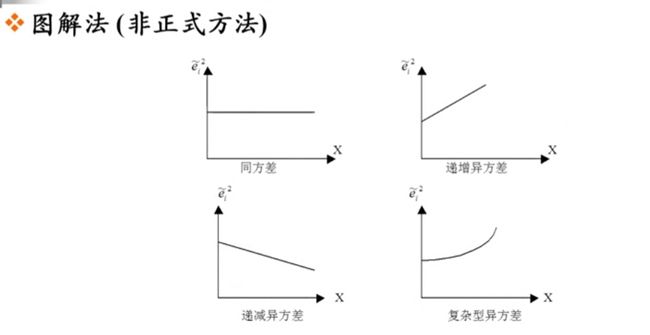
- 图解法
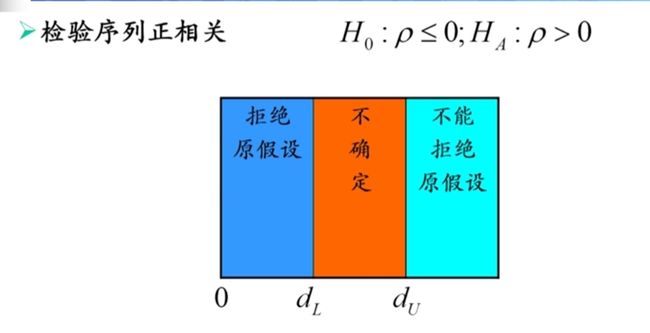
- 杜宾——沃森(DW)检验
- BG检验
图解法
将残差对时间描点,以发现残差在时间上的特定关联
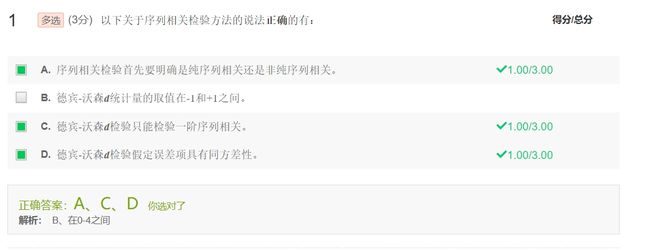
杜宾——沃森(DW)检验
利用方程的残差构成统计量,推断误差项是否存在一阶序列相关
基本假定
-
回归模型包含截距项
-
序列相关是一阶序列相关
-
回归模型不能把滞后被解释变量作为解释变量
-
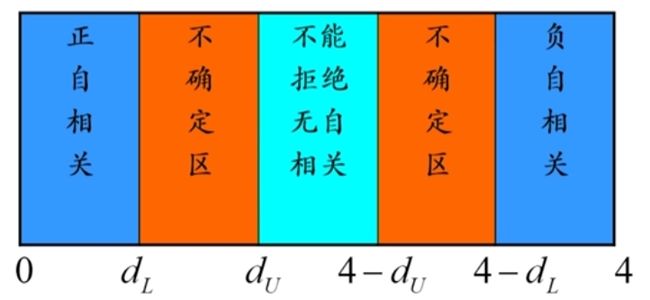
d检验值为0,意味着序列存在完全正相关
-
d值为2意味着不存在序列相关性
-
d值为4意味着序列存在完全负相关。
-
0 < d < 2 → 0 < ρ < 1 0 < d < 2 \to 0 < \rho < 1 0<d<2→0<ρ<1
-
2 < d < 4 → − 1 < ρ < 0 2 < d < 4 \to -1 < \rho < 0 2<d<4→−1<ρ<0
d统计量的检验
- 由于d统计量依赖于残差,而残差又依赖于X,故无法推导出d统计量的准确分布
- D-W根据样本容量n和待估参数k,在给定显著性水平下,给出了d统计量上,下两个临界值 d U 和 d L d_U和d_L dU和dL
DW检验的缺陷
- 当d统计量落在两个不确定区域时,无法判断是否存在序列相关
- 当滞后因变量作为解释变量,检验无效
- 只能检验一阶序列相关,不适用于高阶序列相关
- 若误差项不是IID正态分布,d检验也不可靠
BG检验
这里 ε t \varepsilon_t εt没有常数项是因为其期望值为0
序列相关的补救措施
非纯序列相关
实际中,有时只要迭代两次,就可得到较满意的结果。两次迭代过程也被称为**科克伦-奥科特两步法 **
几点说明
- GLS的DW检验值和调整的 R 2 R^2 R2不能与OLS进行比较
- GLS的估计值通常与OLS的估计值不同
- 在小样本中,因相关系数的估计可能有偏,GLS估计的系数可能也是有偏的
-
AR方法
-
Newey——West方法
- 只修正标准误而不会改变系数的估计值
- 在大样本估计中,效果更好
- 绝大多数学术论文采用此种方法
小结
- 序列相关,也叫自相关,违背了古典假设四(即误差项的值彼此不相关)。通常,计量经济学家更多关注的是1阶序列自相关,即误差项当前值是前1期值和序列不相关的误差项u的函数:
ε t = ρ ε t − 4 + u t , − 1 < ρ < 1 \varepsilon_t=\rho\varepsilon_{t-4}+u_t, -1<\rho<1 εt=ρεt−4+ut,−1<ρ<1 - 纯序列相关是正确设定的回归方程中误差项的相关函数。非纯序列相关是由遗漏了变量或选择了不正确的函数形式等错误设定引起的,可以为正相关( 0 < ρ < 1 0<\rho<1 0<ρ<1),也可以为负相关( − 1 < ρ < 0 -1<\rho<0 −1<ρ<0)。在经济和商业环境下,纯序列相关几乎都是正相关。
- 序列相关性的主要后果是采用普通最小二乘法估计的SE ( β ^ ) (\hat{\beta}) (β^)是有偏的,导致假设检验不可靠。纯序列相关不会造成参数 β \beta β的有偏估计。
- 诊断1阶序列相关性最常用得到方法是杜宾——沃森d检验。它用回归估计的残差检验误差项是否存在序列相关性。d检验值为0,意味着序列存在完全正相关,d值为2意味着不存在序列相关性,d值为4意味着序列存在完全负相关。
- 消除方程序列相关性的第1步时检查可能存在的设定错误,只有当非纯序列相关存在的可能性很小时,才能考虑修正纯序列相关性。
- 广义最小二乘法(GLS)是通过变换方程以消除纯1阶序列相关的方法。运用广义最小二乘法时需要 ρ \rho ρ的估计值。
- Newey-West标准差时另一种修正序列相关性的方法。这种方法在考察序列相关性时,在不改变估计量值 β ^ \hat{\beta} β^的情况下,调整普通最小二乘估计的标准差SE ( β ^ ) (\hat{\beta}) (β^)
例题
第七章 异方差性
异方差类型
非纯异方差
- 由设定偏误导致,如遗漏变量
- 函数设定形式不当一般不会导致非纯异方差
纯异方差
- 横截面数据:被解释变量取值差异较大
- 时间序列数据:学习效应,数据采集技术的变化
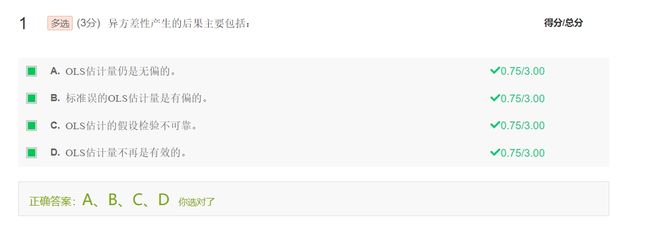
纯异方差的后果
- OLS估计量仍然是无偏的
- OLS估计量不再是有效的(即最小方差估计量)
- 标准误的OLS估计量是有偏的,且偏差通常是负的,意味着OLS通常会高估参数的t值,导致原本不显著的变量可能变得显著
若存在异方差,OSL估计的假设检验不可靠
异方差的检验
检验思路:检验异方差,也就是检验随机误差项的方差与比例因子Z或解释变量X之间的相关性及其“形式”
因随机误差项方差的样本对应物是OLS的残差平方,因此所有的检验方法都基于残差平方
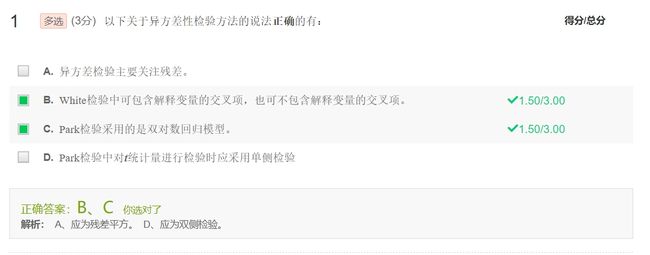
*white(怀特)检验
基本思想:异方差来源于解释变量及其高次方
Y i = β 0 + β 1 X 1 i + β 2 X 2 i + ε i Y_i=\beta_0+\beta_1X_{1i}+\beta_2X_{2i}+\varepsilon_i Yi=β0+β1X1i+β2X2i+εi
步骤1:假设同方差,OLS估计获得残差
步骤2:做辅助回归并得到拟合优度 R 2 R^2 R2
![]()
步骤4:若计算的 n R 2 nR^2 nR2超过选定显著性水平的临界值,则拒绝同方差假设。
有一个经验判断,如果white检验中不包含交叉项,则主要针对异方差性的检验,如果包含交叉项的话,这个检验就是针对模型设定偏误和异方差性的联合检验
异方差的补救措施
- 非纯异方差
- 正确的模型设定
- 纯异方差
- 广义最小二乘法:加权最小二乘(WLS)
- 使用WLS的前提是知道比例因子Z及其与误差项方差之间的关系,即权重向量P
- 修正异方差的标准误:White方法
- 只修正标准误而不会改变系数的估计值
- 在大样本估计中,效果更好
- 绝大多数学术论文采用此种方法
- 重新定义新变量
- 将某些变量,特别是被解释变量取对数
- 根据经济理论,对某些变量进行“规模调整”
- 广义最小二乘法:加权最小二乘(WLS)
小结
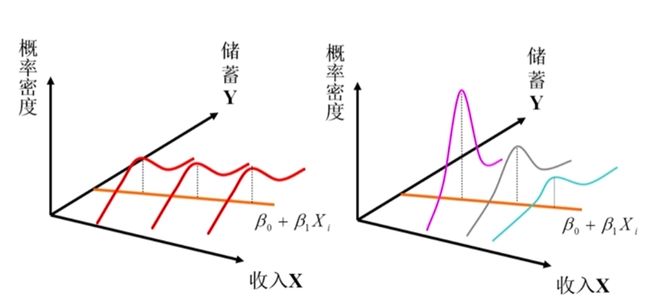
- 古典假定5要求误差项应服从相同方差的分布,而异方差性正是对此假定的违背。同方差的误差项的观测值的分布是,对于所有观测值而言都具有相同的方差;异方差性的误差项观测值的分布是,对于不同观测值而言,方差不完全相同。界面是数据模型中,最常产生异方差性。
- 异方差性误差项的方差不等于常数 σ 2 \sigma^2 σ2,而等于 σ i 2 \sigma_i^2 σi2(其中下标表明方差随观测值的不同而变化)。异方差性有许多种,但是最常用的异方差性模型是将方差看成某个其他变量(比例因子Z)的函数
V A R ( ε i ) = σ 2 Z i 2 VAR(\varepsilon_i)=\sigma^2Z_i^2 VAR(εi)=σ2Zi2
比例因子通常是跟被解释变量的规模或者精确度相关联的一个变量 - 纯异方差性是指异方差性是由误差项的一个函数所表示的,而该误差项是设定正确的方程回归得到的。纯异方差性是由方程设定偏误(比如遗漏变量)导致的。
- 异方差性的主要后果是:最小二乘法的SE ( β ^ ) (\hat{\beta}) (β^)有偏,从而导致假设检验的结果不可信。纯异方差性并不导致 β \beta β本身的偏误。
- 检验异方差性的主要方法是BP检验和White检验,他们都是通过分析原方程的残差平方可以被辅助方程解释的程度来检验异方差性的。
- 修正异方差性的第一步是检查异方差性是否因为遗漏变量而引起的非纯异方差性。如果方程设定正确,那么,就可以考虑采用HC标准差,重新定义变量等措施对异方差性进行补救。
例题
第八章 虚拟变量模型
经济变量
- 可以度量的变量:商品需求量,价格,收入,产量等
- 无法定量度量;职业,性别,战争,自然灾害等
虚拟变量:定性变量

解答:因为如果加入东部,那么三个虚拟变量相加等于1,就会存在多重共线性
虚拟变量的设置原则
- 每一定性变量所需的虚拟变量个数要比该定性变量的类别少1,即如果有m个定性变量,只能在模型中引入m-1个虚拟变量
- 在同一方程中,可以引入多个虚拟变量来考察多种定性因素的影响
虚拟变量的引入
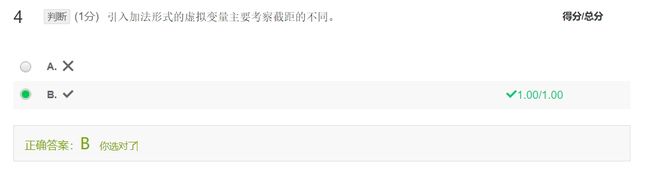
- 加法形式:考察截距的不同
Y i = β 0 + β 1 X i + β 2 D i + μ i Y_i=\beta_0+\beta_1X_i+\beta_2D_i+\mu_i Yi=β0+β1Xi+β2Di+μi - 乘法形式:考察斜率的不同
C t = β 0 + β 1 X t + β 2 D t X t + μ t C_t=\beta_0+\beta_1X_t+\beta_2D_tX_t+\mu_t Ct=β0+β1Xt+β2DtXt+μt - 混合形式: 截距和斜率同时发生变化
Y i = β 0 + β 1 X i + β 3 D i + β 4 ( D i X i ) + μ i Y_i=\beta_0+\beta_1X_i+\beta_3D_i+\beta_4(D_iX_i)+\mu_i Yi=β0+β1Xi+β3Di+β4(DiXi)+μi
计量经济学中的实验方法
随机分配实验
- 处理组:参与实验人员
- 对照组或控制组:未参与实验人员
自然实验 - 观测值自然产生,由外生事件引起
- 自然时间,政策变动
例题
第九章 虚拟应变量模型
虚拟应变量的概念
- 虚拟变量既可以作为解释变量,又可以作为被解释变量(应变量)
- 虚拟应变量模型又称为概率模型,离散选择模型
- 二元选择模型
- 多元选择模型
LPM模型存在的问题:
- D i ^ \hat{D_i} Di^的取值可能不在0和1之间
- 调整的判定系数 R 2 ˉ \bar{R^2} R2ˉ不能准确度量方程的拟合优度
- 随机干扰项不服从正态分布,且存在异方差
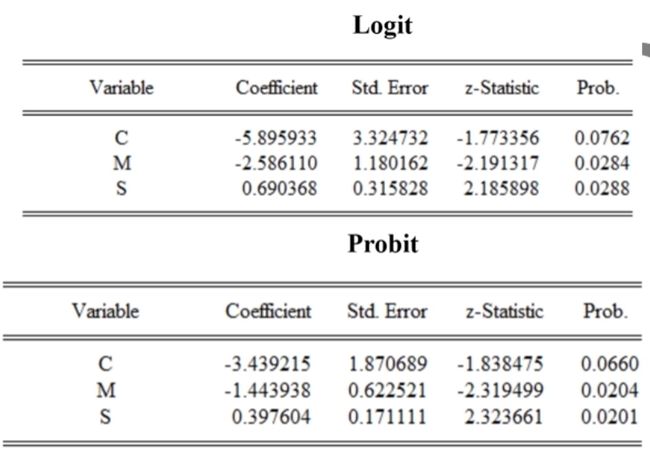
采用极大似然估计法来估计Logit模型和Probit模型
因为这两种方法的分布函数不同,会得到不同的结果,这两组系数不能直接比较,但是二者系数存在一定的关系
标准正态分布的方差为1,而标准逻辑分布的方差为 π 2 / 3 \pi^2/3 π2/3,因此将Probit系数乘以 π / 3 \pi/ \sqrt 3 π/3(约1.81),就会近似得到Logit系数(约为0.55)
其它虚拟应变量模型
- 多元Logit模型
- 被解释变量存在多种离散且无序的选择
- 如择业的选择,交通工具的选择
- 采用极大似然估计
- 序次Logit模型
- 被解释变量存在多种离散且有序的选择
- 如债券的评级,舆论调查结果
- 采用极大似然估计
补充
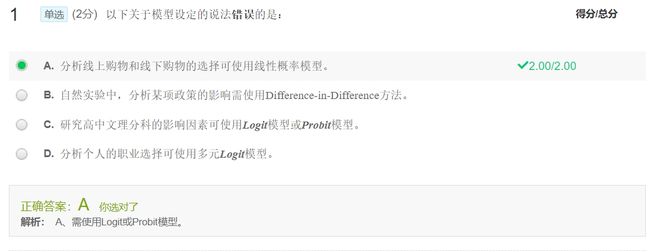
- 当被解释变量是虚拟变量时,不能采用线性概率模型(OLS估计方法)
- Logit和Probit模型可用于估计被解释变量是二分应变量(二元选择)的问题
- 在解释变量是多元选择问题中,可以采用多元Logit模型或次序Logit模型
小结
- 线性概率模型是用来解释虚拟变量 ( D i ) (D_i) (Di)的参数线性方程, D i ^ \hat{D_i} Di^是 D i D_i Di等于1的概率
- 采用普通最小二乘法估计线性概率模型会出现三个主要问题:
a. 调整的判定系数 R 2 ˉ \bar{R^2} R2ˉ不能准确度量模型的整体拟合优度
b. D i ^ \hat{D_i} Di^的期望值不是以0和1为界
c. 误差项既不是同方差的,也不是正态分布的 - 在度量虚拟被解释变量的整体拟合优度时,可以采用样本观测值被模型正确解释的百分比 R P 2 ˉ \bar{R_P^2} RP2ˉ来代替判定系数 R 2 ˉ \bar{R^2} R2ˉ
- 二元logit模型是一种采用累积logistic函数的变形来回避线性概率模型无界性问题的虚拟被解释变量模型估计方法。模型形式为:
L : P r ( D i = 1 ) = l n ( P i [ 1 − P i ] ) = β 0 + β 1 X 1 i + β 2 X 2 i L:Pr(D_i=1)=ln(\frac{P_i}{[1-P_i]})=\beta_0+\beta_1X_{1i}+\beta_2X_{2i} L:Pr(Di=1)=ln([1−Pi]Pi)=β0+β1X1i+β2X2i - 二元logit模型最好在大样本条件下采用最大似然法估计,logit模型的斜率参数表示:在其他解释变量保持不变的情况下,特定解释变量每增加1单位对给定选择的概率的对数的影响。
- 二元probit模型是一种利用累计正态分布函数的变形来规避线性概率模型无界性问题的虚拟被解释变量模型估计方法。二元probit模型与二元logit模型的特征非常相似
例题
第十章 预测
预测共性
- 被预测的变量的都是未知的(样本外)
- 仅能预测变量的期望值(随机性)
预测是对被解释样本外的观测值的期望值的估计
计量模型的预测步骤
- 搜集相关数据,建立回归模型
- 估计模型
- 将预测期解释变量的值代入模型,进行预测
- 评价预测效果
时间序列模型预测
时间序列分析:“让数据自己说话”
- 传统计量模型以理论为基础,而社会经济现象往往受多种因素影响且这些因素存在错综复杂的联系,使得根据理论建模较为困难
- 依据经济变量自身的历史资料,采用一定的统计方法,建立起能反映变量自身规律性的动态模型,以此对经济变量进行分析和预测
平稳性检验:单位根检验
- 存在单位根的时间序列的一阶差分为平稳序列
- 常用方法为DF检验,ADF检验
- 检验的原假设为:时间序列存在单位根
预测方法
- 动态预测:从预测样本的第一期开始计算多步预测
- 静态预测:利用滞后项被解释变量的实际值计算1步预测
静态预测效果更好
复杂模型的预测能力不一定强于简单模型
预测仅仅是计量经济学的用途之一,不要过分相信计量经济学模型的预测能力!
小结
- 预测就是根据样本范围外的观测值来估计被解释变量的期望值。基本方法是将想要预测的变量作为被解释变量估计一个方程,然后将各个解释变量(需预测的观察结果)的值带入方程中计算出预测值。
- 一个预测方程在样本范围内拟合得很好,并不能保证也可以对样本范围外得观测值进行准确的预测。
- 确切地知道每一个解释变量的值的预测叫做无条件预测,但如果有一个或多个解释变量的值要通过预测得到,那么这种预测叫做条件预测。条件预测所得到的Y的预测值是无偏的(只要X的预测值是无偏的),但是一定会使误差方差变大。
- 如果方程的参数是用广义最小二乘法估计得出的(为了修正纯1阶序列相关),那么预测方程为:
Y T + 1 ^ = ρ ^ Y T + β 0 ^ ( 1 − ρ ^ ) + β 1 ^ ( X T + 1 ^ − ρ ^ X T ) \hat{Y_{T+1}}=\hat{\rho}Y_T+\hat{\beta_0}(1-\hat{\rho})+\hat{\beta_1}({\hat{X_{T+1}}-\hat{\rho}X_T}) YT+1^=ρ^YT+β0^(1−ρ^)+β1^(XT+1^−ρ^XT)
式中, ρ \rho ρ代表自相关系数 - 如果同时计算出置信区间,预测结果将会更加有意义。置信区间是指被解释变量的真实值落入该区间的次数为某固定百分比(置信水平)的某个区间。计算如下:
Y T + 1 ^ ± S F t c \hat{Y_{T+1}}\pm S_Ft_c YT+1^±SFtc
式中, S F S_F SF为预测的估计标准差, t c t_c tc为某置信水平下双侧检验的t的临界值 - ARIMA是一种高度精炼的曲线拟合方法,能用被解释变量(仅仅是被解释变量)的过去值和现在值来精确地预测该变量短期内的值,首先通过d阶差使序列变平稳,差分后的变量其均值和方差固定不变的。ARIMA(p,d,q)表示该模型是由p阶自回归过程(含有 θ 1 Y t − 1 \theta_1 Y_{t-1} θ1Yt−1)和q阶的平均移动过程(含有 ϕ 1 ε t − 1 \phi_1\varepsilon_{t-1} ϕ1εt−1)来表示d阶差分的被解释变量
例题
第十一章 时间序列模型
有限滞后模型(FDL)模型的估计
Y t = α 0 + β 0 X t + β 1 X t − 1 + . . . + β p X t − q + ε t Y_t= \alpha_0+\beta_0X_t+\beta_1X_{t-1}+...+\beta_{p}X_{t-q}+\varepsilon_{t} Yt=α0+β0Xt+β1Xt−1+...+βpXt−q+εt
存在的问题
- X的各期滞后项之间可能存在严重的多重共线性
- 参数估计值未必会符合经济理论具有平滑递减的特征
FDL模型估计的假设
- 参数是线性的
- 解释变量和误差项不存在完全共线性
- 零条件均值 (严格外生)
E ( ε t ∣ X ) = 0 E(\varepsilon_{t}|X)=0 E(εt∣X)=0
- 同方差性
- 无序列相关
- 正态性
FDL模型的特点
考伊克模型的特点
- 以滞后被解释变量代替了大量被解释变量的滞后项,节省了自由度
- 滞后被解释变量与解释变量的相关度较低,缓解了多重共线性
考伊克模型的问题 - 随机干扰项存在序列相关性
- 滞后被解释变量与随机干扰项不独立
该问题属于内生性问题,导致OLS估计量有偏
-
外生解释变量和内生解释变量
- 解释变量X与误差项 ε \varepsilon ε不相关,则称x为外生解释变量
- 解释变量X与误差项 ε \varepsilon ε相关,则称x为内生解释变量
-
解决内生性问题
- 在回归模型中增加遗漏变量进行控制
- 工具变量(IV检验),代理变量
简单的回归模型: y = β 0 + β 1 x + ε y=\beta_0+\beta_1x+\varepsilon y=β0+β1x+ε
C o v ( x , ε ) ≠ 0 o r E ( ε ∣ x ) ≠ 0 Cov(x,\varepsilon) \ne 0 or E(\varepsilon|x) \ne 0 Cov(x,ε)=0orE(ε∣x)=0
为了得到参数的一致估计,需要额外的信息。假设有一个可观测变量z,它满足两个条件:
- z和 ε \varepsilon ε不相关,即 C o v ( z , ε ) = 0 Cov(z,\varepsilon)=0 Cov(z,ε)=0
- z和x相关,即 C o v ( z , ε ) ≠ 0 Cov(z, \varepsilon) \ne 0 Cov(z,ε)=0
则称z是x的工具变量。
普通最小二乘估计是工具二乘估计(IV检验)的特殊形式
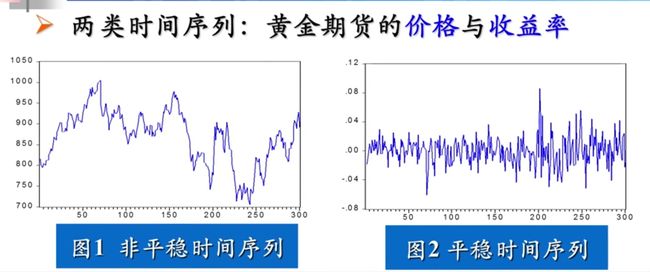
两组非平稳时间序列进行回归,会产生虚假的回归现象
小结
- 分布滞后项反应Y的当期值是X的当期值和过去值的函数,于是,将X的影响分布于滞后的若干期中。无约束分布滞后模型(特设分布滞后模型)的普通最小二乘估计会产生多重共线性问题,自由度问题和参数随时间的非连续变化问题。
- 动态模型通过假设滞后解释变量的参数随滞后项的加长而呈集合呈几何级数衰减回避了分布滞后模型面临的问题。给定这一假设,动态模型可以表述为:
Y t = α 0 + β 0 X t + λ Y t − 1 + u t Y_t=\alpha_0+\beta_0 X_t+\lambda Y_{t-1}+u_t Yt=α0+β0Xt+λYt−1+ut
式中, Y t − 1 Y_{t-1} Yt−1代表滞后被解释变量且 0 < λ < 1 0<\lambda<1 0<λ<1. - 在小样本条件下,动态模型的普通最小二乘估计存在偏误且假设检验不可靠。即使在大样本条件下,如果误差项存在序列相关性,普通最小二乘法在估计动态模型参数时仍会产生偏误。
- 在动态模型中,杜宾-沃森d检验有时不能检验出序列相关性,因为d偏向于2。另一种最常用的检测方法是拉格朗日乘数检验。
- Granger因果关系,也称前定关系,描述的是这样一种情形,即若某时间序列变量变动,另一个时间序列变量会发生一致的可预测的变化。即便一个变量前定(Greanger导致)另外一个变量,也不能认为第一变量的变动引起了另一个变量的变动。
- 非平稳序列是随时间发生显著变化(例如,均值和方差)的序列。如果被解释变量和至少一个解释变量是非平稳的,回归结果可能产生谬误相关,使得调整的判定系数 R 2 ˉ \bar{R^2} R2ˉ和非平稳解释变量的t统计量偏大。
- DF检验可以检验出非平稳性,如果变量是非平稳的(存在单位根),那么,就应该采用DF检验检验方程残差的平稳性,进而检验方差的协整性。如果变量存在单位根但并不协整,那么,把模型的函数形式转换为1阶差分,再估计方程。如果变量存在单位根并且是协整的,那么,以变量的原始形式估计方程。
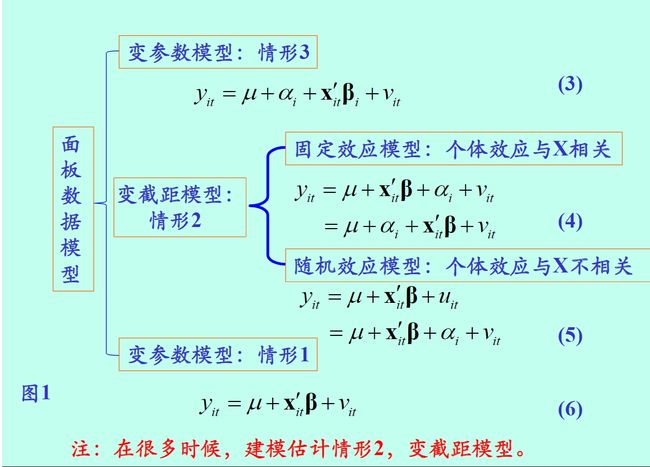
第十二章 面板数据模型
小结
- 随机分配实验被认为是证明一个实验(处理)因素与出现的结果间存在因果关系的黄金准则。随机选择的处理组暴露在实验(处理)下,对照组不受实验因素作用。我们检验组的结果是否有显著性差异。不幸的是,这种实验在经济学的许多领域都不可行。
- 如果一个自然发生的时间(如政策的改变)能够被看作模仿了一个随机分配实验过程,则该自然实验能够为经济学中的因果关系提供证据。如果该事件让处理组结果的均值比对照组的均值发生了更显著的变化,则我们有证据表明实验(处理)是使结果发生改变的原因。
- 涉及自然实验数据的方程可以用差异中的差分模型来估计,该模型比较了处理组和对照组结果改变量之间的差异。
- 面板数据(也称纵向数据)通过在两个或两个以上时间段采集的相同截面样本的相同变量的观测值的方法,结合了时间序列数据和截面数据。面板数据常常是由多年的大规模调查项目得来的,为计量经济学分析提供了丰富的数据资源。
- 涉及面板数据的方程可以用固定效应模型或者更先进的随机效应模型进行估计。