初级stata
b站教学视频
导入数据
use
画散点图
scatter 纵坐标变量 横坐标变量
scatter y x1 x2 …
回归分析
reg y x1 x2 x3 …
假设检验
正态分布
- 正态分布检验指令 sktset + 变量
Obs 样本值 Pr(skewness)是对偏度的正态分布检测值 Pr(kurtosis)是对其峰度的正态分布检验,chi(2)是对总体的正态分布检验,我们主要观看的是P值(Prob)如果P值大于0.05我们就认为其符合正态分布,否则不符合
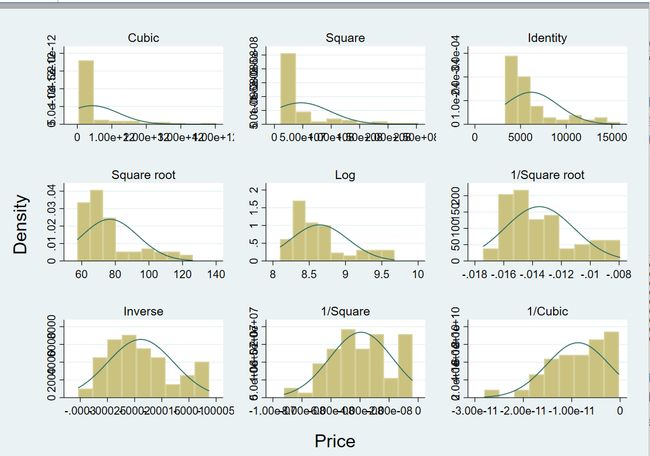
- 寻找变量正态化的方法 ladder+变量
Formula对数据的处理方法,主要看p值如果P值大于0.05我们就认为其符合正态分布,否则不符合
- 画出变量进行正态话处理后的图像 gladder+变量
t检验
- 单一样本T检验 ttest + 变量名 = 数值
通过单一样本T检验,我们可以实现样本均值与总体均值的比较。也就是说,是用来比较一组数据的平均值和一个数值有无差异
Mean是平均值,std.err为标准误,std.dev是标准差 95% conf.interval是95%水平的置信区间范围 自由度为观测样本数-1 t为t值 主要看P值如果小于0.05那么这组数据的平均值与给定的数据平均值有显著性差异,如果大于0.05那么则无显著性差异
- 单一样本T检验修改置信水平 ttest + 变量名 = 数值,level(99)
数据指标与上图一致,只是置信水平发生变化
- 独立样本T检验修改置信区间值 ttest 变量名=变量名,unpaired
通过独立样本T检验,我们可以实现两个独立样本的均值检验
其他表项与上述表项类似,主要看P值如果小于0.05那么两组数据有显著性差异,如果大于0.05那么则无显著性差异
- 独立样本T检验修改置信区间值 ttest 变量名=变量名,unpaired level(数值)
-
独立样本T检验两样本方差不同 ttest 变量名=变量名,unpaired unequal
-
配对样本T检验 ttest 变量名=变量名
通过配对样本T检验,我们可以实现对成对数据样本均值的比较,其与独立样本T检验的区别是:两个样本来自同一总体,而且数据的顺序不能调换。
主要看P值分析与上面一致
F检验
F检验又叫方差齐性检验。从两研究总体中随机抽取样本,要对这两个>样本进行比较的时候,首先要判断两总体方差是否相同,即方差齐性。若两总体方差相等,则直接用t检验,若不等,可采用t’检验或变量变换或秩和检验等方法。
从两研究总体中随机抽取样本,要对这两个样本进行比较的时候,首先要判断两总体方差是否相同,即方差齐性。若两总体方差相等,则直接用t检验,若不等,可采用t’检验或变量变换或秩和检验等方法。其中要判断两总体方差是否相等,就可以用F检验。
reg y x1 x2 x3 x4
test x1 x2 x4
test x2=0.3
注意除了y其他都能用test检验
邹检验
例题
建立鸡肉消费量Y对鸡肉价格PC、人均可支配收入YD的回归模型,采用1974-2002的数据估计参数(变量YEAR),检验1993年是否存在结构变化(邹检验),请写出相应的Stata的程序或命令(数据use CHICK6.dta)。
方法1
use CHICK6.dta
reg Y PC YD
scalar ssr = e(rss)
reg Y PC YD if year < 1993
scalar srr1 = e(rss)
reg Y PC YD if year >= 1993
scalar srr2 = e(rss)
gene f = ((ssr - ssr1 - ssr2) / 3) / (srr1 + srr2) / (29 - 6)
方法2
use CHICK6.dta
reg Y PC YD
estat sbknown,break(1993)
循环结构举例
参考博客
scaler j = 1
while j <= num{
matrix pvalue[j, 1] = 2*(1-t(rowsof(x)-colsof(X), abs(tvalue[j, 1])))
scalar j = j + 1 // 更新时也用scalar
}
正态性JB检验: jb6 X
需要提前安装 ssc install jb6
- 输出的第二个数大于0.05则可认为数据符合正态分布
多重共线性检验之VIF判断
estat vif
先回归再检测,如果vif大于5认为存在严重的多重共线性
序列相关性
序列相关性检验
先回归再检验
-
DW检验:estat dwatson
-
BG/LM检验 (拉格朗日乘数检验)
DW检验有许多限制,只能用于阶序列相关性的检验,方程包含一个常数,而且方程不含滞后被解释变量,还有DW检验会随着被解释变量的个数增加,不确定区域也会扩大
- estat bgo
- estat bgo, lags(1/2)
- estat bgo, small lags(1/2)
- lags用来设置自相关系数
- Prob<0.05时拒绝原假设,认为存在自相关
- small specifies that the p-values of the test statistics be obtained using the F or t distribution instead of the default chi-squared or normal distribution.
自相关图和bg检验
estat bgodfrey, lags( p ) nomiss()
以上为BG检验原始语句,lags( p )用来指定BG检验的滞后阶数p,默认为lags(1),选择项nomiss()表示进行不添加0的BG检验,默认是以0代替缺失值,即DM方法
关于如何确认滞后阶数,简单的方法是看自相关图,画图自相关图后,阴影部分时95%的置信区间,点落在95%的置信区间之外或者附近,表明显著不为0,也就是有自相关
序列相关的补救之GLS方法
自动估计相关系数和阶数,两条命令代表相关系数的两种迭代方法
- prais Y X1 X2 X3
- prais Y X1 X2 X3, corc
序列相关的补救之NW方法
lag(3)代表最高自相关阶数为3
newey Y PC PB YD, lag(3)
异方差检验
参考博客
异方差的怀特检验
reg VOL TOT SAT // 先回归
estat imtest, white
异方差的补救
//补救措施1 怀特调整
reg PCON REG PRICE, robust
//补救措施2 变换方程形式(双对数)
gen lnPCON = ln(PCON)
gen lnREG = ln(REG)
gen lnPRICE = ln(PRICE)
reg lnPCON lnREG lnPRICE
//补救措施3 重新定义定义变量
gen PCON1 = PCON / POP
gen REG1 = REG / POP
reg PCON1 REG1 PRICE
例题
建立图书馆藏书量VOL对师生人数TOT,学生高考成绩SAT的回归模型,请写出线性回归模型的stata命令,采用white法检验异方差命令,采用White调整异方差的命令
reg VOL TOT SAT
estat imtest, white
reg VOL TOT SAT, robust
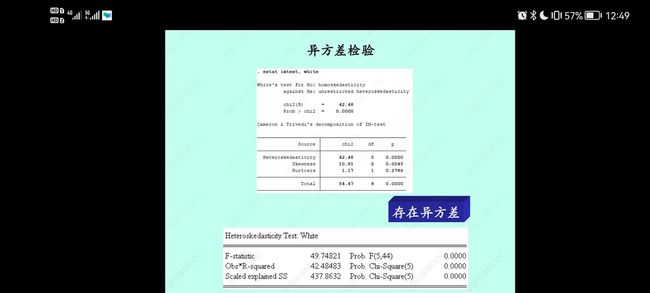
结果如下:
这个结果用的是CHICK6.dta的数据,但意思大同小异
怀特检验,我们主要H0是同方差假设,HA是异方差假设,看P值,如果P值<0.05说明我们要拒绝原假设,即原序列有着异方差性
怀特检验修正
画自相关图
ac e1
8A SAT互动练习
简单来说,本次练习就是寻找最合适的解释变量,来解释被解释变量。
首先肯定要选择GPA,APMATH以及APENG为我们的解释变量,然后AP因为APMATH以及APENG已经可以解释所以不用,然后看ESL和RACE因为样本中不是亚洲人就是白种人,如果英语不是母语,很大概率是亚洲人,并且在相关系数表中,ESL和RACE的相关系数为0.8461>0.8太大了,因此ESL和RACE只用选一个就可以了,在考试中我认为ESL个具有代表性,因为如果你不是母语者那么你学习过程中肯定有一定的困难,所以采用ESL作为解释变量,而GENDER和PEPR在我看来都有充足的解释力,而且前文也提到了性别对于SAT成绩的巨大影响。
综上所述,我们先用 GPA APMATH APENG ESL GENDER PEPR进行回归分析
预测符号
| 变量 | 符号 |
|---|---|
| GPA | + |
| APMATH | + |
| APENG | + |
| ESL | - |
| GEND | + |
| PREP | + |
开始回归
我们首先看系数与我们的设想一不一致,然后看p值,在t检验中,p值如果<0.05则说明该解释变量有显著的解释力,反之则没有。
我们发现PREP与我们的预期不符。表面上看,变量PREP是一个有影响力的变量,因为几乎可 以肯定PREP课程可以提高修读了该课程学生的SAT测试成绩。问题是学生修读PREP课程的 决定与他以前的(或者预期的)SAT测试成绩有关。我们相信那些感觉自己需要修读PREP课 程的学生会做出正确的判断,同时,我们认为这些课程会使他们的成绩达到与那些没有选修 PREP课程的学生的成绩不相上下。因而,该变量对SAT成绩没有显著的影响。
所以去除PREP
发现一个问题,其他变量p值都挺好的,但到了ESL就拉了,从感性角度出发,但是ESL有充分理由留在这里,这启发我们,数据统计出来的只是一个参考,具体问题,要结合具体的情况分析。
stata命令
- 导入数据
- 命令行 ——use “路径”
- 例:use “D:\stata\auto.dta”
- 标签——文件——打开——选择文件
- 命令行 ——use “路径”
- 计算函数
- exp()
- log()
- log10()
- sqrt()
- abs()
- 数据操作
- 导入数据
- 命令行——use “路径”
- 例:use “D:\stata\auto.dta”
- 标签——文件——打开——选择文件
- 命令行——use “路径”
- 删除数据行
- drop in 1/n //删除前n行
- drop in n 删除n行
- duplicates drop //删除重复行
- 导出dta文件为excel
- save name.dta, replace \ export excel using name
- 导入数据
- 变量操作
- 新建变量
- 命令行——generate 新变量名=新变量产生方法
- 例: generate newprice = price + 4(price是已有变量)
- 命令行——generate 新变量名=新变量产生方法
- 删除变量
- 命令行——clear
- 变量值排序
- 命令行——sort预排序变量
- 默认从小到大
- 例:sort price
- 命令行——sort预排序变量
- 查看变量值分布
- 命令行——tabulate 变量
- 变量的分组
- 命令行——generate 新变量 = autocode(旧变量,分类数,下界,上界)
- 举例
- generate newmpg = autocode(mpg, 3, 10, 40)
- 结果:新变量newmpg将只取20,30,40中的值
- 新建变量
- 矩阵操作
- 设置系统能容纳的矩阵大小
- 命令行: set matsize 数值
- 创建矩阵A
- 创建单位矩阵
- matrix define A = l(n) // 创建n维单位矩阵
- 创建单位矩阵
- 手动输入值构造
- Mat A=[1,2,3\4,5,6]
- 创建每个值相等的矩阵
- matrix A = J(行数,列数,每个元素的值)
- 通过变量构造
- mkmat 变量1 变量2 变量3,matrix(A) //会将三个变量作为矩阵的三列
- 通过矩阵构造
- matrix A = []//类似输入值构造,只不过换成了矩阵,注意行列对齐
- matrix A = 矩阵运算式
- matrix A = invsym(B)// B是一个可逆矩阵,A得到其逆矩阵
- matrix diag = vecdiag(A)//提取A的对角元素得到列向量diag
- matrix R = cholesky(A) // S = RR’,对S进行分解
- 创建对角矩阵
- mat D = diag(v) // 其中v是n * 1或 1 * n矩阵
- 显示矩阵A
- mat list A
- 提取矩阵某行某列
- X[1…2, 3…4]得到X第1、2行和第3、4列形成的矩阵
- X[1…, 3…]得到第1行到最后一行,第3列到最后一列
- 矩阵运算
- 取逆:invsym(A)
- 转置:A’
- 设计矩阵列名
- matrix colnames A = 第一列名 第二列名 第三列名
- 其他矩阵相关函数
- scalar m = rowsof(A)//返回矩阵A的行数给标量m
- scalar n = colsof(A)//返回矩阵A的列数给标量n
- 设置系统能容纳的矩阵大小
- 绘图
- 散点图
- Twoway scatter y x
- 折线图
- Twoway line y x
- 带数据点标记折线图
- twoway connected y x
- 垂直线图
- twoway dropline y x
- lowess图
- twoway lowess y x
- 脉冲图
- twoway spike y x
- 散点图
- 循环结构
- 见文档
- 得到data集中的所有行数
- scalar n = _N
- 单词表
- Obs(objects)有效观测样本
- Std.Dev(Standard deviation)标准差
- Wgt(Weight)权重
- Varlance方差
- Skewness偏度
- 用来衡量数据的不对称性
- <0时,概率分布左偏,有一个向左的尾
-
0时,概率分布右偏,有一个向右的尾
- =0时,数据相对均匀地排布在平均值两侧
- Kurtosis峰度
- 用来衡量数据的集中性
- 取值范围>=1,峰度值越大概率分布图越高尖
- 完全服从正态分布的数据峰度为3
- 统计、假设检验
- 查看变量的统计指标值
- 命令行——summarize [变量1 变量2 …][,detail]
- 后面不加变量名:输出所有变量的统计指标值
- 后面加变量名,变量名之间空格隔开:输出所选变量的统计指标值
- 例:summarize price mpg
- 后面加,detail:显示更多的统计指标值
- 例:summarize price mpg,detail
- 命令行——tabstat 变量1 [变量2 …],stats(指标1 [指标2 …])
- 命令行——summarize [变量1 变量2 …][,detail]
- 查看变量的统计指标值