函数与封装，分解和递归思想——C语言简明教程第2篇

0.封装与分解——为什么要创造函数

函数就是编程者自定义的一系列指令。

想象一下，a=2,b=3，你要交换整数a和b的值，怎么做呢？很简单，利用中介缓冲

int buffer=a;
a=b;
b=buffer;

c=1，d=5，你又要交换整数c和d的值，怎么做呢？同样的道理

buffer=c;
c=d;
d=buffer;

毫无难度。可是，如果你接下来还要交换q与w，e与r，t与y...的值呢？每次都把这步骤一模一样的三行再写一遍吗？或者说，这三两行的，你不在乎，那复杂些的功能呢？实现它需要数十上百个类似步骤呢？也再写一遍吗？

这时候，前辈们就想，能不能把这些步骤封装起来，我们只需要每次给它两个整数，它就会帮我们交换它们的值——其实类似的事情我们早已做过，没错，就是原语。我们用的C语言就是封装的产物，并且开发者帮我们定义了简便的封装方法，让我们也能定义自己的原语。

于是我们定义一个函数swap，每次给它需要交换的两个int变量的地址，它就会帮我们交换它们的值。

void swap(int*a,int*b){
int*mid;
*mid=*a;
*a=*b;
*b=*mid;}

封装，让我们对重复的操作，能简便地调用既定步骤，而不用再次思考和编写。就像一台空调，已经有人造出来了空调，我们就能方便地使用，而不需要知道它到底是怎么运行的，因为我们有它的操作面板。

封装的另一面就是分解。如果说封装是把一系列步骤打包成一个“黑盒子”，分解就是规划把哪些步骤打包成哪个“黑盒子”。

这就像写文章，我们先写一个大纲，把文章划分成好几部分，这部分说什么，那部分说什么，先把思路规划好，写作就会快很多。

写算法也一样，我们先把一个庞大的功能分解为几个大步骤，然后逐一实现这些大步骤，其中频繁使用的步骤就封装起来。

而函数就是封装成的那个“黑盒子”。

1.输入，执行和输出——函数在做什么

了解了封装和分解思想，我们对函数就有一个整体的把握了——函数是为了实现某个功能而创造的一系列步骤。但函数不仅仅包括这一系列步骤，它必须还有一个“操作面板”，我们借之告诉它，对哪些对象操作是什么、执行到什么程度、要产生什么结果等等信息。

就像为了控制室内气温，我们创造空调，但一台空调，绝不仅有制冷/热元件，还有开关按钮、调节温度按钮、模式转换按钮等等。

输入的“参数”就是函数的“控制面板”，返回值就是输出的结果，中间的一系列步骤，就是它的核心工作。

函数做的就是这个事情：接受参数，执行指令，返回结果。当然，熟练以后，你还可以整各种花活，比如不需要接受参数，每次调用都执行相同的指令；或者不返回结果，我们不需要它返回值，只需要它执行某些步骤。

注意，在接受参数以后，函数会开辟自己的变量空间，初始变量只有参数的复制品（注意，是复制品），以及全局变量。

所以除了全局变量以外，想要使用函数外变量，就必须把它作为参数传进去，函数外的变量它不认。同时，函数内部的变量与函数外无关，无论你在函数内部怎么变化传进去的参数复制品，函数外的参数本身都不会变化。当函数执行完毕时，它会产生一个返回值，作为函数的值，并释放其它的变量，你无法在函数执行完毕时再访问它们。

也就是说，输入和输出是函数内外变量交互的渠道。我们不用考虑函数内部变量是否与外界重名，也不用担心我们在函数内部变动参数，函数外也跟着变化。当函数执行完毕时，也不用担心内存占用，这些变量都会被释放。但这也是束缚，我们如果想通过函数去变化变量，只能通过传指针-改内存的方法进行。

当函数内部定义了一个变量与全局变量重名时，在该函数内部此全局变量失效，函数认自己创造的“亲儿子”。

在主函数内，调用的函数相当于其返回值。比如一个函数function(a,b,c)返回值是1，在主函数内就把它当成1，可以像1一样赋值、运算。

注意，它是一个值，字符、指针、结构体等等返回值（不可以是数组、字符串哦，因为函数输入与输出本质传的是指针，只能传仅用一个已知类型的指针能表达的东西。而数组和字符数组还需要长度），而不是一个指令。

比如你写了一个函数plus3，对传入整数参数+3并返回a+3

int plus3(int a){
a+=3;
return a;}

假如你在主函数中写int a=3;

plus3(a);

那么什么也不会发生，a还是a。这句话和

6;

对于主函数来说是一样的。我们得用同类型的变量去承接函数的返回值，比如可以

int b;

b=plus3(a);

需要用一个变量承接，让主函数和函数产生联系。或者传指针-改内存，我会在下一篇介绍，在这里就不展开了。

2.函数的定义

要使用函数，先要定义函数。

定义函数包括四个部分：定义函数类型（也就是函数返回值类型），定义函数名，定义参数类型和参数，定义执行指令。

举个例子，我们程序“正文”的第一行“int main（）”就是定义一个函数

int main(){

一系列执行语句..

return 0;}.

它的返回类型是整数，名字叫main，参数为无（实际上，是有参数的，不过编译器会帮你填好。这是多文件编程的内容，在这里当它不需要就行了）。在"{"和"}"中间是函数的执行指令集，函数依次执行大括号内的指令。最后一行语句"return 0"是它的返回值，无论你执行了什么，理论上它都应该返回0。

函数参数可以没有，也可以为1个或多个。没有参数也必须写上"()"，括号告诉编译器它是一个函数。若为多个，这些参数之间用","隔开，比如

(int argument 1,char argument 2,...,double argument n)

函数必须定义返回值类型，如果没有返回值，就是void类型。

3.函数的调用

和定义变量类似，函数定义的时候，必须前头写上函数类型，每个参数必须写上参数类型，但调用的时候，前头必须不写函数类型，参数必须不写参数类型。

直接通过函数名调用，在括号内输入参数，不要做多余的事情。

在调用它的地方，它相当于它的返回值。所以你可以把它当变量用，比如调用函数作函数参数。

同样的，可以在函数中调用函数。

4.递归——编程中的“数学归纳法”

分支和循环结构，大大拓展了我们的编程能力。而另一种结构——递归，也让算法编写的时候多了一种基本工具。

递归，就是在函数中调用它自己。

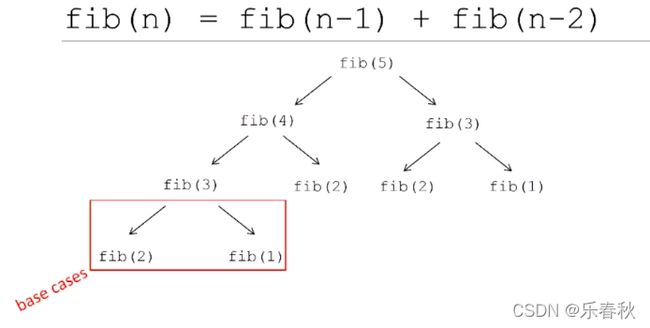
想象一种情况，我们要得到斐波那契数列第n个的值，怎么做？

学了控制流，我们能写出：

int fib(n){
int result;
if(n==1||n==2){
result=1;
}else{
int last=1;
int lala=1;
for(int i=3;i<=n;i++){
result=last+lala;
lala=last;
last=result;
}}
return result;}

但我们还有另一种写法——递归函数：

int fib(n){
if(n==1||n==2){
return 1;
}else{
returm fib(n-1)+fib(n-2);}}

十分简洁优美的写法，类似数学归纳法：我知道函数某个值，我知道函数不同输入之间值的推导关系，并且沿着这个推导方向，最终函数能走到那个已知的初始值。然后就像多米诺骨牌一样，层层推导，得到所求。

但，这个看起来简洁优美的递归法，效率并不高。比如求fib(4)时，我们先要求fib(3）,要求fib(3)，函数又调用自身求fib(2),fib(1)，最终相加得到fib(3)值为2，之后再调用fib(2)，得到1，再相加，得到fib(4)值为3。如果是fib(5)，计算量就更大了，除了按上述方法求fib(4)以外，还要再求一次fib(3)。

但fib(4)、fib(3)已经求过了啊，递归函数却不知道，会再求一次。

在python中，我们可以用“字典”结构解决这个问题，但在C语言中，我们并没有这种工具。若非要用一个数组承接已经求过的值，我们还得写动态分配内存方案，函数参数还得再加一个指针——如此复杂，还不如循环呢。

 

所以，递归法求值时，有些值会重复求很多次，随着递归次数增加，时间复杂度增长极快；不断开辟变量空间，创造参数副本，也浪费了大量内存空间。

一般情况下，循环结构人更难理解，但计算机更好执行；递归结构人易于理解，但计算机执行消耗巨大。这种时候尽量用循环。

不过，有些问题，循环无法解决，或者另一些问题，我们就是需要执行这些重复的步骤，这才是递归法的用武之地。

比如，著名的“汉诺塔”问题。

汉诺塔是一种益智玩具。它有三根相邻的柱子，标号为A,B,C，A柱子上从下到上按金字塔状叠放着n个不同大小的圆盘，要把所有盘子一个一个移动到柱子B上，并且每次移动同一根柱子上都不能出现大盘子在小盘子上方。下面这个动图就是一个示例。

现在，有一个小朋友想玩n阶汉诺塔，却不知道怎么操作。请写一个程序，打印出n阶汉诺塔的操作步骤，告诉小朋友怎么做。

似乎很困难。如果用控制流，它会十分复杂——我们不知道到底要执行多少步，所以最外层的大循环必然是while。我们还得有一个判断汉诺塔是否转移完成的标准，放在while循环的判断条件里。然后呢，在大循环里面如何操作？怎么把不同的n抽象成一个同样的循环步骤？...太复杂了，可能有方法能做出来，我没深入想下去，如果有大佬想出来了，可以开一个帖子发一下，在评论call我，我去观摩学习。

但是在递归的视角看来，这个问题却十分简单。我们先考虑二阶的情况：在A柱子上依次有两个圆盘，把它移动到B柱子上的步骤为

取A最上面的圆盘，放到C上

取A剩下的一个圆盘，放到B上

这时候，C上的圆盘比B上的小，直接取C上面的圆盘，放到B上，完成操作

容易总结出汉诺塔的思想：通过一个中介作缓冲，暂时容纳小圆盘，于是把大圆盘暴露在上面，从而得以把大圆盘放到目标柱子的最下面，然后在把小圆盘放到目标柱子上。

体会了中介缓冲的思想，就能显然得归纳：

1.已知n=2时的操作步骤

2.假设已知n=k时的操作步骤，对于n=k+1时，只需要

取A最上面k个圆盘，放到C上

取A剩下的那个圆盘，放到B上

取C上的k个圆盘，放到A上

由归纳假设，我们已知转移k个圆盘的步骤，所以我们也知道了n=k+1时的步骤。

综上，我们就知道了任意n>=2时的步骤，用代码实现如下

#include 

void HanoiTower(int n, char base, char goal, char buffer) {
	if (n == 2) {
		printf("from %c to %c\n", base, buffer);
		printf("from %c to %c\n", base, goal);
		printf("from %c to %c\n", buffer, goal);
	} else {
		HanoiTower(n - 1, base, buffer, goal);
		printf("from %c to %c\n", base, goal);
		HanoiTower(n - 1, buffer, goal, base);
	}
}

int main() {
	char base = 'A';
	char goal = 'B';
	char buffer = 'C';
	int n;
	scanf("%d", &n);
	HanoiTower(n, base, goal, buffer);
	return 0;
}

通过以上两个用例，相信你已经掌握递归的思想了，下面是练习，综合利用封装、分解和递归思想解决它吧：

把汉诺塔抽象成三个等长数组，

int a[n]={1,2,...,n};

int b[n]={};

int c[n]={};

1.当n=5时，把数组a中的数按汉诺塔的步骤，移动到数组b上

2.对于任意n，把数组a中的数按汉诺塔的步骤，移动到数组b上

如果你递归法以及掌握得很好了，并对字符串处理比较熟练，下面是蓝桥杯练习题：

 

注意审题，是输出表达式哦。

答案见下期