神经网络入门（二）

卷积神经网络

卷积神经网络（CNN）是一种具有局部连接、权重共享等特性的深层前馈神经网络．

1. 从全连接到卷积

卷积神经网络最早主要是用来处理图像信息．在用全连接前馈网络来处理图像时，会存在以下两个问题：

• 参数太多：在全连接前馈网络中，如果输入一张（100×100×3）的图片，第一个隐藏层的每个神经元到输入层都有 100 × 100 × 3 = 30 000 个互相独立的连接每个连接都对应一个权重参数．随着隐藏层神经元数量的增多，参数的规模也会急剧增加．这会导致整个神经网络的训练效率非常低，也很容易出现过拟合．

• 局部不变性特征：自然图像中的物体都具有局部不变性特征，比如尺度缩放、平移、旋转等操作不影响其语义信息．而全连接前馈网络很难提取这些局部不变性特征，一般需要进行数据增强来提高性能．

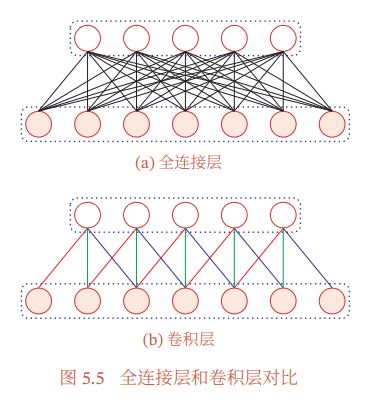
卷积层有两个很重要的性质：

1. 局部连接

在卷积层（假设是第 层）中的每一个神经元都只和下一层（第 − 1层）中某个局部窗口内的神经元相连，构成一个局部连接网络。

卷积层和下一层之间的连接数大大减少，由原来的 $M_l\times M_{l-1}$ 个连接变为 $M_l$ × 个连接， 为卷积核大小．

2. 权重共享

作为参数的卷积核${\mathbf{w}}^{(l)}$对于第 层的所有的神经元都是相同的．如图所示，所有的同颜色连接上的权重是相同的．

权重共享可以理解为一个卷积核只捕捉输入数据中的一种特定的局部特征．因此，如果要提取多种特征就需要使用多个不同的卷积核.

2. 卷积层

卷积是分析数学中一种重要的运算．在信号处理或图像处理中，经常使用一维或二维卷积．

2.1 一维卷积

一维卷积经常用在信号处理中，用于计算信号的延迟累积。

我们把 $w_1,w_2,\cdots$ 称为滤波器或卷积核．假设滤波器长度为，它和一个信号序列$x_1,x_2,\cdots$的卷积为
$$\begin{array}{rl}{y}_t& =w_1\times x_t+w_2\times x_{t-1}+\cdots +w_K\times x_{t-K+1}\\ & =\sum _{k=1}^K{w}_k{x}_{t-k+1}\end{array}$$

举个例子：

下层为输入信号序列，上层为卷积结果．连接边上的数字为滤波器中的权重．

（其中左边这幅图的结果为近似值）

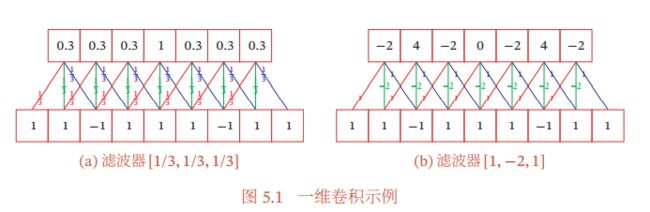
以右边这幅图的最左边的卷积结果为例，计算方式为：$1\times 1+1\times (-2)+(-1)\times 1=(-2)$

2.2 二维卷积

输入信息 和滤波器 的二维卷积定义为
$$\mathbf{Y}=\mathbf{W}\ast \mathbf{X}$$

• 其中∗表示二维卷积运算

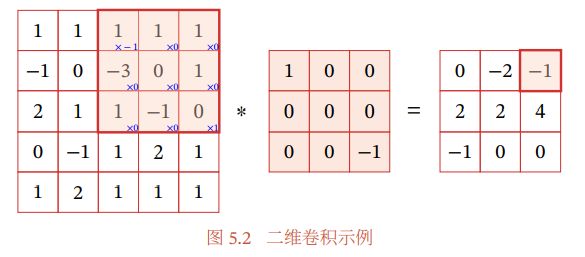
以下是一个二维卷积示例：

计算方式为：选取输入信息中与卷积核大小相等的一块，然后把卷积核180°翻转过来，再将此部分信息序列与卷积核中的数字一一对应乘积。

其中橘色区域的计算公式为：$1\ast (-1)+1\ast 0+1\ast 0+(-3)\ast 0+0\ast 0+1\ast 0+1\ast 0+(-1)\ast 0+0\ast 1=-1$

但是，在具体实现上，一般会以`互相关操作`来代替卷积，从而会减少一些不必要的操作或开销.

互相关和卷积的区别仅仅在于卷积核是否进行翻转．因此互相关也可以称为不翻转卷积．

公式可以表述为:

$$\mathbf{Y}=\mathbf{W}\otimes \mathbf{X}=\mathrm{rot}180(\mathbf{W})\ast \mathbf{X},$$

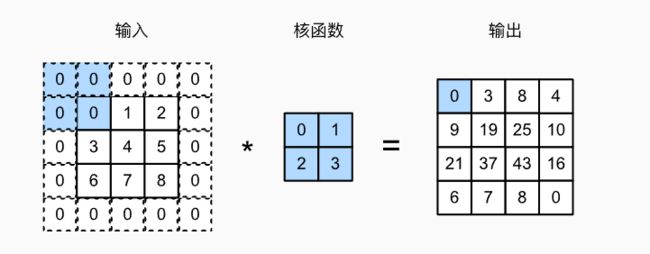
以下是一个互相关示例：

假设输入形状是 $n_h\times n_w$ ，卷积核窗口形状是 $k_h\times k_w$ ， 那么输出的形状将会是：
$$\left({\mathrm{n}}_{\mathrm{h}}-{\mathrm{k}}_{\mathrm{h}}+1\right)\times \left({\mathrm{n}}_{\mathrm{w}}-{\mathrm{k}}_{\mathrm{w}}+1\right)$$

3. 填充与步幅

填充

当卷积核尺寸大于 1 时，输出特征图的尺寸会小于输入图片尺寸。如果经过多次卷积，输出图片尺寸会不断减小。

为了避免卷积之后图片尺寸变小，通常会在图片的外围进行填充(padding)。

如下图所示，原输入高和宽的两侧分别添加了值为0的元素（padding=1)，使得输入高和宽从3变成了5，并导致输出高和宽由2增加到4。

如果在高的两侧一共填充 $p_h$ 行，在宽的两侧一共填充 $p_w$ 行，那么输出的形状将会是：

$$\left({\mathrm{n}}_{\mathrm{h}}-{\mathrm{k}}_{\mathrm{h}}+1\right)\times \left({\mathrm{n}}_{\mathrm{w}}-{\mathrm{k}}_{\mathrm{w}}+1\right)$$

步幅

目前我们看到的例子里，在高和宽两个方向上步幅均为1。我们也可以使用更大步幅，可以更灵活地进行特征抽取 。

下图为步幅为2的示例：

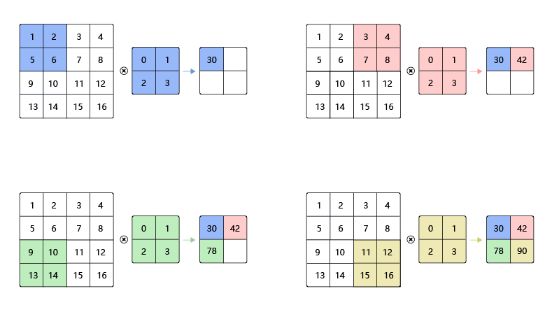
一般来说，当高上步幅为 $s_h$ ，宽上步幅为 $s_w$ 时，输出形状为

$$\lfloor \left({\mathrm{n}}_{\mathrm{h}}-{\mathrm{k}}_{\mathrm{h}}+{\mathrm{p}}_{\mathrm{h}}+{\mathrm{s}}_{\mathrm{h}}\right)/{\mathrm{s}}_{\mathrm{h}}\rfloor \times \lfloor \left({\mathrm{n}}_{\mathrm{w}}-{\mathrm{k}}_{\mathrm{w}}+{\mathrm{p}}_{\mathrm{w}}+{\mathrm{s}}_{\mathrm{w}}\right)/{\mathrm{s}}_{\mathrm{w}}\rfloor .$$

在实践中，通常有 $k_h=k_w$，$p_h=p_w$，$s_h=s_w$

因此：

• 填充可以增加输出的高和宽。这常用来使输出与输入具有相同的高和宽。
• 步幅可以减小输出的高和宽，例如输出的高和宽仅为输入的高和宽的 1 / n （n为大于1的整数）。
• 填充和步幅可用于有效地调整数据的维度。

4. 感受野

感受野(receptive field)是指感觉系统中的任一神经元，其所受到的感受器神经元的支配范围。

输入图像上 $k_h\times k_w$ 区域内每个元素数值的改变，都会影响输出点的像素值。我们将这个区域叫做输出特征图上对应点的感受野。

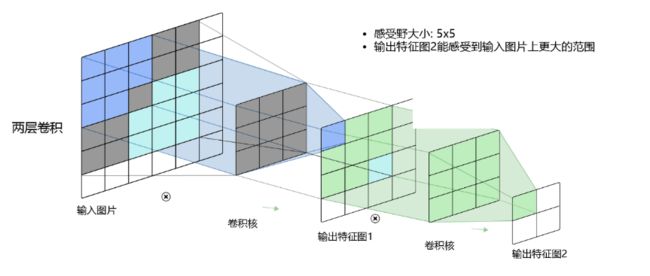
比如 3 × 3 卷积对应的感受野大小就是 3 × 3 。

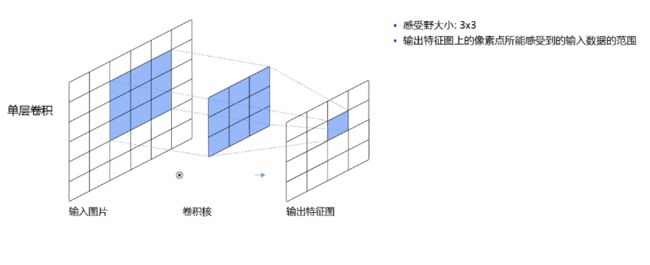
而当通过两层 3 × 3 的卷积之后，感受野的大小将会增加到 5 × 5 。

当增加卷积网络深度的同时，感受野将会增大，输出特征图中的一个像素点将会包含更多的图像语义信息。

5. 多输入多输出通道

在实际应用中，我们往往需要多输入和多输出通道的卷积核，例如彩色图像具有标准的RGB通道来代表红、绿和蓝。

当输入包含多个通道时，需要构造一个与输入数据具有相同输入通道数的卷积核，以便与输入数据进行互相关运算。

由于输入和卷积核都有 $c_i$ 个通道，我们可以对每个通道输入的二维张量和卷积核的二维张量进行互相关运算，再对通道求和（将 $c_i$ 的结果相加）得到二维张量。

举例：

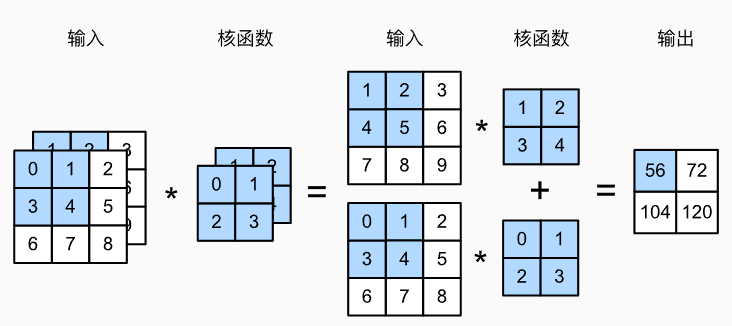
• 一个具有两个输入通道的二维互相关运算的示例。阴影部分是第一个输出元素以及用于计算这个输出的输入和核张量元素：

$$(1\times 1+2\times 2+4\times 3+5\times 4)+(0\times 0+1\times 1+3\times 2+4\times 3)=56$$

随着神经网络层数的加深，我们常会增加输出通道的维数，通过减少空间分辨率以获得更大的通道深度。

我们可以将每个通道看作对不同特征的响应，每个通道不是独立学习的，而是为了共同使用而优化的。

6. 池化层（汇聚层）

池化层，也称汇聚层、子采样层，其主用作用是进行特征选择，降低特征数量，从而减少参数数量，并获得更大的感受野。

作用： 降维 —— 特征选择和信息过滤。

池化层包含预设定的池化函数，其功能是将特征图中单个点的结果替换为其相邻区域的特征图统计量。使用某一位置的相邻输出的总体统计特征代替网络在该位置的输出，其好处是当输入数据做出少量平移时，经过池化函数后的大多数输出还能保持不变。

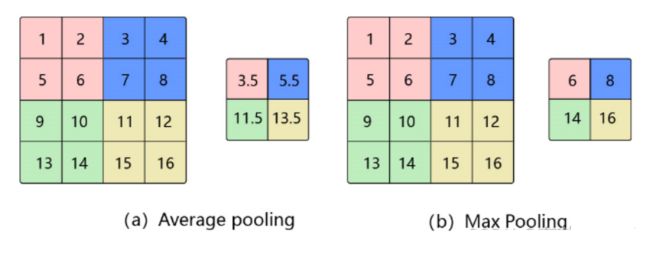
池化通常有两种：

平均池化：一般是取区域内所有神经元活性值的平均值

最大池化：选择这个区域内所有神经元的最大活性值作为这个区域的表示

7. 全连接层

作用：对提取的特征进行非线性组合以得到输出。

全连接层本身不具有特征提取能力，而是使得目标特征图失去空间拓扑结构，被展开为向量。

8. 卷积网络的整体结构

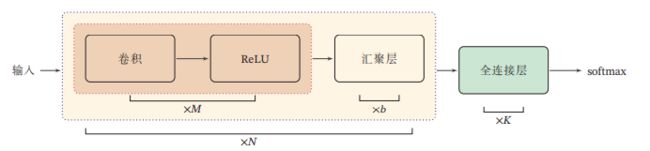
一个典型的卷积网络是由卷积层、汇聚层、全连接层交叉堆叠而成

一个卷积块为连续 个卷积层和 个汇聚层（ 通常设置为2 ∼ 5，为0或1）．

一个卷积网络中可以堆叠 个连续的卷积块，然后在后面接着 个全连接层（ 的取值区间比较大，比如 1 ∼ 100 或者更大； 一般为0 ∼ 2）．

目前，卷积网络的整体结构趋向于使用更小的卷积核（比如 1 × 1 和 3 × 3）以及更深的结构（比如层数大于 50）

9. 利用pytorch构建一个CNN网络

import torch
import torch.nn as nn
import torchvision.datasets as datasets
import torchvision.transforms as transforms
import torch.utils.data as data_utils
import cv2

# 数据集
train_data = datasets.MNIST(root="\mnist",train=True,transform= transforms.ToTensor(),download=True)
test_data = datasets.MNIST("mnist",train=False,transform=transforms.ToTensor(),download=True)

# 数据加载
train_loader = data_utils.DataLoader(dataset = train_data, batch_size = 64, shuffle = True)
test_loader = data_utils.DataLoader(dataset = test_data, batch_size = 64, shuffle = True)

# # 网络
class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv = nn.Sequential(
            nn.Conv2d(  # 卷积
                in_channels= 1, # 输入通道数（灰度图）
                out_channels=32,   # 输出的通道数（得到几个特征图）
                kernel_size=5,  # 卷积核大小
                padding=2,  # 外圈补零
                stride=1,	# 步长为1
            ),
            torch.nn.BatchNorm2d(32),   # 归一化
            torch.nn.ReLU(),    # 激活函数
            torch.nn.MaxPool2d(2), # 进行池化操作（2x2 区域）
        )
        self.fc = torch.nn.Linear(14*14*32,10)

    # len = batch_size / len(train_data) % batch_size
    def forward(self, x):
        out = self.conv(x)      # len*14*14*32
        out = out.view(out.size()[0],-1) # 164*6272
        out = self.fc(out)	# 64*10
        return out

cnn = CNN()	# 构建模型
cnn = cnn.cuda()	# 转到gpu运算
loss_fn = nn.CrossEntropyLoss()	# 交叉熵损失函数
optimizer = torch.optim.Adam(cnn.parameters(),lr = 0.01) # 使用Adam优化器

for epoch in range(10):
    for i, (images, labels) in enumerate(train_loader):
        image = images.cuda()
        label = labels.cuda()

        outputs = cnn(image)	# 将数据集放入神经网络中
        loss = loss_fn(outputs,label) # 计算损失函数

        optimizer.zero_grad()	# 梯度重新置为0
        loss.backward()	# 损失反向传播计算
        optimizer.step()	# 更新梯度