目标跟踪与定位学习笔记4-用于目标追踪的全卷积孪生神经网络

Fully- Convolutional Siamese Networks for Object Tracking

用于目标追踪的全卷积孪生神经网络

论文链接：arXiv

1. 概述

问题是跟踪视频中任意对象的问题，其中对象仅通过第一帧中的矩形来识别。虽然计算机视觉中的其他问题已经越来越普遍的采用的从大型监督数据集训练的深度卷积网络，但是监督数据的稀缺和实时操作的限制阻止了深度学习在每个视频学习一个检测器的范例的完美应用。

本文提出的方法在数十里现阶段训练深度卷积网络来解决更一般的相似性学习问题。然后在跟踪期间在线简单的评估该函数，本文的主要贡献是证明这种方法在现代跟踪基准中以远远超过帧速率要求的速度实现了极具竞争力的性能：1.训练一个孪生网络在更大的搜索图像中定位一个样本图像；2. 设计一种新颖的孪生体系结构，它相对于搜索图像是完全卷积的，通过计算其两个输入的互相关的双线性层来实现密集和有限的滑动窗口评估。

2. 用于跟踪的深度相似性学习

跟踪任意对象可以用样本相似性来解决，这里提出一个学习函数$f=(z,x)$，该函数将样本z与相同大小的候选图像x进行比较，如果两个图像描述了相同的对象，则返回高分，否则返回低分，为了找到物体在新图像中的位置，我们可以详尽地测试所有可能的位置，并选择与物体过去的外观最相似的候选位置。在实验中，我们将简单地使用对象的初始外观作为样本。函数f将从带有标记对象轨迹的视频数据集学习。

使用函数$f$来表示深度卷积网络。使用孪生网络来解决深度卷积网络中的相似性学习，孪生网络对两个输入应用相同的变换$\phi$，然后使用$f(z,x)=g(\phi (z),\phi (x))$，当g是简单的距离或相似性度量时，函数$\phi$可以被认为是嵌入。它以前被应用到诸如人脸验证、关键点描述读学习和一次性识别任务。

2.1 全卷积孪生网络架构

它对于候选图像是完全卷积的。为了进一步说明，使用$L_{\tau }$来表示平移算子$(L_{\tau }x)[u]=x[u-\tau ]$，函数h映射了信号到信号的带有整数步长k的全卷积网络，若
$$h(L_{k\tau })=L_{\tau }h(x)=h(x)[u-\tau ]$$
对任意转换$\tau$（当x是一个有限信号时只需要保持输出的有效区域）。

notes:

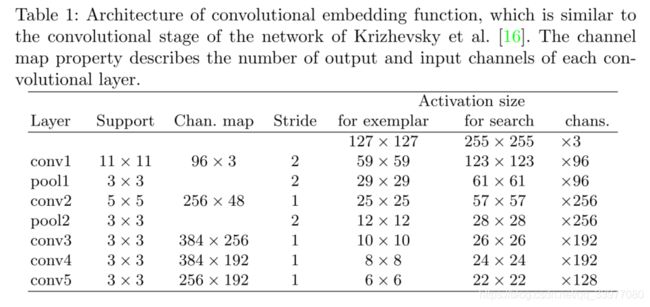
全卷积网络的优势在于，我们可以向网络提供更大的搜索图像作为输入，而不是相同大小的候选图像，并且它将在单次评估中计算密集网格上所有已转换子窗口的相似性。为了实现我们使用a convolutional embedding function$\phi$，并且使用a cross-correlation layer来组合这些结果特征图
$$f(z,x)=\phi (z)\ast \phi (x)+b1$$

其中，$b1$代表在每个位置取值$b\in \mathbb{R}$的信号有说法表示$b1$是得分图在每个位置的取值。这个网络的输出不是一个单一的score，而是在有限的网格$D\subset {\mathbb{Z}}^2$，值得注意的是，这个嵌入函数的输出是一个具有空间支持的特征图

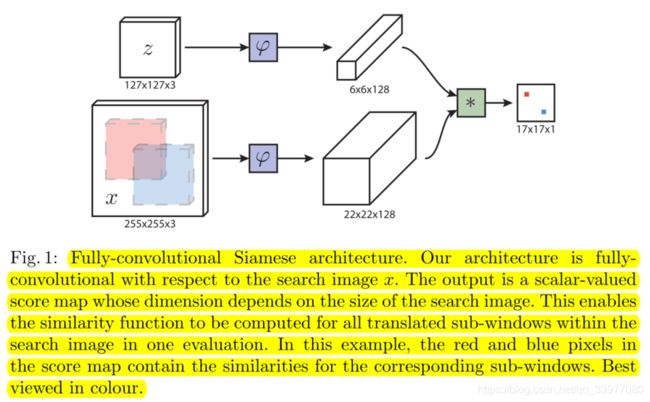
全卷积孪生网络，它与搜索图像x完全一致，输出是一个和搜索图像大小纬度相同的标量值的分数图，这使得能够在一次评估中为搜索图像内的所有翻译的子窗口计算相似性函数。在本例中，分数图中的红色和蓝色像素包含相应子窗口的相似性。最好用彩色观看。

跟踪过程中，使用以目标先前位置为中心的搜索图像。最大得分相对于得分图中心的位置，乘以网络的步幅，得到目标在帧与帧之间的位移。通过组合一个小批量的缩放图像，可以在一次向前传递中搜索多个缩放。

使用互相关和在较大的搜索图上一次评估网络合成特征图在数学上等同于在每一个已转换的子窗口使用内积和评估网络性能来合成特征图。然而，互相关层提供了一种简单的方法，可以在现有的卷积网络库的框架内有效的实现这一操作，不仅在测试中非常有用，同时也可以在训练中使用。

2.2 使用较大搜索图像训练

使用判别类方法，在正负样本中训练网络，计算损失函数：
$$\ell (y,v)=log(1+e^{-yv})$$

其中$v$是每个候选对在经过卷积操作的真实得分，y是真实值的标签，如果是同一类，得分越高，损失函数值越大，不同类y取-1，则得分越高，损失函数值越小，从优化的角度上来说，取最小值则可以得到最优解。在实验中取每一个位置的损失值的平均值。$y[u]$代表的是在u这小部分面积的x与z经过神经网络运算之后得到的map score。

其中$v$是单个样本候选对的真实值分数，$y\in \{+1,-1\}$是它的ground-truth标签。在训练中使用由样本图像z和大规模搜索图像x组成的对(pair)在我们的网络中开发一个全卷积网络。这会产生一个分数的映射对$v:\mathcal{D}\to \mathbb{R}$有效的生成每对的许多例子。定义得分图的损失为个体损失的平均值：
$$\begin{gathered} L(y,v)=\frac{1}{|\mathcal{D}|}\sum _{u\in \mathcal{D}}\ell (y[u],v[u]) \\ \frac{1}{|\mathcal{D}|}\sum _{u\in \mathcal{D}}log(1+e^{-y[u]\ast v[u]}) \end{gathered}$$
分数图中的每个位置$u\in \mathcal{D}$需要一个真正的标签$y[u]\in \{+1,-1\}$，而卷积网络中的$\theta$是通过对问题应用随机梯度下降(Stochastic Gradient Descent[SGD])得到的。
$$\arg \underset{\theta }{\min }\underset{z,x,y}{\mathbb{E}}L(y,f(z,x;\theta ))(5)$$
通过提取以目标为中心的样本和搜索图像，从带注释的视频数据集中获得配对。这些图像是从一个视频的两个帧中提取的，这两个帧都包含对象，并且最多相隔T帧。对象的类在训练期间被忽略。每个图像中对象的比例是标准化的，不会破坏图像的纵横比，若得分图的元素在中心的半径R内（考虑网络的步幅k），则它们被认为是正例。
$$y[u]=\{\begin{array}{l}+1ifk||u-c||\le R\\ -1otherwise.\end{array}$$
分数图中正反例的损失被加权以消除样本不平衡

从同一视频中提取的训练对:来自同一视频的样本图像和相应的搜索图像。当子窗口超出图像的范围时，丢失的部分用平均RGB值填充。

因为我们的网络是完全卷积的，所以不存在学习中心子窗口偏差的风险。我们认为，考虑以目标为中心的搜索图像是有效的，因为最困难的子窗口以及对跟踪器性能影响最大的子窗口很可能是与目标相邻的子窗口。

2.3 实际问题

数据集管理 在训练中，样本图像为127*127 pixels，搜索图像为255*255 pixels，图像被缩放，使得边界框加上用于上下文的附加边距具有固定的区域。更进一步，如果紧密边界框具有大小(w，h)，并且上下文余量是p，则选择缩放因子s，使得缩放矩形的面积等于常数
$$s(w+2p)\times s(h+2p)=A$$
使用样本图像的面积$A=127^2$并且将上下文量设置为平均维度$p=(w+h)/4$.每帧的样本和搜索图像都是离线提取的，以避免在训练过程中调整图像大小。

网络结构 在前两个卷积层之后使用最大池化，除了最后一层的conv5之外，其余的卷积层都是用了非线性的ReLU激活函数，在训练期间，每个线性层之后立即插入BN层. The stride of the final representation is eight. 设计的一个重要方面是网络中没有引入填充。

追踪算法 为证明全概率孪生网络的有效性及其在图像网络视频上训练时的泛化能力，使用一种及其简单的算法进行跟踪。不同于复杂的追踪器，不更新模型或保持对过去外观的记忆，不结合额外的线索，如光流或颜色直方图，不使用边界框回归来改进我们的预测。效果也比较好。

Online情况下我们结合了一些基本的时间约束：只在一个大约是以前大小四倍的区域内搜索对象，并在分数图上添加一个余弦窗口来惩罚大的位移。通过缩放空间的跟踪是通过处理搜索图像的几个缩放版本来实现的。比例的任何变化都会受到惩罚，当前比例的更新也会受到影响。

3. 孪生神经网络的细节

本部分参考CSDN大佬的文章，SiamNet: 全卷积孪生网络用于视频跟踪

对于搜索区域x，它的输出是一个得分图，所谓的得分就是相似度度量，得分图的维度是由搜索图像快决定的（样本模板和搜索区域进行密集交叉相关）。$\phi$代表的是一种特征映射操作，将原始图像映射到特定的特征空间。在论文，$\phi$是一个卷积嵌入函数，俗称==特征提取器==。其实是AlexNet的一部分只是把全连接层去掉而已。

作者采用判别式的方法对网络进行训练，更具体是采用正样本分别构成候选样本对(exemplar-candidate)来进行训练。上一帧的目标模板与下一帧的搜索区域可以构成很多对的候选样本对(exemplar-candidate pair)，但是根据判别式原理，近进下一帧的目标与上一帧的目标区域属于模型的正样本，其余大量的exemplar-candidate都是负样本，这样就完成了网络结构的端到端的训练。

损失函数的设计 损失函数模型本文采用判别式形式，即目标和搜索区域经过交叉互相关可以得到相关程度图谱，图像在训练过程中exemplar-candidate的准确关系是已知的，故设计损失函数并不困难。

• 很多研究通过使用预训练模型来解决上述问题。这些方法中，要么使用网络内部某一层作为特征的shallow方法（如相关滤波）；要么是使用SGD方法来对多层网络进行微调。然而shallow的方法没有充分利用端到端学习的益处，而使用SGD微调虽然能到达时最优结果，但却难以达到实时性的要求。
• 提出另一种替代性的方法。这个方法在初始离线阶段把深度卷积网络看成一个更通用的相似性学习问题，然后在跟踪时对这个问题进行在线的简单估计。这篇论文的关键贡献就在于证明这个方法在benchmark上可以达到非常有竞争性的性能，并且运行时的帧率远超实时性的要求。具体点讲，我们训练了一个孪生网络在一个较大的搜索区域搜索样本图片。本文另一个贡献在于，新的孪生网络结构是一个关于搜索区域的全卷积网络：密集高效的滑动窗口估计可通过计算两个输入的互相关性并插值得到。
• 跟踪任意目标的学习可看成是相似性问题的学习。我们提出学习一个函数 $f(x,z)$来比较样本图像 $z$ 和搜索图像 x 的相似性。如果两个图像描述的是同一个目标，则返回高分，否则返回低分。
• 我们用深度神经网络来模拟函数 $f$ 而深度卷积网络中相似性学习最典型的就是孪生结构。孪生网络对两个输入$z$ 和 $x$ 进行相同的变换 $\phi$ ，然后将得到的输出送入函数$g$ ，最后得到相似性度量函数为：$f(z,x)=g(\phi (z),\phi (x))$，其中$g$是一个简单的距离或相似度度量，$\phi$相当于特征提取器。

全卷积网络的优点是待搜索图像不需要与样本图像具有相同尺寸，可以为网络提供更大的搜索图像作为输入，然后在密集网格上计算所有平移窗口的相似度。本文的相似度函数使用互相关，公式如下
$$f(z,x)=\phi (z)\ast \phi (x)+b_1$$

• 1.$b1$表示在得分图中每个位置的取值
  2.上式可将 $\phi (z)$看成卷积核，在$\phi (x)$上进行卷积，相似度达的地方自然响应值就越大，那自然也就可以当做是目标z在x中的位置了。
• 跟踪时以上一帧目标位置为中心的搜索图像来计算响应得分图，将得分最大的位置乘以步长即可得到当前目标的位置

4. 具体实现

4.1 实现细节

训练过程 嵌入式参数是最小化公式5得到的。使用MatConvNet进行简单的SGD[31]。参数的初始值遵循高斯分布，根据改进的Xavier方法缩放[32]。训练在50个epoch内进行，每个时期由50000个样本对组成(根据sec。2.2).每次迭代的梯度使用大小为8的batch进行估计，学习速率在每个时期从$10^{-2}$到$10^{-5}$进行几何退火。

追踪时期 在线的阶段是可以减小规模，开始物体特征$\phi (z)$会被计算一次，并会和后续帧的子窗口进行卷积比较。通过简单的策略（线性插值）在线更新（样本的特征表示）不会获得太多性能。使用双三次插值从17*17到227*272队得分图进行上采样会导致更精确的定位，因为原始图相对粗糙。为了处理规模变化，我们通过五个规模$1.025^{\{-2,-1,0,1,2\}}$来搜索目标，并且通过带有参数为0.35的线性插值来更新规模以便提供衰减。

为使实验具有重复性，在http://www.robots.ox.ac.uk/~luca/siamese-fc.html共享了训练和跟踪代码，以及生成精选数据集的脚本。在一台配备了单个NVIDIA GeForce GTX Titan X和4.0GHz英特尔酷睿i7-4790K的机器上，当分别在3和5个比例上搜索时，我们的完整在线跟踪管道以每秒86帧和58帧的速度运行。

4.2 评估

我们评估了我们简单跟踪器的两个变体:Siamfc(Siamese fully Convolulative)和SiamFC-3s，它在3个尺度上而不是5个尺度上搜索。

4.3 OTB-13基准

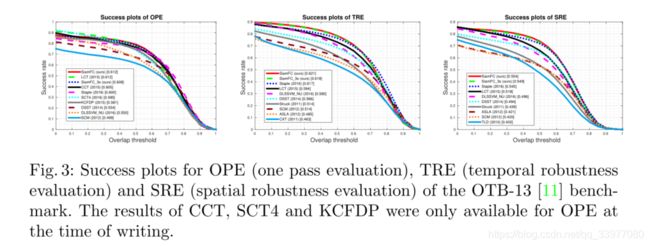
OTB-13¹考虑了不同阈值下平均每帧的成功率：如果跟踪器的估计值和ground-truth之间的IoU高于某个阈值，则跟踪器在给定帧是成功的。然后根据不同阈值的成功率曲线下的面积来比较跟踪器。除了[11]报道的跟踪器之外，在图3中，我们还比较了在主要计算机视觉会议上出现的七种更先进的跟踪器，它们可以以帧速率运行:Staple [33]、LCT [34]、CCT [35]、SCT4 [36]、DLSSVM NU [37]、DSST [38]和KCFDP [39]。给定序列的性质，对于这个基准，在训练期间我们只将25%的对转换成灰度。所有其他超参数(用于训练和跟踪)都是固定的。

4.4 VOT基准

在我们的实验中，我们使用了视觉对象跟踪(VOT)工具包(标签vot2015-final)的最新稳定版本，该工具包对从356个序列池中选择的序列上的跟踪器进行评估，选择这些序列是为了很好地表示七种不同的挑战情况。许多序列最初出现在其他数据集中(例如ALOV [1]和OTB [11])。在基准测试中，跟踪器在故障后五帧自动重新初始化，这被认为是在估计的边界框和地面真实值之间的IoU变为零时发生的。

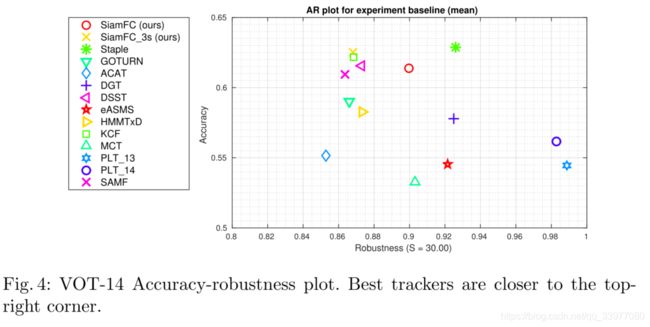
VOT-14 的准确度和鲁棒性结果：Staple和GOTURN为CVPR和ECCV 2016上展示的两个实时跟踪器。准确性以平均IoU表示，鲁棒性以故障总数来表示。

VOT-15的度量结果：本文还与2015年的40个最佳版本进行比较，在此情况下计算期望平均重叠度使用原始数据的准确率和失败用例的个数来衡量。它代表失败后没有重新初始化的平均IoU。下图表示VOT-15中表现较为优异的40个跟踪器。

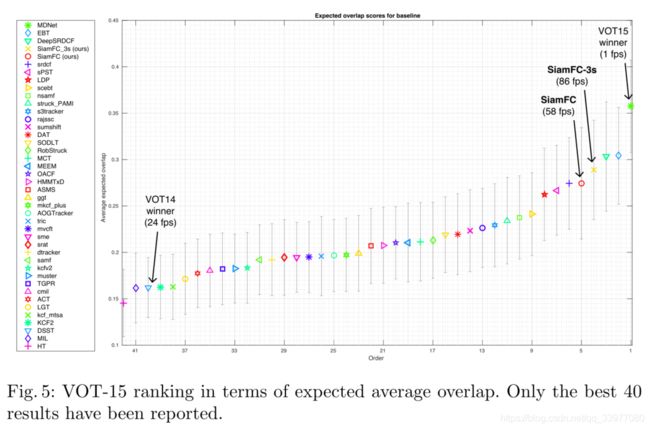
尽管简单，我们的方法比最新的实时跟踪器有所改进(图3和4)。此外，它在具有挑战性的VOT-15基准中优于大多数最好的方法，同时是唯一一个达到帧速率的方法(图5和表2)。这些结果表明，仅在ImageNet Video上，我们的全卷积孪生网络学习的相似性度量的表达能力就足以获得非常强的结果，与最新的技术方法相当或更好，后者通常慢几个数量级。我们相信，通过使用跟踪社区经常采用的方法(例如，模型更新、边界框回归、微调、记忆)来扩充最低限度在线跟踪管道，可以获得相当高的性能。

我们提出的方法的原始分数、重叠和报告的速度，以及VOT 15人挑战赛中表现最佳的15名跟踪者。在可行的情况下，我们与作者报告的速度进行比较，否则(*)我们以EFO单位报告VOT-15结果[12]的值，该值大致相当于每秒钟(例如，NCC跟踪器的速度是每秒钟140英尺，EFO是每秒钟160英尺)。

4.5 数据集介绍

下表说明用于训练乱神网络的数据集大小如何极大地影响性能。当数据集的大小从5%增加到100%时，预期的平均重叠(在onVOT-15上测量)从0.168稳步提高到0.274。这一发现表明，使用更大的视频数据集可以进一步提高性能。事实上，即使200万个受监督的包围盒看起来是一个巨大的数字，但不应该忘记，它们仍然属于数量相对适中的视频，至少与通常用于训练conv网络的数据量相比是如此。

5. 结论

在这项工作中，我们脱离了传统的在线学习方法，并展示了一种替代方法，侧重于在离线阶段学习强嵌入。与它们在分类设置中的使用不同，我们证明了对于跟踪应用程序，孪生全虚拟深度网络能够更有效地使用可用数据。这既反映在测试时，通过执行有效的空间搜索，也反映在训练时，其中每个子窗口有效地表示有用的样本，几乎没有额外的成本。实验表明，深度嵌入为在线跟踪器提供了自然丰富的功能来源，并使简单的测试时策略能够很好地执行。我们认为，这种方法是对更复杂的在线跟踪方法的补充，并期望未来的工作能够更彻底地探索这种关系。

简单跟踪器的快照。配备了我们提出的在ImageNet视频上从头开始训练的全卷积孪生网络。方法中不执行任何模型的更新，所以它只使用第一帧来计算$\phi (z)$.尽管如此，它对许多具有挑战性的情况，如运动模糊(第2行)、外观的剧烈变化(第1、3和4行)、照明不佳(第6行)和比例变化(第6行)，都具有惊人的鲁棒性。另一方面，我们的方法对混乱的场景很敏感(第5行)，可以说是因为模型从不更新，因此互相关对所有与目标的第一次出现相似的窗口给出了很高的分数。

---

1. Wu, Y., Lim, J., Yang, M.H.: Online object tracking: A benchmark. In: CVPR 2013. (2013) ↩︎