鸢尾花分类预测实验（机器学习）

鸢尾花数据集的分类预测实验是机器学习最经典的案例之一，通过模型的训练，对于大量的鸢尾花数据集的学习，可以识别出新的鸢尾花是什么类型，继而完成预测和分类

鸢尾花的分类和预测大概分为如下几个步骤

（1）准备训练数据     （2）切分数据集         （3）数据归一化/标准化（对其正态分布转化）（4）对数据集的训练和预测（多轮交叉验证）    （5）验收结果

1） 准备训练数据

#鸢尾花数据集加载
iris=datasets.load_iris()
X=iris.data[:,2:]#数据采用花瓣长和宽
y=iris.target  #类别数据

2）切分数据集

#交叉验证 切分数据集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=0)

X_train:训练集    X_test:测试集       y_train:鸢尾花类别的训练集    y_test:鸢尾花类别的训练集      X,y是要进行划分的数据集               test_size:测试集所占的比例（若为正数则为测试的数量）     random_state：随机数的种子（后面的数字只要是同一个，所产生的随机数就固定，但是不同的随机数种子所对应的随机数不一样）

train_test_split是切分数据集的函数

3）数据归一化处理/标准化（正态分布转化）

在机器学习中，偏好于0-1之间的数字，更偏好于正态分布的数据集，因此将数据集转化为正态分布，更有利于减小误差

归一化的作用和意义：归一化可以最大程度的去除极大值和极小值的边缘值对于数据的影响，将数据转化为符合正态分布的数据

#数据归一化处理
from sklearn.preprocessing import MinMaxScaler   #最值归一化
from sklearn.preprocessing import StandardScaler  #均值方差归一化
standardScaler=StandardScaler()
standardScaler.fit(X_train)#得到原始数据特征值的均值和方差  拿参数
X_train_avg=X_train.mean()
X_train_var=X_train.var()
#均值
print(X_train_avg[:,0])
print(X_train_avg[:,1])
#方差
print(X_train_var[:,0])
print(X_train_var[:,1])
X_train_std=standardScaler.transform(X_train)
X_test_std=standardScaler.transform(X_test)

求每一列平均值和方差除了上述的方式外还有两种

其中axis=0表示一列一列从左向右推进，axis=1表示一行一行从上往下推进，但是如果要用for循环，过程就比较繁琐，这也是numpy的优势之一 

MinMaxScaler是一种常用的归一方式，

MinMaxScaler和StandardScaler的区别：归一化主要是为了将数据映射到0~1的范围内，将有量纲的表达式变成无量纲的，化为纯量，消除了由于特征加持下对于数据的一些影响，使各个特征数据对于目标的影响权重是一样的，而标准化则不然，标准化依旧保持了数据原有的特征信息，类似于是等比例的转化，对不同特征维度的伸缩变换的目的是使得不同度量之间的特征具有可比性。同时不改变原始数据的分布(并未使数据集转到0~1之间)

下面用图形来表示

在对训练数据进行标准化后，我们在本次的示例中使用标准化（标准化往往优先于归一化）来处理数据，之后开始训练数据

standardScaler=StandardScaler()
standardScaler.fit(X_train)

 对于不同的函数，我们所需要的参数不一样，，训练模型可以看作是拿参数，在我们下面写的标准化训练集和测试集中就会用到，不同的模型和函数所需要用到的参数不同

4）对数据集的训练和预测（多轮交叉验证）

我们在对于模型的参数进行赋值时，有时候一开始所写的参数与最佳参数相差较大，不能完美拟合，如何寻找最合适的参数成了我们最需要解决的问题

例如本示例中：

我们最初输入的数据，精度和拟合效果并不好，因此我们需要不断的进行交叉验证，确定合适的参数，也可以利用网格搜索的方法，来确定最好的参数组合

一次一次的训练，效率未免 有些低，我们可以采用多次交叉验证的方式来实现

我们通过cross_val_score来实现多次的交叉训练,下面我们对cross_val_score的参数进行分析，sklearn.model_selection.cross_val_score(estimator, X, y=None, groups=None, scoring=None, cv=’warn’, n_jobs=None, verbose=0, fit_params=None, pre_dispatch=‘2*n_jobs’, error_score=’raise-deprecating’)

estimator： 需要使用交叉验证的算法
X： 输入样本数据
y： 样本标签                                                                                                                           cv： 交叉验证折数或可迭代的次数
groups： 将数据集分割为训练/测试集时使用的样本的组标签（一般用不到）
scoring： 交叉验证最重要的就是他的验证方式，选择不同的评价方法，会产生不同的评价结果
n_jobs： 同时工作的cpu个数（-1代表全部）
verbose： 详细程度
fit_params： 传递给估计器（验证算法）的拟合方法的参数
pre_dispatch： 控制并行执行期间调度的作业数量                                               error_score： 如果在估计器拟合中发生错误，要分配给该分数的值（一般不需要指定）

还有一个点：我们在之前对于模型的精确度测试时，需要对模型进行训练

knn_clf=KNeighborsClassifier(n_neighbors=5)
knn_clf.fit(X_train_std,y_train)#训练
knn_clf.score(X_test_std,y_test)

但是多次交叉验证函数，不需要再额外的写训练函数，已经内置在其函数内部

knn_clf1=KNeighborsClassifier(n_neighbors=6)
scores=cross_val_score(knn_clf1,X_std,y,cv=5)

接下来我们对于训练矫正好的模型进行一次实际的分类预测

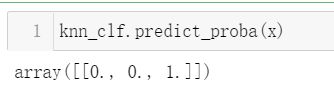
在进行预测时，knn_clf.predict()函数，输入的变量x一定要是一个二维数组，不能是一维数组，因为我们的训练集是一个二维数组，要保持形式的一致

我们每一朵新的鸢尾花，他的分类有三种可能，具体是哪一个，我们也可以通过函数求得，来得出新的鸢尾花数据点为各类别的概率大小，需要注意的是，相关点的概率之和应该等于1，一个点的几种概率之和也应该等于1。

#分类边界
#X只有两个特征
def plot_decision_boundary(model,X,y):   #划边界
    x0_min,x0_max=X[:,0].min()-1,X[:,0].max()+1
    x1_min,x1_max=X[:,1].min()-1,X[:,1].max()+1
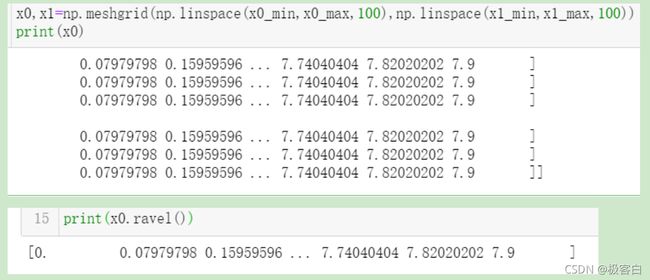
    x0,x1=np.meshgrid(np.linspace(x0_min,x0_max,100),np.linspace(x1_min,x1_max,100))
    Z=model.predict(np.c_[x0.ravel(),x1.ravel()])
    Z=Z.reshape(x0.shape)
    
    plt.contourf(x0,x1,Z,camp=plt.cm.Spectral)
    plt.ylabel('x1')
    plt.ylabel('x0')
    plt.scatter(X[:,0],X[:,1],c=np.squeeze(y))
    plt.show()
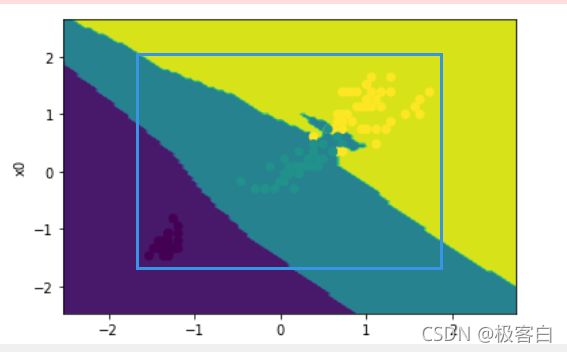
plot_decision_boundary(knn_clf,X_train_std,y_train)

当我们昨晚预测之后，就要整体的把我们的模型和实例的分类装框用图像的形式画出来，因此我们此时就应该对图像进行分类边界处理

我们在此定义一个函数  plot_decision_boundary()来对于鸢尾花数据点来进行分类和划界

x0_min,x0_max=X[:,0].min()-1,X[:,0].max()+1
x1_min,x1_max=X[:,1].min()-1,X[:,1].max()+1

这两处是为了对于整体范围进行划定，便于我们进行观察

 +1和-1就是为了是我们所观察的蓝框区域的大小做出相应的改变

 x0,x1=np.meshgrid(np.linspace(x0_min,x0_max,100),np.linspace(x1_min,x1_max,100))
 Z=model.predict(np.c_[x0.ravel(),x1.ravel()])
 Z=Z.reshape(x0.shape)
    
 plt.contourf(x0,x1,Z,camp=plt.cm.Spectral)
 plt.ylabel('x1')
 plt.ylabel('x0')
 plt.scatter(X[:,0],X[:,1],c=np.squeeze(y))
 plt.show()

 np.meshgrid()用来构建网格矩阵

网格矩阵就是在方格纸上画出坐标系找出对应矩阵的大概范围

np.linspace(起点，终点，要建立的点数的个数)   #这种方式建立的是均匀的间隔

类似的还有一个函数也可以实现类似的功能  

range(start,stop,step)#start:计数从start开始，默认是从0开始；stop：计数到stop结束，但是不包括 stop；step：步长，默认为1

np.meshgrid()的具体用法，np.meshgrid(数据集点的x坐标集合，数据集点的y坐标集合)

具体理解：在坐标系中，有很多个点，每个点有x、y坐标，我们将每个点的x坐标和y坐标分装到两个集合中，我们使用np.meshgrid可以将x坐标集合扩展成x行y列，每一行的数组都相同，将y坐标集合扩展成x行y列，每一列的坐标相同，这样其实就得到了x，y坐标组成的网格矩阵也就是我们常用的平面直角坐标系，但是现在我们的x，y已经变成了所谓“矩阵体”若想要将其最基本的单元剥离出来，则要用到numpy.ravel函数，这个函数可以将重复的行或列压缩成一行或一列最简单的“单元数组”

 但是仅仅将它们抽离开还并不能满足我们的需求，我们需要根据x0_ravel,x1_ravel两组数据来确定我们预测的这一莺尾花数据点为哪一类别，所以我们应该将两组数据按列连接。注意，一定是只有两组数据时才会按列连接(并且，列数还要相同）,如果是三组数据，便不会出现列连接，而是行连接，甚至是直接变成一维数组，例如：

与此同时，我们在为了使用的视觉舒适度上，如果将这100×100的数据集直接输出，我们不容易看出哪一个坐标点的数据集所对应的类别，但是如果将类别的统计的结果也做成一个100×100的矩阵，呈现程度会好很多，我们只需要改变输出的类别数据集的形状即可

Z=model.predict(np.c_[x0.ravel(),x1.ravel()])
Z=Z.reshape(x0.shape)

我们来总结和梳理一下分类划线的整个逻辑：

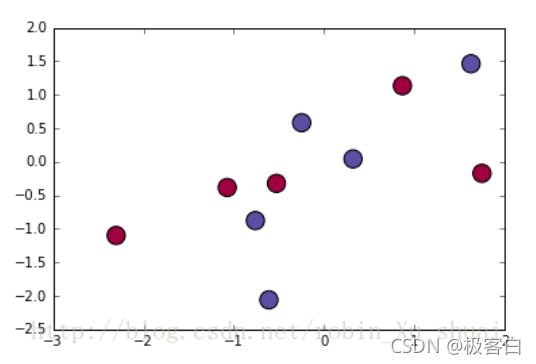
为了使得我们现有的训练集的数据更加泛化，我们将数据点的x，y坐标集进行均匀的打散，又根据predict函数预测出被打散后的坐标点所属的类别，再利用，x,y,类别信息进行作图，会形成三色分层的类别图像，分层处即为等高线，在此处应用了plt.contourf函数（用于绘制等高线），在进行完分层操作后，我们再将我们所应用到的散点以散点图的形式借助plt.scatter的函数呈现出来，这样做的好处是，通过观察散点所处的颜色分层，可以清楚地知道该数据集点所属的类别

接下来是对于函数的细节进行解析

coutour(X,Y,Z,**kwargs)

X:横坐标，Y纵坐标，Z分类的类别结果，**kwarge：一些必要的参数信息（示例中为分层的颜色信息）  PS：当 X,Y,Z 都是 2 维数组时，它们的形状必须相同。如果都是 1 维数组时，len(X)是 Z 的列数，而 len(Y) 是 Z 中的行数。在示例中我们还有一个参数，camp=plt.cm.Spectral为不同的数据坐标 点 进行随机分配颜色

例如：

plt.ylabel('x1')
plt.ylabel('x0')

#plt.ylabel  是设置y轴标签文本的函数，plt.xlabel  是设置x轴标签文本的函数，在当前这个例子中，x轴标签文本是x0，y轴的标签文本是x1

plt.scatter(X[:,0],X[:,1],c=np.squeeze(y))

这行代码涉及到了画散点图，在此我们对scatter函数进行分析（）

matplotlib.pyplot.scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None, vmin=None, vmax=None, alpha=None, linewidths=None, verts=None, edgecolors=None, *, data=None, **kwargs)

x，y：表示的是大小为(n,)的数组，也就是我们即将绘制散点图的数据点

s:是一个实数或者是一个数组大小为(n,)，这个是一个可选的参数。

c:表示的是颜色，也是一个可选项。默认是蓝色'b',表示的是标记的颜色，或者可以是一个表示颜色的字符，或者是一个长度为n的表示颜色的序列等等。但是c不可以是一个单独的RGB数字，也不可以是一个RGBA的序列。可以是他们的2维数组（只有一行）。

marker:表示的是标记的样式，默认的是'o'。

cmap:Colormap实体或者是一个colormap的名字，cmap仅仅当c是一个浮点数数组的时候才使用。如果没有申明就是image.cmap

norm:Normalize实体来将数据亮度转化到0-1之间，也是只有c是一个浮点数的数组的时候才使用。如果没有申明，就是默认为colors.Normalize。

vmin,vmax:实数，当norm存在的时候忽略。用来进行亮度数据的归一化。

alpha：实数，表示的是透明度，值域在0-1之间。

linewidths:也就是标记点的长度。

而我们示例中的c（颜色选项）c=squeeze（y）

np.squeeze函数的作用，我们用几个实例来理解一下

np.squeeze可以理解成是维数简化

3维的简化成2维的，2维的简化成1维的，1维的不变

knn_clf=KNeighborsClassifier(n_neighbors=78)
knn_clf.fit(X_train_std,y_train)#训练
plot_decision_boundary(knn_clf,X_train_std,y_train)

上图就是属于拟合失败的情况，模型没有学明白 

 我们之前设置的k邻近型分类器的临近数据点数设为30，但是我们这个参数不一定每次都能够精确找到，那如何能够找到那个最合适的参数是一个问题，因此我们需要通过进行拟合检测来找到最符合我们建立模型的临近节点数值

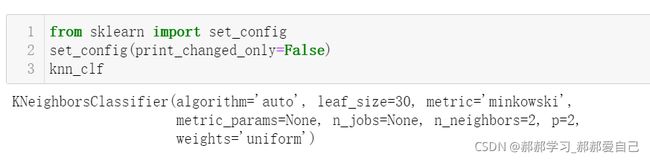
 set_config指的是  设置全局的scikit-learn的配置

set_config(print_changed_only=False)

print_changed_only的值如果为True，则跳过对有限性的验证，节省了时间，但也导致了潜在的崩溃。如果print_changed_only的值为False，将执行有限性验证，避免错误。全局默认值:False。

如果想要了解具体参数的意义，参照我往期的博客   《 K近邻算法（机器学习）》

我们通过机器学习就是为了得到一个较为精确的分类器模型能够对鸢尾花进行一个相对于精确的分类，许多参数如果只靠人为的摸索调参，效率就太低了，因此我们在面对  较小的数据集时可以采取GridSearchCV这一调参利器来实现

GridSearchCV，它存在的意义就是自动调参，只要把参数输进去，就能给出最优化的结果和参数。但是这个方法适合于小数据集，一旦数据的量级上去了，很难得出结果。

现在来对于GridSearchCV的参数意义进行说明

class sklearn.model_selection.GridSearchCV(estimator, param_grid, scoring=None, fit_params=None, n_jobs=1, iid=True, refit=True, cv=None, verbose=0, )

 estimator：选择使用的分类器

param_grid：需要最优化的参数的取值，值为字典或者列表

 scoring=None：模型评价标准，默认None,这时需要使用score函数

 fit_params=None

n_jobs=1 ：n_jobs: 并行数，int：个数,-1：跟CPU核数一致, 1:默认值

iid=True ：iid:默认True

 cv=None ：交叉验证参数，默认None，使用三折交叉验证。指定fold数量，默认为3

verbose=0, scoring=None

verbose：日志冗长度，int：冗长度，0：不输出训练过程，1：偶尔输出，>1：对每个子模型都输出

 我们本案例中

param_grid=[
    {
#         range(start, stop [,step]) 
        'weights':['uniform'],
        'n_neighbors':list(range(1,11))
    },
    {
        'weights':['distacne'],
        'n_neighbors':list(range(1,11)),
        'p':list(range(1,6))
    }
]

param_grid之所以分成两部分，是因为想看一下是均匀权重下还是在不均等权重下拟合程度更好，从而得出更精确的参数，但是小编在此有个疑问，p所表示是距离度量公式，而度量公式只有两种，当p=1时，为曼哈顿距离公式，p=2时为欧式度量公式，所以p的值为什么要在（1-6之间）去索引除此之外小编还疑惑一件事，是不是只有在distance的权重分配模式下才涉及到距离度量公式？希望大佬们可以解答一下我的困惑，一起进步共同学习。

5）验收结果

最后我们来看一下我们通过GridSearchCV校准好的分类器模型的各项参数和性能