% clc;
close all;clear all;
p=[ 1739.94 1675.15 2395.96
373.3 3087.05 2429.47
1756.77 1652 1514.98
864.45 1647.31 2665.9
222.85 3059.54 2002.33
877.88 2031.66 3071.18
1803.58 1583.12 2163.05
2352.12 2557.04 1411.53
401.3 3259.94 2150.98
363.34 3477.95 2462.86
1571.17 1731.04 1735.33
104.8 3389.83 2421.83
499.85 3305.75 2196.22
2297.28 3340.14 535.62
2092.62 3177.21 584.32
1418.79 1775.89 2772.9
1845.59 1918.81 2226.49
2205.36 3243.74 1202.69
2949.16 3244.44 662.42
1692.62 1867.5 2108.97
1680.67 1575.78 1725.1
2802.88 3017.11 1984.98
172.78 3084.49 2328.65
2063.54 3199.76 1257.21
1449.58 1641.58 3405.12
1651.52 1713.28 1570.38
341.59 3076.62 2438.63
291.02 3095.68 2088.95
237.63 3077.78 2251.96
1702.8 1639.79 2068.74
1877.93 1860.96 1975.3
867.81 2334.68 2535.1
1831.49 1713.11 1604.68
460.69 3274.77 2172.99
2374.98 3346.98 975.31
2271.89 3482.97 946.7
1783.64 1597.99 2261.31
198.83 3250.45 2445.08
1494.63 2072.59 2550.51
1597.03 1921.52 2126.76
1598.93 1921.08 1623.33
1243.13 1814.07 3441.07
2336.31 2640.26 1599.63
354 3300.12 2373.61
2144.47 2501.62 591.51
426.31 3105.29 2057.8
1507.13 1556.89 1954.51
343.07 3271.72 2036.94
2201.94 3196.22 935.53
2232.43 3077.87 1298.87
1580.1 1752.07 2463.04
1962.4 1594.97 1835.95
1495.18 1957.44 3498.02
1125.17 1594.39 2937.73
24.22 3447.31 2145.01
1269.07 1910.72 2701.97
1802.07 1725.81 1966.35
1817.36 1927.4 2328.79
1860.45 1782.88 1875.13
];
[num,n]=size(p); %样品数目
centernum=4; %类别数目
IDXO=[1 2 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 ];
% size(IDXO)
CO(1,:)=[ 1739.94 1675.15 2395.96];
CO(2,:)=[373.3 3087.05 2429.47];
CO(3,:)=[1756.77 1652 1514.98];
% s1=find(IDXO==1);%聚类号为1的样品在p中的序号
% s11=p(s1,:)
s4=find(IDXO==4);%聚类号为4的样品在p中的序号
s44=p(s4,:);%全部为4类的样品矩阵
CO(4,:)=[sum(s44(:,1))/59,sum(s44(:,2))/59,sum(s44(:,3))/59];%第4类的中心
JO=0;
j1=0; j2=0; j3=0; j4=0;
for i=1:num
if IDXO(i)==4
j4=j4+sqrt((p(i,1)-CO(1,1))^2+(p(i,2)-CO(1,2))^2+(p(i,3)-CO(1,3))^2);
end
end
JO=j1+j2+j3+j4;%四种类别的类内所有点与该类中心的距离和
JO
C=CO;J=JO;IDX=IDXO;
time=1;
Tbegin=10;Tover=0.1;%起始温度,终止温度
L=300; %内层循环次数,
T=Tbegin;%初始化温度参数
timeb=0;%最优目标首次出现的退火次数
% K=0.0001;
tic;
IDXN=IDXO;
while T>Tover
tt=0;
for inner=1:L
%产生随机扰动,即随机改变一个聚类样品的当前所属类别
t1=fix(rand*num+1); %随机抽取一个样本
t2=fix(rand*(centernum-1)+1); %随机生成1~3的整数
if(IDXN(t1)+t2>centernum)
IDXN(t1)=IDXN(t1)+t2-centernum;
else
IDXN(t1)=IDXN(t1)+t2;
end
% t1=fix(rand*(num-1)+1); %随机抽取一个样本
% t2=fix(rand*(centernum-1)+1); %随机生成1~4的整数
% if(IDXN(t1)+t2>centernum)
% IDXN(t1)=IDXN(t1)+t2-centernum;
% else
% IDXN(t1)=IDXN(t1)+t2;
% end
% IDXN(t1)=t2;
IDXN;
%重新计算聚类中心
p1=find(IDXN==1);%聚类号为1的样品在p中的序号
p11=p(p1,:);%全部为1类的样品矩阵
[b1, a1]=size(p1);
CN(1,:)=[sum(p11(:,1))/a1,sum(p11(:,2))/a1,sum(p11(:,3))/a1];%第一类的中心
p2=find(IDXN==2);%聚类号为2的样品在p中的序号
p22=p(p2,:);%全部为2类的样品矩阵
[b2, a2]=size(p2);
CN(2,:)=[sum(p22(:,1))/a2,sum(p22(:,2))/a2,sum(p22(:,3))/a2];%第2类的中心
p3=find(IDXN==3);%聚类号为3的样品在p中的序号
p33=p(p3,:);%全部为3类的样品矩阵
[b3, a3]=size(p3);
CN(3,:)=[sum(p33(:,1))/a3,sum(p33(:,2))/a3,sum(p33(:,3))/a3];%第3类的中心
p4=find(IDXN==4);%聚类号为1的样品在p中的序号
p44=p(p4,:);%全部为4类的样品矩阵
[b4, a4]=size(p4);
CN(4,:)=[sum(p44(:,1))/a4,sum(p44(:,2))/a4,sum(p44(:,3))/a4];%第4类的中心
%计算目标函数
JN=0;
j1=0; j2=0; j3=0; j4=0;
for i=1:num
if IDXN(i)==1
j1=j1+sqrt((p(i,1)-CN(1,1))^2+(p(i,2)-CN(1,2))^2+(p(i,3)-CN(1,3))^2);
elseif IDXN(i)==2
j2=j2+sqrt((p(i,1)-CN(2,1))^2 +(p(i,2)-CN(2,2))^2+(p(i,3)-CN(2,3))^2);
elseif IDXN(i)==3
j3=j3+sqrt((p(i,1)-CN(3,1))^2+(p(i,2)-CN(3,2))^2+(p(i,3)-CN(3,3))^2);
elseif IDXN(i)==4
j4=j4+sqrt((p(i,1)-CN(4,1))^2+(p(i,2)-CN(4,2))^2+(p(i,3)-CN(4,3))^2);
end
end
JN=j1+j2+j3+j4;%四种类别的类内所有点与该类中心的距离和
e=JN-JO;
%判断是否接受新解
if e<=0
JO=JN;CO=CN;IDXO=IDXN;
else
% if(rand<exp(-e/T))
% JO=JN;
% CO=CN;
% IDXO=IDXN;
% else
% IDXN=IDXO;IDX=IDXO;CN=CO;JN=JO;
% end
% end
% else
IDXN=IDXO;IDX=IDXO;CN=CO;
JN=JO;
end
end
%内层循环结束
T=T*0.9;
% if(T==0)
% break;
% end
time=time+1;
% if(time-timeb>1000)
% break;
% end
disp('已退火次数');
A=time-1
disp('最优目标函数值');
J=JO
end
time1=toc%退火需要的时间
hold on;
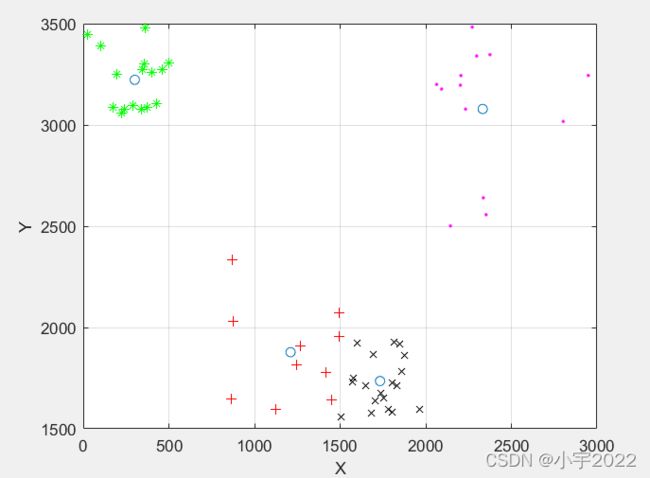
plot3(CO(:,1),CO(:,2),CO(:,3),'o');grid;box
%title('蚁群聚类结果(R=100,t=10000)')
xlabel('X')
ylabel('Y')
zlabel('Z')
index1 = find(IDXN == 1)
index2 = find(IDXN == 2)
index3 = find(IDXN == 3)
index4 = find(IDXN == 4)
plot3(p(index1,1),p(index1,2),p(index1,3),'r+');grid;
plot3(p(index2,1),p(index2,2),p(index2,3),'g*');grid;
plot3(p(index3,1),p(index3,2),p(index3,3),'kx');grid;
plot3(p(index4,1),p(index4,2),p(index4,3),'m.');grid;
>> moni
JO =
7.6551e+04
已退火次数
A =
1
最优目标函数值
J =
3.2015e+04
已退火次数
A =
2
最优目标函数值
J =
2.1396e+04
已退火次数
A =
3
最优目标函数值
J =
2.1396e+04
已退火次数
A =
4
最优目标函数值
J =
2.1396e+04
已退火次数
A =
5
最优目标函数值
J =
2.1396e+04
已退火次数
A =
6
最优目标函数值
J =
2.1396e+04
已退火次数
A =
7
最优目标函数值
J =
2.1396e+04
已退火次数
A =
8
最优目标函数值
J =
2.1396e+04
已退火次数
A =
9
最优目标函数值
J =
2.1396e+04
已退火次数
A =
10
最优目标函数值
J =
2.1396e+04
已退火次数
A =
11
最优目标函数值
J =
2.1396e+04
已退火次数
A =
12
最优目标函数值
J =
2.1396e+04
已退火次数
A =
13
最优目标函数值
J =
2.1396e+04
已退火次数
A =
14
最优目标函数值
J =
2.1396e+04
已退火次数
A =
15
最优目标函数值
J =
2.1396e+04
已退火次数
A =
16
最优目标函数值
J =
2.1396e+04
已退火次数
A =
17
最优目标函数值
J =
2.1396e+04
已退火次数
A =
18
最优目标函数值
J =
2.1396e+04
已退火次数
A =
19
最优目标函数值
J =
2.1396e+04
已退火次数
A =
20
最优目标函数值
J =
2.1396e+04
已退火次数
A =
21
最优目标函数值
J =
2.1396e+04
已退火次数
A =
22
最优目标函数值
J =
2.1396e+04
已退火次数
A =
23
最优目标函数值
J =
2.1396e+04
已退火次数
A =
24
最优目标函数值
J =
2.1396e+04
已退火次数
A =
25
最优目标函数值
J =
2.1396e+04
已退火次数
A =
26
最优目标函数值
J =
2.1396e+04
已退火次数
A =
27
最优目标函数值
J =
2.1396e+04
已退火次数
A =
28
最优目标函数值
J =
2.1396e+04
已退火次数
A =
29
最优目标函数值
J =
2.1396e+04
已退火次数
A =
30
最优目标函数值
J =
2.1396e+04
已退火次数
A =
31
最优目标函数值
J =
2.1396e+04
已退火次数
A =
32
最优目标函数值
J =
2.1396e+04
已退火次数
A =
33
最优目标函数值
J =
2.1396e+04
已退火次数
A =
34
最优目标函数值
J =
2.1396e+04
已退火次数
A =
35
最优目标函数值
J =
2.1396e+04
已退火次数
A =
36
最优目标函数值
J =
2.1396e+04
已退火次数
A =
37
最优目标函数值
J =
2.1396e+04
已退火次数
A =
38
最优目标函数值
J =
2.1396e+04
已退火次数
A =
39
最优目标函数值
J =
2.1396e+04
已退火次数
A =
40
最优目标函数值
J =
2.1396e+04
已退火次数
A =
41
最优目标函数值
J =
2.1396e+04
已退火次数
A =
42
最优目标函数值
J =
2.1396e+04
已退火次数
A =
43
最优目标函数值
J =
2.1396e+04
已退火次数
A =
44
最优目标函数值
J =
2.1396e+04
time1 =
0.6698
index1 =
8 14 15 18 19 22 24 35 36 43 45 49 50
index2 =
2 5 9 10 12 13 23 27 28 29 34 38 44 46 48 55
index3 =
列 1 至 19
1 3 7 11 17 20 21 26 30 31 33 37 40 41 47 51 52 57 58
列 20
59
index4 =
4 6 16 25 32 39 42 53 54 56
