NeRF神经辐射场学习笔记(十)— BungeeNeRF(CityNeRF)实现以及代码注释
NeRF神经辐射场学习笔记(十)— BungeeNeRF(CityNeRF)实现以及代码注释
- 声明
- 准备工作
- 运行测试
- 代码解读
-
- train()主体框架:
- BungeeNeRF代码改进概述:
- 1. 尺度界定——cur_stage:
- 2. BungeeNeRF网络构建——create_nerf()
-
- 2.1 Bungee_NeRF_block()类定义:
- 2.2 IPE位置编码——get_mip_embedder()
- 3. 对于光线的批量处理
- 4. 体素渲染——render()
-
- 4.1 基于圆锥体的采样
- 4.2 场景状态参数
- 参考文献和资料
声明
本人书写本系列博客目的是为了记录我学习三维重建领域相关知识的过程和心得,不涉及任何商业意图,欢迎互相交流,批评指正。
准备工作
首先从BungeeNeRF官网下载BungeeNeRF代码:
git clone https://github.com/city-super/BungeeNeRF.git
cd BungeeNeRF
创建anaconda环境并激活,
conda create --name <env_name> python=3.7
conda activate <env_name>
安装依赖库:
conda install pip; pip install --upgrade pip
pip install -r requirements.txt
创建data文件夹并下载数据集:
mkdir data
可以采用两种方式从Google Drive中获取数据集,本次实现主要基于第一种数据集来实现:
- 将 multiscale_google_56Leonard.zip 和 multiscale_google_Transamerica.zip 解压缩到数据data目录。 这两个文件夹包含渲染图像images和处理后的相机位姿poses_enu.json;
- 官网还提供了两个可以加载到Google Earth Studio中的.eps文件,可以调整相机轨迹并渲染最新的视图,城市的外观总是在GES中更新; 官网建议阅读相关操作指南来了解相机配置和允许的用途。
运行测试
代码默认尺度cur_stage从0开始,EXP_CONFIG_FILE是对应数据集的实验配置文件(56Leonard.txt或Transamerica.txt):
python run_bungee.py --config configs/EXP_CONFIG_FILE
若出现如下报错,参考教程进行更改:![]()
在run_bungee.py的第134行添加相应语句即可:
optimizer.param_groups[0]['capturable'] = True
python run_bungee.py --config configs/EXP_CONFIG_FILE --render_test
程序会识别最新一次的训练权重文件进行测试,例如cur_stage=0时的渲染结果为:

由于cur_stage=0,只提取了尺度为0的训练数据进行渲染,在精度以及数量上都无法达到最佳:
经过上一个尺度的训练后,可以通过指定cur_stage=1~3切换到下一个训练阶段,这将在训练集中包含一个更精细的尺度;并使用–ft_path指定的前一个阶段检查点开始训练,PREV_CKPT_PATH即为上一阶段保存的模型权重路径,例如./logs/56leonard_test_st0/200000.tar:
python run_bungee.py --config configs/EXP_CONFIG_FILE --cur_stage 1 --ft_path PREV_CKPT_PATH
cur_stage=1的渲染结果为:
cur_stage=1的渲染结果为:
最后的效果图为:
代码解读
BungeeNeRF代码是基于NeRF-pytorch-master进行开发的,该版本NeRF的代码讲解可以参考博主的另一篇博客NeRF神经辐射场学习笔记(二)——Pytorch版NeRF实现以及代码注释,所以本文仅对BungeeNeRF的改进部分做注释以及解读:
train()主体框架:
def train():
# 1.参数设置
parser = config_parser()
args = parser.parse_args()
# 2.输入数据和位姿,并处理数据、划分数据集,cur_stage:当前训练阶段,值越小,尺度越远,从0开始;
images, poses, scene_scaling_factor, scene_origin, scale_split = load_multiscale_data(args.datadir, args.factor)
...
images = images[scale_split[args.cur_stage]:]
poses = poses[scale_split[args.cur_stage]:]
...
...
# 3.初始化NeRF网络baseNeRF和resNeRF,返回render渲染训练和测试的相关信息,grad_var(整个网络的梯度变量)、optimizer(整个网络的优化器参数),其中包括IPE以及PE位置编码的实现;
render_kwargs_train, render_kwargs_test, start_iter, total_iter, grad_vars, optimizer = create_nerf(args)
...
...
# 4.生成光线后进行批量处理:
if args.use_batching:
rays = np.stack([get_rays_np(H, W, focal, p) for p in poses], 0)
...
# 5.训练主体:首先批量采样,每次从所有ray中抽取N_rand个ray,每遍历一边就打乱顺序(shuffle)
for i in trange(start_iter+1, args.N_iters+1):
if args.use_batching:
batch = torch.tensor(rays_rgb[i_batch : i_batch+args.N_rand]).to(device)
batch_radii = torch.tensor(radii[i_batch : i_batch+args.N_rand]).to(device)
batch_scale_codes = torch.tensor(scale_codes[i_batch : i_batch+args.N_rand]).to(device)
...
...
# 6.体素渲染的核心部分,渲染得到每个像素点的颜色信息,其中包括Mip-NeRF基于圆锥体cast的实现;
for stage in range(max(batch_scale_codes)+1):
rgb, _, _, _, extras = render(H, W, focal, batch_radii, chunk=args.chunk, rays=batch_rays, stage=stage, **render_kwargs_train)
...
...
...
global_step += 1
total_iter += 1
BungeeNeRF代码改进概述:
1. 尺度界定——cur_stage:
在BungeeNeRF代码中,要通过对cur_stage变量的设置来控制以下几件事情:
- 训练和测试数据集的划分:数据集按照四种由远到近的尺度进行排列保存,通过cur_stage对scale_split(数据集尺度索引list)的切片操作来实现数据集尺度的划分;
images, poses, scene_scaling_factor, scene_origin, scale_split = load_multiscale_data(args.datadir, args.factor)
...
images = images[scale_split[args.cur_stage]:] # cur_stage:当前训练阶段,值越小,尺度越远,从0开始;
poses = poses[scale_split[args.cur_stage]:]
- BungeeNeRF网络结构的创建: cur_stage的值会影响BungeeNeRF网络中resblock网络的数量,尺度越近,resblock数量越多,当cur_stage=0时,只有baseblock无resblock;下图为cur_stage=1时的BungeeNeRF网络结构:
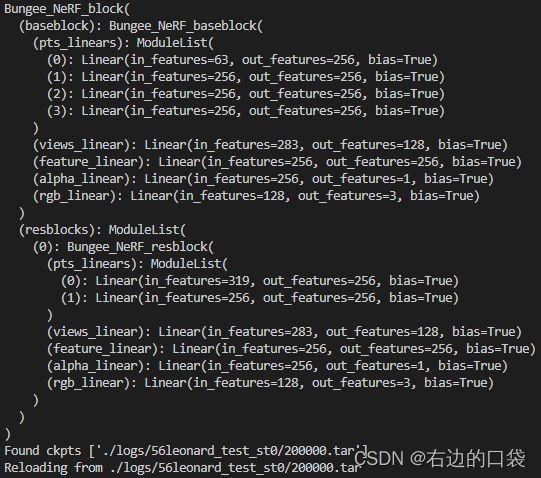
- 按照cur_stage尺度生成按尺度编码的图像矩阵,并且用来批量处理光线:
# 按照cur_stage尺度生成按尺度编码的图像矩阵,并且用来批量处理光线;
for spl in scale_split[:args.cur_stage+1]:
scale_codes.append(np.tile(np.ones(((prev_spl-spl),1,1,1))*cur_scale, (1,H,W,1))) # np.tile(numpy, (a,b))将原矩阵横向、纵向地复制b、a次,得到shape为(prev_spl-spl, H, W, 1)的矩阵;
prev_spl = spl
cur_scale += 1
scale_codes = np.concatenate(scale_codes, 0)
scale_codes = scale_codes.astype(np.int64)
2. BungeeNeRF网络构建——create_nerf()
初始化NeRF网络baseNeRF和resNeRF,返回render渲染训练和测试的相关信息,grad_var(整个网络的梯度变量)、optimizer(整个网络的优化器参数);
start_iter是开始的迭代次数,初始值为零,若stage>0,则寻找已训练模型的路径并加载,赋值为ckpt[‘global_step’],total_iter = ckpt[‘total_iter’];
render_kwargs_train和render_kwargs_test为两个字典型变量,里面存储着渲染场景时所需数据;
‘network_query_fn’ : network_query_fn,一个匿名函数,给这个函数输入位置坐标,方向坐标,以及神经网络,就可以利用神经网络返回该点对应的颜色和密度;
2.1 Bungee_NeRF_block()类定义:
class Bungee_NeRF_block(nn.Module):
def __init__(self, num_resblocks=3, net_width=256, input_ch=3, input_ch_views=3):
super(Bungee_NeRF_block, self).__init__()
self.input_ch = input_ch
self.input_ch_views = input_ch_views
self.num_resblocks = num_resblocks
self.baseblock = Bungee_NeRF_baseblock(net_width=net_width, input_ch=input_ch, input_ch_views=input_ch_views)
self.resblocks = nn.ModuleList([
Bungee_NeRF_resblock(net_width=net_width, input_ch=input_ch, input_ch_views=input_ch_views) for _ in range(num_resblocks)
])
def forward(self, x):
... # 前向传播函数,输出预测图像颜色;
return output
其中包括了baseblock和resblock的定义,对应的网络结构图如下所示:
class Bungee_NeRF_baseblock(nn.Module):
def __init__(self, net_width=256, input_ch=3, input_ch_views=3):
super(Bungee_NeRF_baseblock, self).__init__()
self.pts_linears = nn.ModuleList([nn.Linear(input_ch, net_width)] + [nn.Linear(net_width, net_width) for _ in range(3)])
self.views_linear = nn.Linear(input_ch_views + net_width, net_width//2)
self.feature_linear = nn.Linear(net_width, net_width)
self.alpha_linear = nn.Linear(net_width, 1)
self.rgb_linear = nn.Linear(net_width//2, 3)
def forward(self, input_pts, input_views):
...
return rgb, alpha, h
return rgb, alpha, h
class Bungee_NeRF_resblock(nn.Module):
def __init__(self, net_width=256, input_ch=3, input_ch_views=3):
super(Bungee_NeRF_resblock, self).__init__()
self.pts_linears = nn.ModuleList([nn.Linear(input_ch+net_width, net_width), nn.Linear(net_width, net_width)])
self.views_linear = nn.Linear(input_ch_views + net_width, net_width//2)
self.feature_linear = nn.Linear(net_width, net_width)
self.alpha_linear = nn.Linear(net_width, 1)
self.rgb_linear = nn.Linear(net_width//2, 3)
def forward(self, input_pts, input_views, h):
...
2.2 IPE位置编码——get_mip_embedder()
get_mip_embedder函数:
def get_mip_embedder(multires, min_multires=0, i=0, include_input=True, log_sampling=True):
if i == -1:
return nn.Identity(), 3
embed_kwargs = {
'include_input' : include_input,
'input_dims' : 3,
'min_freq_log2': min_multires,
'max_freq_log2' : multires-1,
'num_freqs' : multires,
'log_sampling' : log_sampling,
'periodic_fns' : [torch.sin, torch.cos],
}
embedder_obj = MipEmbedder(**embed_kwargs)
embed = lambda inputs, eo=embedder_obj : eo.embed(inputs)
return embed, embedder_obj.out_dim
MipEmbedder类定义:
class MipEmbedder:
def __init__(self, **kwargs):
self.kwargs = kwargs
self.create_embedding_fn()
def create_embedding_fn(self):
embed_fns = []
d = self.kwargs['input_dims']
out_dim = 0
if self.kwargs['include_input']:
embed_fns.append(lambda x : x[:,:d])
out_dim += d
max_freq = self.kwargs['max_freq_log2']
min_freq = self.kwargs['min_freq_log2']
N_freqs = self.kwargs['num_freqs']
if self.kwargs['log_sampling']:
freq_bands_y = 2.**torch.linspace(min_freq, max_freq, steps=N_freqs)
freq_bands_w = 4.**torch.linspace(min_freq, max_freq, steps=N_freqs)
else:
freq_bands_y = torch.linspace(2.**min_freq, 2.**max_freq, steps=N_freqs)
freq_bands_w = torch.linspace(4.**min_freq, 4.**max_freq, steps=N_freqs)
for ctr in range(len(freq_bands_y)):
for p_fn in self.kwargs['periodic_fns']:
embed_fns.append(lambda inputs, p_fn=p_fn, freq_y=freq_bands_y[ctr], freq_w=freq_bands_w[ctr] : p_fn(inputs[:,:d] * freq_y) * torch.exp((-0.5) * freq_w * inputs[:,d:]))
out_dim += d
self.embed_fns = embed_fns
self.out_dim = out_dim
def embed(self, inputs):
return torch.cat([fn(inputs) for fn in self.embed_fns], -1)
集成位置编码实现:(代码中这一部分没有调用,但是对其进行了声明,可以修改MipEmbedder中的create_embedding_fn进行调用)
def integrated_pos_enc(x_coord, min_freq, max_freq, N_freqs):
x, x_cov_diag = x_coord[:,:3], x_coord[:,3:]
scales = 2.**torch.linspace(min_freq, max_freq, steps=N_freqs)
shape = list(x.shape[:-1]) + [-1]
y = torch.reshape(x[..., None, :] * scales[:, None], shape)
y_var = torch.reshape(x_cov_diag[..., None, :] * scales[:, None]**2, shape)
embedding = expected_sin(
torch.cat([y, y + 0.5 * math.pi], axis=-1),
torch.cat([y_var] * 2, axis=-1))[0]
return embedding
def expected_sin(x, x_var):
y = torch.exp(-0.5 * x_var) * torch.sin(x)
y_var = torch.maximum(
torch.tensor(0), 0.5 * (1 - torch.exp(-2 * x_var) * torch.cos(2 * x)) - y**2)
return y, y_var
3. 对于光线的批量处理
首先按照尺度编码生成scale_codes矩阵,该矩阵按原数据集尺度顺序排列,矩阵中的数值表示该图像所属的尺度:
scale_codes = []
prev_spl = n_images # 463(56Leonard)
cur_scale = 0
# 按照cur_stage尺度生成图像尺度编码矩阵scale_codes,并且用来批量处理光线;
# cur_stage=0时,scale_split[:args.cur_stage+1]=[275],cur_stage=1时,scale_split[:args.cur_stage+1]=[275,150],以此类推;
for spl in scale_split[:args.cur_stage+1]:
scale_codes.append(np.tile(np.ones(((prev_spl-spl),1,1,1))*cur_scale, (1,H,W,1))) # np.tile(numpy, (a,b))将原矩阵横向、纵向地复制b、a次,得到shape为(prev_spl-spl, H, W, 1)的矩阵;
'''
np.ones(((prev_spl-spl),1,1,1))是(188,1,1,1)shape的全1矩阵,[[[[1.]]],...,[[[1.]]]];
乘上cur_scale后为全0矩阵,紧接着np.tile(np.ones(((prev_spl-spl),1,1,1))*cur_scale, (1,H,W,1))在第2、3维度进行扩展,扩展为shape(188,360,640,1),放入scale_codes中;
若cur_stage大于0的话,scale_codes就是一个保存多个尺度图像数据矩阵的list,其中第1维度代表该尺度的图像数量、第2、3维度表示图像大小、矩阵中的数值代表着cur_stage阶段;
'''
prev_spl = spl
cur_scale += 1
scale_codes = np.concatenate(scale_codes, 0) # 然后将scale_codes按0维合并,即按尺度顺序合并为shape(stage_image_num,H,W,1)
scale_codes = scale_codes.astype(np.int64)
紧接着生成光线数据用于渲染,并合并打乱:
if args.use_batching:
rays = np.stack([get_rays_np(H, W, focal, p) for p in poses], 0)
# get_rays返回rays_o, rays_d,directions即取出rays_d(生成的光线方向,shape(188,H,W,3)),rays_o为188*H*W的[-1.69913279, 3.0930094 , 4.12601929]
directions = rays[:,1,:,:,:]
dx = np.sqrt(
np.sum((directions[:, :-1, :, :] - directions[:, 1:, :, :])**2, -1)) # 前一张图片的rays_d-后一张图片的rays_d,取平方,再按照最后一个维度求和再取平方根,得到shape为(188,H-1,W),即求向量距离;
dx = np.concatenate([dx, dx[:, -2:-1, :]], 1) # 再将最后一个rays_d补齐shape为(188,H,W),dx代表着同一像素点相邻图片的生成光线向量的距离大小;
radii = dx[..., None] * 2 / np.sqrt(12) # dx[..., None]将dx扩充一个维度(188,H,W,1),弥补sum缺失的维度,然后*2再除以根号12
rays_rgb = np.concatenate([rays, images[:,None]], 1) # 合并光线与图像shape为(188,3,H,W,3)
rays_rgb = np.transpose(rays_rgb, [0,2,3,1,4]) # 变换坐标轴(188,H,W,3,3),之后取训练集
rays_rgb = np.stack([rays_rgb[i] for i in i_train], 0)
radii = np.stack([radii[i] for i in i_train], 0)
scale_codes = np.stack([scale_codes[i] for i in i_train], 0)
# 将数组维度改变为(train_num*H*W,3,3),3*3的数据对应着每一张图片中的每一个像素点的颜色、rays_d和rays_o
rays_rgb = np.reshape(rays_rgb, [-1,3,3])
radii = np.reshape(radii, [-1, 1])
scale_codes = np.reshape(scale_codes, [-1, 1])
print('shuffle rays') # 打乱光线,重新分布
rand_idx = torch.randperm(rays_rgb.shape[0])
rays_rgb = rays_rgb[rand_idx.cpu().data.numpy()]
radii = radii[rand_idx.cpu().data.numpy()]
scale_codes = scale_codes[rand_idx.cpu().data.numpy()]
print('done')
i_batch = 0
在训练过程中,每次批量处理N_banch个光线数据,从rays_rgb中取出,取出的数量超过rays_rgb数量后,再次打乱数据:
for i in trange(start_iter+1, args.N_iters+1):
if args.use_batching:
batch = torch.tensor(rays_rgb[i_batch : i_batch+args.N_rand]).to(device)
batch_radii = torch.tensor(radii[i_batch : i_batch+args.N_rand]).to(device)
batch_scale_codes = torch.tensor(scale_codes[i_batch : i_batch+args.N_rand]).to(device)
batch = torch.transpose(batch, 0, 1)
batch_rays, target_s = batch[:2], batch[2]
i_batch += args.N_rand
if i_batch >= rays_rgb.shape[0]:
print("Shuffle data after an epoch!")
rand_idx = torch.randperm(rays_rgb.shape[0])
rays_rgb = rays_rgb[rand_idx.cpu().data.numpy()]
radii = radii[rand_idx.cpu().data.numpy()]
scale_codes = scale_codes[rand_idx.cpu().data.numpy()]
i_batch = 0
4. 体素渲染——render()
4.1 基于圆锥体的采样
该部分代码的原理是按照Mip-NeRF中基于圆锥体的像素点采样去做的,具体公式和推导可以参考博主的另一篇博客NeRF神经辐射场学习笔记(四)——Mip NeRF论文创新点解读,主要公式如下:
针对基于圆锥体采样方式,原始的位置编码表达式的积分没有封闭形式的解,不能有效地计算。故文章采用了一个多元高斯函数(multivariate Gaussian)来近似圆锥截面,这可以有效地近似成所需要的特征(allows for an efficient approximation to the desired feature)。为了用多元高斯函数逼近圆锥台,我们必须计算 F ( x , ⋅ ) F(\textbf{x},\cdot) F(x,⋅)的均值和协方差,因为每个圆锥台假定是圆形的,而且圆锥台绕锥体的轴线是对称的,所以除了 o \textbf{o} o和 d \textbf{d} d以外,这种高斯模型完全由3个值来表示: μ t \mu_t μt(沿射线的平均距离)、 σ t 2 \sigma^2_t σt2(沿射线方向的方差)、 σ r 2 \sigma^2_r σr2(沿射线垂直方向的方差): μ t = t μ + 2 t μ t δ 2 3 t μ 2 + t δ 2 , σ t 2 = t t 2 3 − 4 t δ 4 ( 12 t μ 2 − t δ 2 ) 15 ( 3 t μ 2 + t δ 2 ) 2 , σ r 2 = r ˙ 2 ( t μ 2 4 + 5 t δ 2 12 − 4 t δ 4 15 ( 3 t μ 2 + t δ 2 ) ) \mu_t=t_{\mu}+\frac{2t_{\mu}t^2_{\delta}}{3t^2_{\mu}+t^2_{\delta}}, \sigma^2_t=\frac{t^2_t}{3}-\frac{4t^4_{\delta}(12t^2_{\mu}-t^2_{\delta})}{15(3t^2_{\mu}+t^2_{\delta})^2}, \sigma^2_r=\dot{r}^2\left(\frac{t^2_{\mu}}{4}+\frac{5t^2_{\delta}}{12}-\frac{4t^4_{\delta}}{15(3t^2_{\mu}+t^2_{\delta})}\right) μt=tμ+3tμ2+tδ22tμtδ2,σt2=3tt2−15(3tμ2+tδ2)24tδ4(12tμ2−tδ2),σr2=r˙2(4tμ2+125tδ2−15(3tμ2+tδ2)4tδ4)其中定义中点为 t μ = ( t 0 + t 1 ) t_{\mu}=(t_0+t_1) tμ=(t0+t1),半宽为 t δ = ( t 1 − t 0 ) / 2 t_{\delta}=(t_1-t_0)/2 tδ=(t1−t0)/2,上述变量都是根据这两个参数定义的,并且对数值稳定性至关重要。
紧接着可以将这个高斯模型从圆锥台的坐标系转换成世界坐标,得到最终的多元高斯模型: μ = o + μ t d , Σ = σ t 2 ( d d T ) + σ r 2 ( I − d d T ∣ ∣ d ∣ ∣ 2 2 ) \mu=\textbf{o}+\mu_t\textbf{d}, \Sigma=\sigma^2_t(\textbf{d}\textbf{d}^T)+\sigma^2_r\left(\textbf{I}-\frac{\textbf{d}\textbf{d}^T}{||\textbf{d}||^2_2}\right) μ=o+μtd,Σ=σt2(ddT)+σr2(I−∣∣d∣∣22ddT)
def cast(origin, direction, radius, t):
t0, t1 = t[..., :-1], t[..., 1:]
c, d = (t0 + t1)/2, (t1 - t0)/2
t_mean = c + (2*c*d**2) / (3*c**2 + d**2)
t_var = (d**2)/3 - (4/15) * ((d**4 * (12*c**2 - d**2)) / (3*c**2 + d**2)**2)
r_var = radius**2 * ((c**2)/4 + (5/12) * d**2 - (4/15) * (d**4) / (3*c**2 + d**2))
mean = origin[...,None,:] + direction[..., None, :] * t_mean[..., None]
null_outer_diag = 1 - (direction**2) / torch.sum(direction**2, -1, keepdims=True)
cov_diag = (t_var[..., None] * (direction**2)[..., None, :] + r_var[..., None] * null_outer_diag[..., None, :])
return mean, cov_diag
4.2 场景状态参数
- ray_nearfar:地球的表示方式,sphere还是plane;
if ray_nearfar == 'sphere': ## 将地球视为球体并计算射线与球体的交点
globe_center = torch.tensor(np.array(scene_origin) * scene_scaling_factor).float()
# 6371011 是地球半径,250是场景中建筑物的假设高度限制
earth_radius = 6371011 * scene_scaling_factor
earth_radius_plus_bldg = (6371011+250) * scene_scaling_factor
## 与建筑上限球体的交点
delta = (2*torch.sum((rays_o-globe_center) * rays_d, dim=-1))**2 - 4*torch.norm(rays_d, dim=-1)**2 * (torch.norm((rays_o-globe_center), dim=-1)**2 - (earth_radius_plus_bldg)**2)
d_near = (-2*torch.sum((rays_o-globe_center) * rays_d, dim=-1) - delta**0.5) / (2*torch.norm(rays_d, dim=-1)**2)
rays_start = rays_o + (d_near[...,None]*rays_d)
## 与地球的交点
delta = (2*torch.sum((rays_o-globe_center) * rays_d, dim=-1))**2 - 4*torch.norm(rays_d, dim=-1)**2 * (torch.norm((rays_o-globe_center), dim=-1)**2 - (earth_radius)**2)
d_far = (-2*torch.sum((rays_o-globe_center) * rays_d, dim=-1) - delta**0.5) / (2*torch.norm(rays_d, dim=-1)**2)
rays_end = rays_o + (d_far[...,None]*rays_d)
## 计算每条光线的距离范围
new_near = torch.norm(rays_o - rays_start, dim=-1, keepdim=True)
near = new_near * 0.9
new_far = torch.norm(rays_o - rays_end, dim=-1, keepdim=True)
far = new_far * 1.1
# 前半部分的视差采样和其余部分的线性采样
t_vals_lindisp = torch.linspace(0., 1., steps=N_samples)
z_vals_lindisp = 1./(1./near * (1.-t_vals_lindisp) + 1./far * (t_vals_lindisp))
z_vals_lindisp_half = z_vals_lindisp[:,:int(N_samples*2/3)]
linear_start = z_vals_lindisp_half[:,-1:]
t_vals_linear = torch.linspace(0., 1., steps=N_samples-int(N_samples*2/3)+1)
z_vals_linear_half = linear_start * (1-t_vals_linear) + far * t_vals_linear
z_vals = torch.cat((z_vals_lindisp_half, z_vals_linear_half[:,1:]), -1)
z_vals, _ = torch.sort(z_vals, -1)
z_vals = z_vals.expand([N_rays, N_samples])
- scene_scaling_factor:场景相对于地球真实距离的比例尺系数;
- scene_origin:场景相机拍摄时的原点;
参考文献和资料
[1]BungeeNeRF原文
[2]BungeeNeRF官网
[3]BungeeNeRF代码