【定量分析、量化金融与统计学】R语言方差分析ANOVA(F检验)
目录
一、前言
Fixed-effects models、Random-effects models、Mixed-effects models。
二、ANOVA使用的前提假设与假设检验
三、ANOVA的计算原理
四、事后检验与交叉图:
五、R语言进行分析的完整例子:
六、结果
一、前言
今天来说一说概率论或者统计学中常用的一种检验方式,方差检验ANOVA.
根据定义:方差分析(ANOVA)是一组统计模型及其相关估计程序的集合。
方差分析基于总方差的规律,其中观察到的某一特定变量的方差被划分为可归因于不同来源的变异的成分。在其最简单的形式,方差分析提供了两个或多个总体均值是否相等的统计检验,因此扩大了超过两个均值的t检验。换句话说,方差分析是用来测试两个或多个平均值之间的差异。
ANOVA的模型有很多:
Fixed-effects models、Random-effects models、Mixed-effects models。
但是今天我们不说那么细。
直说基本的ANOVA,one-way的与two-way的,并写一个基础的R语言demo。
二、ANOVA使用的前提假设与假设检验
下面是ANOVA的假设前提:
- 观察的独立性——这是简化统计分析的模型的一个假设。
- 正态性,残差分布是正态的。
- 方差相等(或“同质”),称为同方差——组内数据的方差应该相同。
所以在进行ANOVA之前你要对以上的假设进行检验,我们的样本符合这样的要求么?
独立性问题我们没有程序的办法进行检验,但是正态性与齐次性我们是必须检验的。
- 常见的正态检验:SW test用于较小的数据集,KS test用于大数据集的检验。
- 齐次性检验:Levene's test,我们一般会有三种不同的Levene's test,(1)使用平均值(计算方差的标准方法)(2)使用中位数(用上面的中位数代替平均值)(3)使用10%修剪后的平均值(用上面10%修剪后的平均值代替平均值)。我们可以根据需求随意选择。
三、ANOVA的计算原理
当我们一切假设检验都完成之后,我们就开始ANOVA了。
那么ANOVA怎么计算呢?
我们首先明确,ANOVA只能有一个因变量,但是自变量的个数可以随意,如果只有一个自变量那就是one-way ANOVA,多个自变量就是two-way ANOVA。
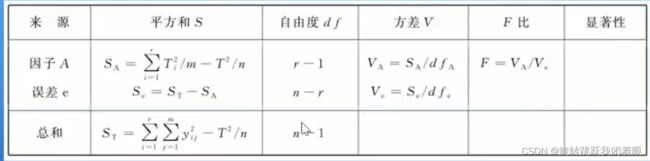
那么我们给一个单因素和多因素ANOVA分析的表格方法:
one-way:
two-way:
一般情况下我们是不手动计算的,因为很复杂,我们会使用SPSS,Eviews,R或者python等等工具帮助我们,所以详细的手动公式我就不展开了。
四、事后检验与交叉图:
最终我们会得到一个F比,那么ANOVA做完了,这个ANOVA效果怎么样,得到了准确的结果了么?
我们就需要事后检验。
我们常用:Turkey检验或者TamhaneT2Test
交叉图是two-way时,我们想看是否有交叉影响。
我们会在程序中看到什么是交叉图。
五、R语言进行分析的完整例子:
例子是:一家公司准备分析产品质量和用户类型的关系。
数据集经过脱敏处理:
1.读数据与正态检验
x=read.csv(file.choose(),header=TRUE)
# 首先进行假设检验
# 正态检验!
boxplot(x$x6)
# x6 is DV : product quality
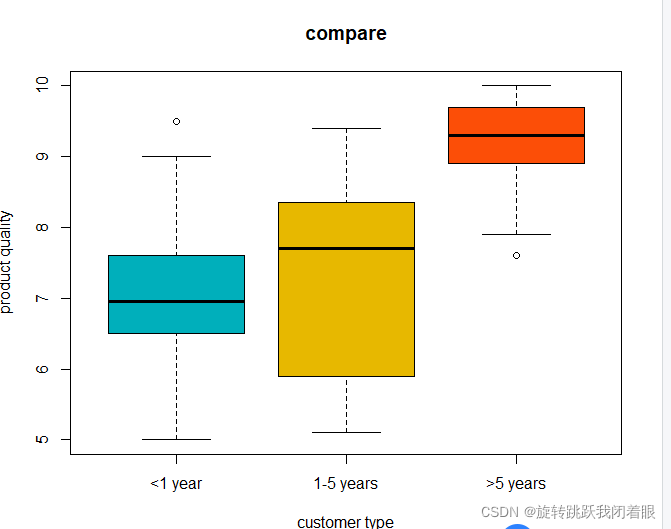
boxplot(x6 ~ x1, data = x,
xlab = "customer type", ylab = "product quality",
main = "compare", col = c("#00AFBB", "#E7B800", "#FC4E07")
, names=c("<1 year","1-5 years",">5 years") )
boxplot(x6 ~ x1, data = x,
xlab = "customer type", ylab = "product quality",
main = "compare", col = c("red", "blue", "green")
, names=c("<1 year","1-5 years",">5 years") )
hist(x$x6)
hist(x[x$x1==1, ]$x6)
hist(x[x$x1==2, ]$x6)
hist(x[x$x1==3, ]$x6)
#SW test
shapiro.test(x$x6)2.齐次性检验
install.packages("lawstat")
library("lawstat")
levene.test(x$x6,x$x1,location=c("mean"))
levene.test(x$x6,x$x1,location=c("median"))
levene.test(x$x6,x$x1,location=c("trim.mean"))3.one-way ANOVA
fit<-aov(x6~as.factor(x1),data=x)
summary(fit)4.事后检验
#Tamhane
summary(T2 <- tamhaneT2Test(x$x6, as.factor(x$x1):as.factor(x$x2)))然后就结束了。
在two-way中,需要交叉图:
#INTERACTION PLOT
install.packages("gplots")
library("gplots")
interaction.plot(as.factor(x$x1),as.factor(x$x2), x$x6,type="b", col=c(1:3),
leg.bty="o", leg.bg="beige", lwd=2, pch=c(18,24,22),
xlab="customer type",
ylab="estimated marginal means",
main="Interaction Plot")最后将结果变成报告就可以了。
六、结果
正态性:
齐次性:
ANOVA:
我们可以看到,是极其显著,有三颗星。
事后检验: