机器学习第三章 多变量线性回归
文章目录
- 第三章 多变量线性回归(Multivariate Linear Regression)
-
- 多变量梯度下降
-
- 梯度下降运算中的使用技巧
-
- 特征缩放(feature scaling)
- 定义新的特征
- 多项式回归
- 正规方程(normal equation)
-
- 梯度下降与正规方程的比较
- 后言
第三章 多变量线性回归(Multivariate Linear Regression)
多变量线性回归有多个特征值,所以在多变量线性回归里
n代表特征值的个数
x ( i ) x^{(i)} x(i)代表第i个训练样本的输入特征向量,是一个n维的列向量(在单变量线性回归中 x ( i ) x^{(i)} x(i)代表一个特征值)
x j ( i ) x^{(i)}_j xj(i)代表第i个训练样本中第j个特征量的值
假设函数: h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . θ n x n h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + ...\theta_nx_n hθ(x)=θ0+θ1x1+θ2x2+...θnxn
为了方便定义,将参数和特征值分别定义成一个向量,我们取 x 0 x_0 x0=1,所以 x = [ x 0 , x 1 , x 2 , . . . , x n ] T x= [x_0,x_1,x_2,...,x_n]^T x=[x0,x1,x2,...,xn]T, θ = [ θ 0 , θ 1 , θ 2 , . . . , θ n ] T \theta = [\theta_0,\theta_1,\theta_2,...,\theta_n]^T θ=[θ0,θ1,θ2,...,θn]T
从而得到假设函数: h θ ( x ) = θ T x h_\theta(x) = \theta^T x hθ(x)=θTx
代价函数:
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta) = \frac{1}{2m} \sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2 J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
多变量梯度下降
将代价函数带入到梯度下降公式里就得到了在多变量线性回归中应用梯度下降的算法
r e p e a d u n t i l c o n v e r g e n c e { θ 0 = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) θ 1 = θ 1 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 1 ( i ) θ 2 = θ 2 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 2 ( i ) . . . θ n = θ n − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x n ( i ) } repead \ \ until \ \ convergence\{\\ \theta_0=\theta_0-\alpha\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_0\\ \theta_1=\theta_1-\alpha\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_1\\ \theta_2=\theta_2-\alpha\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_2\\ ...\\ \theta_n=\theta_n-\alpha\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_n\\ \} repead until convergence{θ0=θ0−αm1i=1∑m(hθ(x(i))−y(i))x0(i)θ1=θ1−αm1i=1∑m(hθ(x(i))−y(i))x1(i)θ2=θ2−αm1i=1∑m(hθ(x(i))−y(i))x2(i)...θn=θn−αm1i=1∑m(hθ(x(i))−y(i))xn(i)}
即
r e p e a d u n t i l c o n v e r g e n c e { θ j = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) , j = 0 , 1 , 2 , . . . n } repead \ \ until \ \ convergence\{\\ \theta_j=\theta_j-\alpha\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_j,\ \ \ j = 0,1,2,...n\\ \} repead until convergence{θj=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i), j=0,1,2,...n}
注意这里参数 θ 0 \theta_0 θ0到 θ n \theta_n θn应该是同步更新的,可以用for循环逐个更新这些参数值,也可以使用向量化把n+1个参数同时更新
梯度下降运算中的使用技巧
特征缩放(feature scaling)
有的时候不同特征的取值范围差异很大,这样往往会导致机器学习算法的性能表现不佳,这个时候就需要保持特征处于相似的尺度上,这样做可以将梯度下降算法运行速度变得更快,使收敛所需要的迭代次数更少,加快收敛到全局最小值
均值归一化(mean normalization)
x i = x i − μ i s i x_i = \frac{x_i-\mu_i}{s_i} xi=sixi−μi
特征缩放有两种常用方法:
归一化:又叫做最小-最大缩放,将该值减去最小值并除以最大值与最小值的差,其中 μ i \mu_i μi为最小值, s i s_i si为 x i x_i xi中的最大值减去最小值,最终范围归于0~1之间
标准化:将该值减去平均值再除以方差,其中 μ i \mu_i μi为平均值, s i s_i si为标准差,标准化不将值绑定到某个范围
学习率 α \alpha α(learning rate)
为了检验梯度下降算法使朝着正确的方向进行,可以绘制代价函数与迭代次数之间的函数图
若代价函数随着其迭代次数增加而逐渐减小,最终收敛于某个值,则认为算法正常工作
若代价函数随着迭代次数的增加不降反增,或是一会升一会降,那么就要对算法做出修正,这两种情况的解决方法通常是减小 α \alpha α的值
这里右边这个图有错,横轴自变量应该是 θ \theta θ
只要学习率足够小,那么每次迭代之后代价函数 J ( θ ) J(\theta) J(θ)都会减小,但学习率太小,梯度下降算法可能收敛得很慢。所以应该选择一个合适的 α \alpha α值
为了选择合适的学习率 α \alpha α,吴恩达老师通常会取值 . . . ... ...,0.001,0.003,0.01,0.03,0.1,0.3,1, . . . ... ...,找到一个合适的最小值和最大值,若都满足则取最大值,或者稍微小一点的值
定义新的特征
以预测房屋价格为例,假设房屋价格有两个特征,一个是房屋占地的宽 x 1 x_1 x1,一个是房屋占地的长 x 2 x_2 x2,则假设函数为 h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 hθ(x)=θ0+θ1x1+θ2x2
若我们创造一个新的特征房屋的占地面积 x = x 1 ∗ x 2 x=x_1*x_2 x=x1∗x2,则可得到新的假设函数为 h θ ( x ) = θ 0 + θ 1 x h_\theta(x) = \theta_0 + \theta_1x hθ(x)=θ0+θ1x,通过定义新的特征,可能会得到一个更好的模型
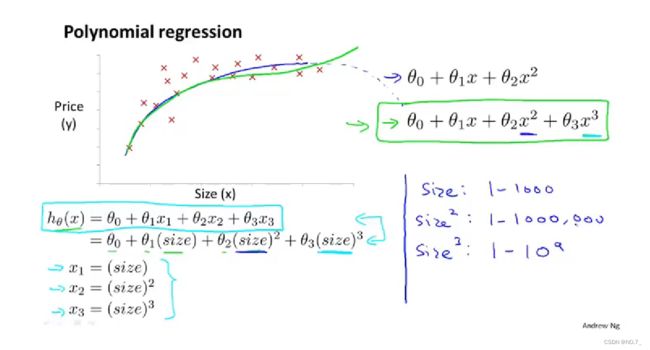
多项式回归
当特征值与预测值显然是非直线关系时,可以用多项式回归来拟合。多项式回归可以用线性回归的方法来拟合,非常复杂的函数,甚至是非线性函数都可以。将非线性回归转化成线性回归
例如我们可以将第一个特征 x 1 x_1 x1设为房屋占地面积,将第二个特征 x 2 x_2 x2设为房屋占地面积的平方,将第三个特征 x 3 x_3 x3设为房屋占地面积的立方,通过对这三个特征的这样设置,得到假设函数为 h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_3 hθ(x)=θ0+θ1x1+θ2x2+θ3x3,再通过线性回归的方法,就可以拟合这样的模型(三次函数)。如果像这样选择特征,特征缩放就十分重要了,因为这时三个特征的取值范围可能差别巨大
正规方程(normal equation)
正规方程是一种求 θ \theta θ的快速解法, 它是通过求解方程 ∂ ∂ θ J ( θ ) = 0 \frac{\partial}{\partial\theta}J(\theta)=0 ∂θ∂J(θ)=0来找出使得代价函数最小的参数的 θ \theta θ,不需要进行特征缩放,通过数学推导(详细推导过程省略)可解得 θ = ( X T X ) − 1 X T y \theta=(X^TX)^{-1}X^Ty θ=(XTX)−1XTy
x ( i ) = [ x 0 ( i ) x 1 ( i ) ⋮ x n ( i ) ] , X = [ 1 x 1 ( 1 ) ⋯ x j ( 1 ) ⋯ x n ( 1 ) 1 x 1 ( 2 ) ⋯ x j ( 2 ) ⋯ x n ( 2 ) ⋮ ⋮ ⋱ ⋮ ⋱ ⋮ 1 x 1 ( m ) ⋯ x j ( m ) ⋯ x n ( m ) ] = [ ( x ( 1 ) ) T ( x ( 2 ) ) T ⋮ ( x ( m ) ) T ] , y = x ( i ) = [ y ( 1 ) y ( 2 ) ⋮ y ( m ) ] x^{(i)} = \left[\begin{matrix} x_0^{(i)}\\ x_1^{(i)}\\ \vdots\\ x_n^{(i)} \end{matrix}\right] ,\ \ \ \ X=\left[\begin{matrix} 1 & x_1^{(1)} & \cdots & x_j^{(1)} & \cdots & x_n^{(1)}\\ 1 & x_1^{(2)} & \cdots & x_j^{(2)} & \cdots & x_n^{(2)}\\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots\\ 1 & x_1^{(m)} & \cdots & x_j^{(m)} & \cdots & x_n{(m)}\\ \end{matrix}\right] =\left[\begin{matrix} (x^{(1)})^T\\ (x^{(2)})^T\\ \vdots\\ (x^{(m)})^T \end{matrix}\right] ,\ \ \ \ \ y =x^{(i)} = \left[\begin{matrix} y^{(1)}\\ y^{(2)}\\ \vdots\\ y^{(m)} \end{matrix}\right] x(i)=⎣⎢⎢⎢⎢⎡x0(i)x1(i)⋮xn(i)⎦⎥⎥⎥⎥⎤, X=⎣⎢⎢⎢⎢⎡11⋮1x1(1)x1(2)⋮x1(m)⋯⋯⋱⋯xj(1)xj(2)⋮xj(m)⋯⋯⋱⋯xn(1)xn(2)⋮xn(m)⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎡(x(1))T(x(2))T⋮(x(m))T⎦⎥⎥⎥⎤, y=x(i)=⎣⎢⎢⎢⎡y(1)y(2)⋮y(m)⎦⎥⎥⎥⎤
X X X为所有输入特征值组成的矩阵, x 0 ( i ) x_0^{(i)} x0(i)不是特征,但我们令它为1,正规方程存在条件是 X T X X^TX XTX可逆
对于线性回归这个特定的模型,正规方程法是一个比梯度下降法更快的替代算法(在特征量不是特别大的情况下,NG认为特征量小于10000使用正规方程法更好)
梯度下降与正规方程的比较
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择 α \alpha α | 不需要选择 α \alpha α |
| 需要进行多次迭代 | 只需要一次计算 |
| 当特征数量n大时也能较好适用 | 需要计算 ( X T X ) − 1 (X^TX)^{-1} (XTX)−1当特征数量n大时会很慢 |
| 适应于各种类型的模型 | 只适用于线性模型,不适合Logisic回归等其他模型 |
后言
至此,线性回归告一段落。