机器学习：Experiment 2: Multivariate Linear Regression

实验目的

根据给出的例子和数据，实现梯度下降和正规方程的多元线性回归算法，可以使用 matlab （或者 octave）进行实现。 检查损失函数 J(θ)、梯度下降的收敛性和学习率α之间的关系并最终将结果展示出来。

软件环境

MATLAB Octave

实验步骤与内容：

1. 数据加载

这是俄勒冈州波特兰市的房价训练集，输出 y(i)是价格，输入 x(i)是居住面积和卧室数。 有 m = 47 个训练例子

x = load('ex2x.dat'); 
y = load('ex2y.dat');

2.数据预处理

a.将训练示例的数据加载到程序中，并将$x_0=1$ 的截距项添加到 x 矩阵中。回想一下 Matlab/Octave 中用于添加一列 1 的命令是

x=[ones(m,1),x];%add one column

b.看一下输入 x(i)的值，注意到客厅面积大约是卧室数量的 1000 倍。这一差异意味着对输 入进行预处理将显著提高梯度下降的效率。在您的程序中，将这两种类型的输入按其标准差 进行缩放，并将其均值设置为零。在 Matlab/Octave，这可以执行

sigma=std(x);%standard deviation 
mu=mean(x);%average value 
x(:,2)=(x(:,2)-mu(2))./sigma(2); %compute 
x(:,3)=(x(:,3)-mu(3))./sigma(3);

c.数据预处理的目的

对数据进行预处理，求出数据的标准差和均值，对数据进行预处理上，对 x 进行预处理， 将 x 的值缩放到[-1,1]之间，即一个归一化的操作，让计算更加方便这样便于在后来的梯 度下降中，提高效率，而且 x 更好的收敛.

3. 梯度下降

之前，你对一个单变量回归问题实现了梯度下降。唯一的区别是矩阵 x 中还有一个特征， 假设函数仍然是$$h_{\theta }(x)={\theta }^{T}x=\sum _{i=0}^n{\theta }_i{x}_i$$
批量梯度下降更新规则是:
$${\theta }_j:={\theta }_j-a\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}（forallj）$$

初始化参数：θ=0
使用不同的学习率，即步长，实现梯度下降。由于 matlab 的矢量索引从 1 开始，而不是 0，因此在 matlab 中使用 theta,theta1，theta2，theta3，表示${\theta }_0,{\theta }_1,{\theta }_2,{\theta }_3$
初始化参数：${\theta }_0=0,{\theta }_1=0,{\theta }_2=0,{\theta }_3=0$

然后从初始化值开始进行梯度下降的一次迭代计 算，记录下这次迭代计算的结果${\theta }_0,{\theta }_1,{\theta }_2,{\theta }_3$
继续进行多次的梯度下降迭代计算，直到 θ收敛， θ收敛后，记录下最后的${\theta }_0,{\theta }_1,{\theta }_2,{\theta }_3$

4. 选择学习率使用 J(θ)

选择学习率α，目标是在范围内选择较好的学习率 0.001 ≤ α ≤ 10.

您将通过进行初始选择、运行梯度下降和观察损失函数，并相应地调整学习率来实现这一点。 回想一下，损失函数被定义为$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$

损失函数也可以写成以下向量化的形式:

$$J(\theta )=\frac{1}{2m}(X\theta -y{)}^T(X\theta -y)$$
其中：$$y=\left[\begin{array}{c}{y}^{(1)}\\ y^{(2)}\\ .\\ .\\ .\\ y^{(m)}\end{array}\right]$$
$$X=\left[\begin{array}{c}(x^{(1)}{)}^T\\ (x^{(2)}{)}^T\\ .\\ .\\ .\\ (x^{(m)}{)}^T\end{array}\right]$$

当使用像 Matlab/Octave 这样的数值计算工具时，向量化版本是有用和有效的。如果你熟悉 矩阵，你可以证明这两种形式是等价的。 在前面的练习中，在θ0 和θ1 值的网格上计算 J（θ），现在将使用当前梯度下降阶段的 θ计算 J。 多步计算之后，您将看到 J（θ）如何随着迭代的推进而变化。 现在，以初始学习率运行大约 50 次迭代的梯度下降。 在每次迭代中，计算 J（θ）并将 结果存储在向量 J 中。 在最后一次迭代之后，根据迭代次数绘制 J 值。 在 Matlab/Octave 中，步骤是这样：

figure;%new figure 
theta=zeros(size(x(1,:)))'; 
alpha=0.1; 
J=zeros(50,1); 
for num_iterations=1:50;
	J(num_iterations)=loss(theta,x,y);
	theta=iteration(theta,alpha,y,x); 
end 
plot(0:49,J(1:50),'g-'); 
xlabel('iterations'); 
ylabel( 'J Cost ' );

如果你选择的学习率在一个良好的范围内，你的图应该如下图所示。

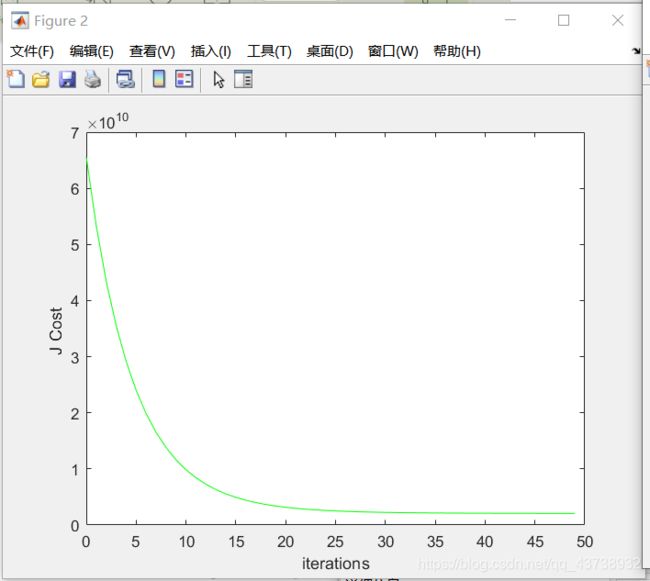
如果你的图表看起来很不一样，特别是如果你的 J（θ）值增加甚至爆炸，调整你的学习速 率，然后再试一次。 我们建议以 3 倍于下一个最小值(即 0.01,0.03,0.1,0.3 等等)。 你可能 还希望调整正在运行的迭代次数，如果这将帮助您看到曲线中的总体趋势的话。

为了比较不同的学习学习率对收敛性的影响，我们可以将几种学习学习率的 J 绘制在同一幅 图上。在 Matlab/Octave 中，这可以通过在绘图之间使用 hold on 命令执行多次梯度下降来 实现。具体地说，如果你已经尝试了三个不同的 alpha 值(你可能应该尝试更多的值)并将成 本存储在里面 J1、J2 和 J3，您可以使用以下命令将它们绘制在同一图上:

figure; 
plot(0:49,J(1:50),'b-'); 
hold on;%put them in the same figure 
plot(0:49,J1(1:50),'r-'); 
plot(0:49,J2(1:50),'k-'); 
plot(0:49,J3(1:50),'g-'); 
xlabel('iterations'); 
ylabel(' Cost J ');

结果图

5.问题解答

1. 回答下列问题：
   a. 观察随着学习率的变化，损失函数的变化。当学习率太小时会发生什么？太大呢？
   b. 使用你发现的最佳学习率，运行梯度下降，直到收敛以找到
   (A) θ的最终值
   (B) 一套 1650 平方英尺和 3 间卧室的房子的预测价格。 当你做出这个预测时，不要忘记缩放你的特征.

解：
a. 由下面的图片可以观察，当α取不同值时，cost 与迭代次数的曲线关系图。 蓝色α=0.01 ，红色α= 0.05， 绿色α=0.5 ，黑色α=0.1。

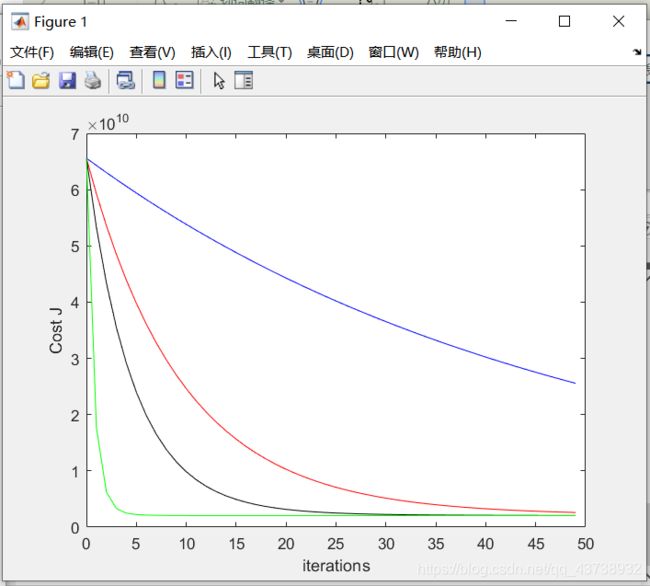
修改α的值，会发现如下变化：
蓝色α=0.01 ，红色α=0.1 ， 黑色α=0.8 ， 绿色α=1。

当α=2时，损失函数发散，不再收敛。

因此，我们得出结论，当学习率过大时，会造成损失函数发散。学习率过小时，损失函数收敛性不好。

b.最佳学习率α=0.1。θ的最终值是$$\begin{gathered} 1.0e+0.5\ast \\ 3.3866 \\ 1.0413 \\ -0.0017 \end{gathered}$$

预测房子的价格为2.9275e+05

2.正规方程
在正规方程的中，你学过最小二乘拟合的封闭解是
$$\theta =(X^{T}X{)}^{-1}{X}^{T}y.$$
使用这个公式不需要任何特征缩放，而且你将在一次计算中得到一个精确的解:不存在像梯度下降那样的“直到收敛为止的循环”。
a.在你的程序中，用上面的公式计算θ。 请记住，虽然你不需要缩放你的功能，但你仍然需要添加一个拦截项。
b.一旦你从这个方法中找到θ，就用它来预测一个1650平方英尺的房子，有3间卧室。 你得到的价格和你通过梯度下降发现的一样吗？

解：
a.结果图如下，通过正规方程计算出来的θ的值为
$$\begin{gathered} \theta =1.0e+05\ast \\ 3.4041 \\ 1.1063 \\ -0.0665 \end{gathered}$$

b.房子的价格是：2.9308e+05。和我用梯度下降算出来的房价不一样，有差别。这是因为迭代次数以及其他误差所造成的。
程序运行结果图：

Code

%load the data
x=load('ex2x.dat');
y=load('ex2y.dat');
m=47;%samples
x=[ones(m,1),x];%add one column
sigma=std(x);%standard deviation
mu=mean(x);%average value
x(:,2)=(x(:,2)-mu(2))./sigma(2);%compute
x(:,3)=(x(:,3)-mu(3))./sigma(3);
%initialize the data
[theta,theta1,theta2,theta3]=deal(zeros(size(x(1,:)))');
[alpha,alpha1,alpha2,alpha3] = deal(0.01,0.05,0.1,0.5);
[J,J1,J2,J3]=deal(zeros(50,1));
%define the function
h=@(x,theta) x*theta;
loss=@(theta,x,y) mean((h(x,theta)-y).^2)/2;
iteration=@(theta,alpha,y,x) theta-alpha*(x'*(h(x,theta)-y))/m;
%show different learning rates
for num_iterations=1:50
    J(num_iterations)=loss(theta,x,y);
    theta=iteration(theta,alpha,y,x);%0
    J1(num_iterations)=loss(theta1,x,y);
    theta1=iteration(theta1,alpha1,y,x);%1
    J2(num_iterations)=loss(theta2,x,y);
    theta2=iteration(theta2,alpha2,y,x);%2
    J3(num_iterations)=loss(theta3,x,y);
    theta3=iteration(theta3,alpha3,y,x);%3
end
figure;
plot(0:49,J(1:50),'b-');
hold on;%put them in the same figure
plot(0:49,J1(1:50),'r-');
plot(0:49,J2(1:50),'k-');
plot(0:49,J3(1:50),'g-');
xlabel('iterations');
ylabel(' Cost J ');
figure;%new figure
theta=zeros(size(x(1,:)))';
alpha=0.1;
J=zeros(50,1);
for num_iterations=1:50
    J(num_iterations)=loss(theta,x,y);
    theta=iteration(theta,alpha,y,x);
end
plot(0:49,J(1:50),'g-');
xlabel('iterations');
ylabel('J Cost ');
disp(theta);
%Data preprocessing
t1=(1650-mu(2))./sigma(2);
t2=(3-mu(3))./sigma(3);
disp(h([1,t1,t2],theta));
% regularization to avoid overfitting
%normal equation
u=(x'*x)\x'*y;
disp(u)
t1=(1650-mu(2))./sigma(2);
t2=(3-mu(3))./sigma(3);
disp(h([1,t1,t2],u));