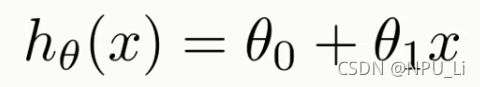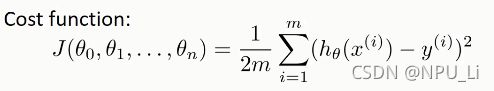机器学习(多元线性回归)
多元线性回归
一元线性回归是单特征(一个自变量,一个因变量),方程为:
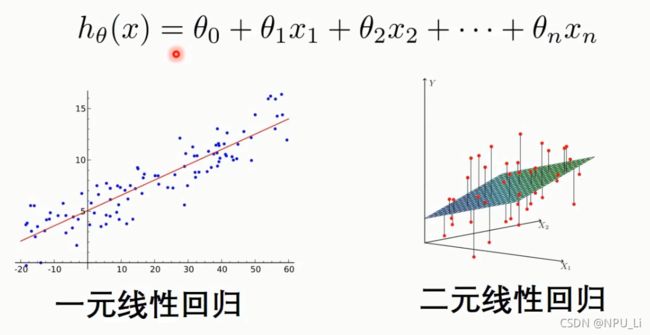
当考虑多个特征时,就得到了多元线性回归,方程为:
同一元线性回归,可以得到多元线性回归的cost function:
参数更新(左1,右>=1):
实战
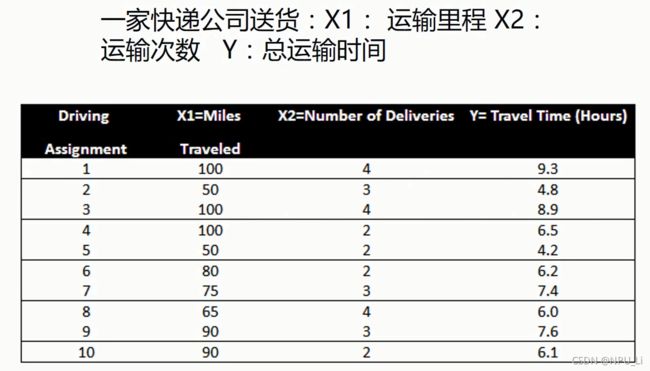
案例如下(二元线性回归):
方法一:梯度下降法
步骤一:导库、导数据
# 导入需要的库
import numpy as np
import matplotlib.pyplot as plt
#导入要进行回归的数据
data = np.genfromtxt(r"Delivery.csv",delimiter=',')
x_data = data[:,:-1]
y_data = data[:,-1]步骤二:编写算法
# 学习率+方程初始值+最大迭代次数
lr = 0.0001
theta0 = 0
theta1 = 0
theta2 = 0
epochs = 1000
# 最小二乘法
def compute_error(theta0, theta1, theta2, x_data, y_data):
totalError = 0
for i in range(0, len(x_data)):
totalError += (y_data[i] - (theta1 * x_data[i,0] + theta2*x_data[i,1] + theta0)) ** 2
return totalError / float(len(x_data))
def gradient_descent_runner(x_data, y_data, theta0, theta1, theta2, lr, epochs):
# 计算总数据量
m = float(len(x_data))
# 循环epochs次
for i in range(epochs):
theta0_grad = 0
theta1_grad = 0
theta2_grad = 0
# 计算梯度的总和再求平均
for j in range(0, len(x_data)):
theta0_grad += (1/m) * ((theta1 * x_data[j,0] + theta2*x_data[j,1] + theta0) - y_data[j])
theta1_grad += (1/m) * x_data[j,0] * ((theta1 * x_data[j,0] + theta2*x_data[j,1] + theta0) - y_data[j])
theta2_grad += (1/m) * x_data[j,1] * ((theta1 * x_data[j,0] + theta2*x_data[j,1] + theta0) - y_data[j])
# 更新b和k
theta0 = theta0 - (lr*theta0_grad)
theta1 = theta1 - (lr*theta1_grad)
theta2 = theta2 - (lr*theta2_grad)
return theta0, theta1, theta2第三步:运行,可视化(这里就不弄了)
theta0, theta1, theta2 = gradient_descent_runner(x_data, y_data, theta0, theta1, theta2, lr, epochs)方法二:sklearn
第一步:导库、导数据
# 导入需要的库
import numpy as np
import matplotlib.pyplot as plt
#导入要进行回归的数据
data = np.genfromtxt(r"Delivery.csv",delimiter=',')
x_data = data[:,:-1]
y_data = data[:,-1]第二步:创建模型并训练
# 创建模型
model = linear_model.LinearRegression()
model.fit(x_data, y_data)第三步:预测,可视化(这里就不弄了)
# 系数
print("coefficients:",model.coef_)
# 截距
print("intercept:",model.intercept_)
# 测试
x_test = [[102,4]]
predict = model.predict(x_test)
print("predict:",predict)这是我学习 覃秉丰老师的《机器学习算法基础》的自学笔记,课程在B站中的地址为:机器学习算法基础-覃秉丰_哔哩哔哩_bilibili