深入理解CV中的Attention机制之SE模块
CV中的Attention机制汇总(一):SE模块
Squeeze-and-Excitation Networks
论文链接:Squeeze-and-Excitation Networks
1. 摘要
In this work, we focus instead on the channel relationship and propose a novel architectural unit, which we term the “Squeeze-and-Excitation”(SE) block,that adaptively recalibrates(重新校准)channel-wise feature responses by explicitly modelling interdependencies between channels.
SE模块属于通道注意力机制,可以自适应学习不同通道之间的依赖关系。
2. SE模块详细理解
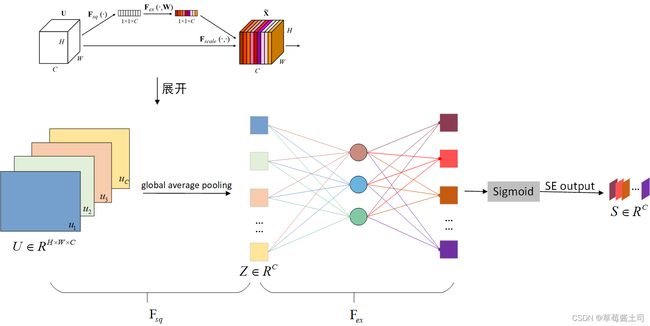
原文中给出的SE模块图例如下:
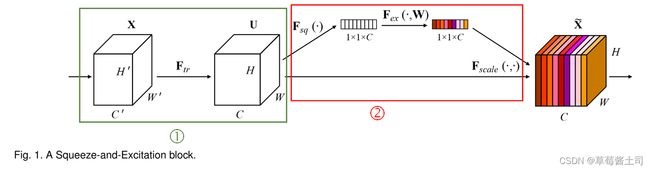
结合论文第3节的内容对以下两个问题进行详细理解:
- SE模块是如何学习不同通道之间的依赖关系的?
- SE模块是如何利用通道信息引导模型对特征进行有区分度的加权学习的?
2.1 多输入与多输出通道
图1中①部分描述了多输入与多输出通道的卷积层.
多输入通道:输入特征图的每个通道都对应一个二维卷积核,所有输入通道的卷积结果之和为最后的卷积结果,如下图所示(为了简便描述,省略了偏差):
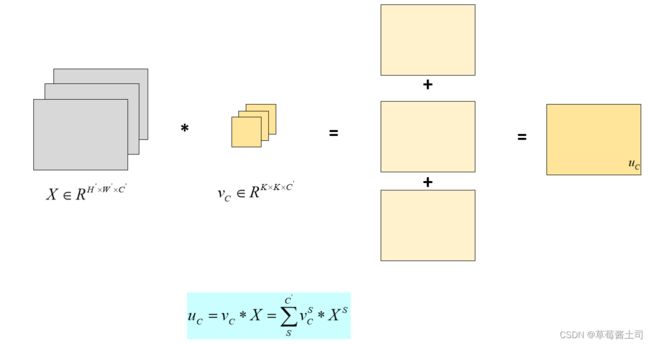
式中, C C C表示第 C C C个输出通道, S S S表示第 S S S个输入通道。
每个输入通道均对应一个二维卷积核,所以:三维卷积核的通道数=输入特征图的通道数.
2.2 多输出通道
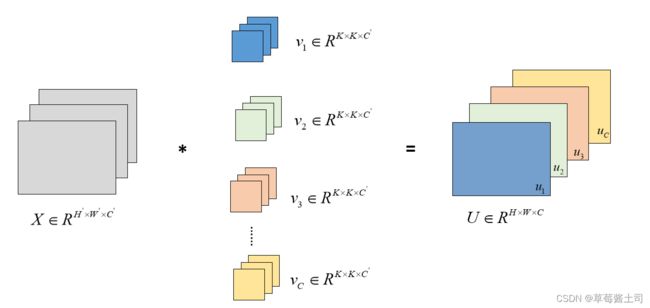
每个输出通道对应独立的三维卷积核,因此,输出特征图的通道数=三维卷积核的个数。通常,输出通道数是超参数。
根据多输入与多输出通道的原理,我们不难理解在常规的卷积计算中,不同输入通道之间的关联性隐藏于每个输出通道中,且仅采用“相加”这一简单的方式,而不同的输出通道对应于独立的三维卷积核,因此,输入通道之间的关联性没有得到合理的利用。
因此论文作者提出SE模块来显式地利用不同输入通道之间的信息。
2.3 Squeeze-and-Excitation Block
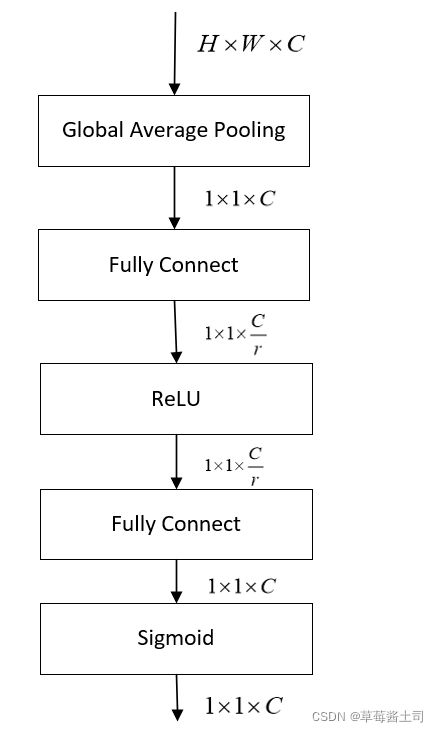
2.3.1 Squeeze: Global Information Embedding
作者采用全局平均汇聚(Global Average Pooling)得到每个通道的信息。
z c = F s q ( u c ) = 1 H × W ∑ i = 1 H ∑ j = 1 W u c ( i , j ) z_c=\bold F_{sq}(\bold u_c)=\frac{1}{H\times W}\sum_{i=1}^{H} \sum_{j=1}^{W}u_c(i,j) zc=Fsq(uc)=H×W1i=1∑Hj=1∑Wuc(i,j)
为什么这么做?原文中解释道:
Each of the learned filters operates with a local receptive field and consequently each unit of the transformation output U U U is unable to exploit contextual information outside of this region.
在一张大小为 H × W H\times W H×W的特征图中,每个元素仅对应输入特征图中的某个局部区域(即感受野),因此输出特征图中的每个元素仅包含了局部信息而不是全局信息。
To mitigate this problem, we propose to squeeze global spatial information into a channel descriptor. This is achieved by using global average pooling to generated chanel-wise statistics.
作者采用全局平均汇聚得到每个通道的全局特征,目的是为了融合局部信息得到全局信息,之所以采用全局平均汇聚是因为实现简单,也可以采用其他更为精细但复杂的操作。
2.3.2 Excitation: Adaptive Recaloibration
Excitation(激励)模块是为了更好地得到各个通道之间的依赖关系,需要满足两个要求:
- 可以学习各个通道之间的非线性关系;
- 可以保证每个通道都有对应的输出,得到soft-label,而不是one-hot型向量。
因此,作者使用了两个全连接层学习非线性关系,最后使用sigmoid激活函数。
并且为了降低模型参数和复杂度,采用了“bottleneck”思想设计全连接层,随之产生一个超参数: r r r,文中令 r = 16 r=16 r=16。
关 于 为 什 么 使 用 s i g m o i d 函 数 的 思 考 ? \color{red}{关于为什么使用sigmoid函数的思考?} 关于为什么使用sigmoid函数的思考?
sigmoid是常见的激活函数之一,SE模块最后的输出相当于学习到的每个通道的权重,首先要保证权重不能为0,为0的话反而会损失大量信息,因此不能使用ReLU;另外,这里想要得到范围在 [ 0 , 1 ] [0,1] [0,1]的权重,而不是为了突出某一个通道,有别于“多类别分类”问题,更像“多标签分类”问题,因此这里使用softmax函数是不合适的。
Excitation模块公式表示:
s = F e x ( x , W ) = σ ( g ( z , W ) ) = σ ( W 2 δ ( W 1 z ) ) s=\bold F_{ex}(\bold x, \bold W)=\sigma(g(\bold z,\bold W))=\sigma(\bold W_2\delta(W_1 \bold z)) s=Fex(x,W)=σ(g(z,W))=σ(W2δ(W1z))
式中, δ ( ∙ ) \delta(\bullet) δ(∙)表示ReLU激活函数, σ ( ∙ ) \sigma(\bullet) σ(∙)表示sigmoid激活函数。
2.3.3 加权
最后将SE模块的输出作用于卷积层的输出,得到通道注意力加权的输出特征图。
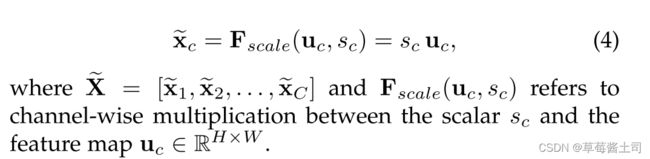
使用得到的channel-wise向量,对每个通道的特征图的每个元素作加权(理解公式(4)后面是标量与矩阵的乘积)。
3. SE模块的使用
三、PyTorch实现SE模块
3.1 使用全连接层实现Excitation
class SE(nn.Module):
def __init__(self, channels, reduction=16): # 这里默认为16,如果特征图通道数较小,可以适当调整
super(SE, self).__init__()
self.squeeze = nn.AdaptiveAvgPool2d((1, 1))
self.excitation = nn.Sequential(
nn.Linear(channels, channels // reduction, bias=False),
nn.ReLU(inplace=True),
nn.Linear(channels // reduction, channels, bias=False),
nn.Sigmoid())
def forward(self, x):
b, c, _, _ = x.size()
y = self.squeeze(x).view(b, c)
y = self.excitation(y).view(b, c, 1, 1)
return x * y.expand_as(x)
3.2 使用 1 × 1 1\times 1 1×1卷积实现Excitation
使用 1 × 1 1\times 1 1×1卷积代替全连接层,避免矩阵与向量之间的维度转换
class SE(nn.Module):
def __init__(self, channels, reduction=2):
super(SE, self).__init__()
self.squeeze = nn.AdaptiveAvgPool2d((1, 1))
self.excitation = nn.Sequential(
nn.Conv2d(channels, channels // reduction, kernel_size=1, stride=1, padding=0, bias=False),
nn.ReLU(inplace=True),
nn.Conv2d(channels // reduction, channels, kernel_size=1, stride=1, padding=0, bias=False),
nn.Sigmoid())
def forward(self, x):
b, c, _, _ = x.size()
y = self.squeeze(x)
print(y.shape)
y = self.excitation(y)
print(y.shape)
return x * y