HMM模型

HMM：隐马尔可夫模型

最大熵模型

熵在信息论中学过，表现的是系统所处状态的不确定性程度。表示的是这个信息系统的平均信息量也即平均不确定程度。
最大熵模型（the maximum entropy principle）是指保留全部的不确定性将风险降低到最小。例如根据拼音wang-xiao-bo可以转换为王小波（作者）和王晓波（研究两岸关系的学者），但是具体转换为谁应当根据上下文确定。因此我们建立一个最大熵模型，使得同时满足这两种信息。香农奖得主数学家希萨（Csiszar）证明了对于任何一组不自相矛盾的信息，这个最大熵模型不仅存在且唯一。并且都有一个非常简单的形式——指数函数。
最大熵模型最早在实际信息处理应用中被验证优势了的是原IBM研究员拉萨帕提将上下文信息、词性（名词、动词和形容词等）、句子成分（主谓宾）通过最大熵模型结合起来，做出了当时世界上最好的词性标识系统和句法分析器。但是最大熵模型有很大很大的计算量，形式简单但是实现复杂。

HMM

隐马尔可夫模型（Hidden Markov Model）是统计模型，用来描述一个含有隐含未知参数的马尔可夫过程。是在被建模的系统被认为是一个马尔可夫过程与未观测到的状态的统计马尔可夫模型。
举一个例子描述则：

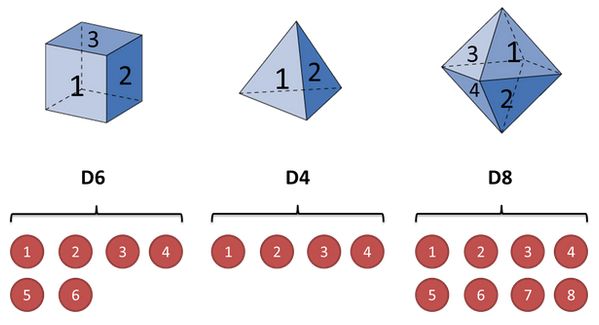
假设手中有三个不同的骰子，分别为六面体、四面体、八面体，各面出现几率相同均为1/6,1/4,1/8

然后开始掷骰子，得到一串数字：1-6-8-4-5
这串数字叫做可见状态链，但是在HMM中不仅仅有这么一串可见状态链还有一串隐含状态链，例如上面例子中的隐含状态链就是你用的骰子的序列：比如可以是：D4 D6 D8 D4 D6
一般来说HMM中说到的马尔可夫链就是指这个隐含状态链。在我们的例子中三个骰子概率均等，但是很多情况下是不等的。同样的，骰子中各个数值的出现概率也是如此。

对于HMM如果信息全部已知，比如所有隐含状态之间的转换概率和所有隐含状态下各个可见状态之间的输出概率都已知。那么做模拟是很容易的，但是应用HMM模型时候一般都是缺失了一部分信息的。我们应该做的就是应用算法去估计这些缺失的信息

和HMM相关的问题主要分为三类

• 知道隐含状态数量（骰子种类）、转换概率（骰子是几面/以及概率如何分布）、可见状态链（已知的骰子的投掷结果）。而我们想知道的就是每次掷出来的究竟是哪种骰子；解法是求最大似然状态路径，即求出最大概率出现这个可见状态链的骰子序列。
• 知道隐含状态数量、转换概率、可见状态链，求取掷出这个结果的概率；这个问题可以用来检测观察到的结果是否与已知模型吻合，多次实验可以验证模型是否正确。
• 知道隐含状态数量、可见状态链，不知道转换概率，而解决的问题是反推出每种骰子是什么类型的骰子；这是最为常见的情况，这个时候需要从可见结果种估计参数。

第一类问题，求解最大似然路径：

暴力法直接穷举所有可能的骰子序列，然后依照概率直接算出每种序列的概率是多少，这个方法当马尔科夫链短的时候可行，但是长的话很难完成。有一种很有名的方法叫：Viterbi 算法
介绍该算法前先考虑一下如何求得最大概率路径
假如按照第一类的已知情况掷出的结果为1-6-3：
首先掷第一次时：

得到结果为1，那么推测该骰子序列为D4，因为D4产生1的概率比D6\D8都大为1/4,同理考虑掷第二次骰子时：

得到1-6这个结果时，如果想使概率保持最大，相应的取第二次的骰子为D6，于是此时的概率计算公式为
$$P2(D6)=P(D4)\ast P(D4->1)\ast P(D4->D6)\ast P(D6->1)=1/3\ast 1/4\ast 1/3\ast 1/6$$
于是此时得到的最大概率序列为：D3 D6
同理第三次掷出3这个结果，那么也应是取D4才可以保证概率值达到最大。我们可以总结出规律，无论马尔可夫链多长，我们都可以从第一个骰子开始为取得最大概率得出应该取哪个骰子，长度增加时前面序列保持不变再追加新的骰子序列即可。

第二类问题：模型与现实相印证

如果我怀疑自己的骰子被动了手脚该怎么办？例如本该六面出现概率相同被改造成出现1的概率为1/2，这时我们选择算一算正常的三个骰子掷出一段序列的概率，再算一算（一个不正常的骰子+两个正常的骰子的概率）如果出现明显偏差，那就是出了问题：
仍然假设投掷三次的结果是1-6-3，我们计算思路是算出各个情况下掷出1-6-3的概率再进行加和，因为需要模拟实验，不做赘述

Viterbi 算法

HMM是用来描述隐含未知参数的统计模型，即解决第三类问题。另举一个经典例子：一位东京的朋友根据天气情况{下雨,天晴}决定当天活动{散步，购物，宅家}中的一种。已知这个人前三天的情况为：散步-购物-宅家，那么我们如何推断这三天东京的天气情况。这个例子中显示状态为活动，隐状态是天气。
每一个HMM可以通过以下五元组描述：

:param obs:观测序列——{散步-购物-宅家}
:param states:隐状态——{三种活动}
:param start_p:初始概率（隐状态）——{晴天的概率，雨天的概率}
:param trans_p:转移概率（隐状态间的转换概率）
:param emit_p:发射概率（根据天气选择活动的概率）
伪代码：
start_probability = {'Rainy': 0.6, 'Sunny': 0.4}
 
transition_probability = {
    'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},
    'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},
    }
 
emission_probability = {
    'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
    'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
}

而我们的问题就是求解最可能的隐状态序列，通常用到Viterbi算法，也就是上述提到的求解最大路径算法，但是存在不同之处。上述的最大路径算法由于每次骰子的选取都是不相关的，独立的。因此可以利用贪心算法求解，但是这个不同。
首先第一天的天气很容易计算，因为第一天出去散步了：
$$P(第一天)(下雨)=初始概{率}_{下}雨\ast 发射概{率}_{散}步=0.6\ast 0.1=0.06P(第一天)(天晴)=初始概{率}_{天}晴\ast 发射概{率}_{散}步=0.4\ast 0.6=0.24$$
所以第一天是晴天的概率比较大。
从第二天开始，对于每种天气Y，都要计算前一天的天气X到Y的转换概率。属于累乘的结果，因此我们此例中第一天的对于第二天的天气Y有两种结果，X也有两种结果，Y也有两种结果。
如图所示，先求取出当第二天天气是Q（晴天）和Y（雨天）时，走哪条路径可以保证概率最大，然后将除概率最大的路径之外的路径删除，保留两条备用路径即：Q-Q与Y-Y，再根据Q与Y到购物（B)的路径上的概率的连乘哪个更大就是第二天选择购物时的最大概率路径。
整个过程是一个动态规划的过程，牵涉到不够优的路径的删除。

这是第二天的序列选取，经过这次选取应当确定两条备用路径，分别代表Y值为雨天/晴天。然后以同样的方式去算第三天的概率，找出最终结果。

参考文献

[博客园]：一文搞懂HMM（隐马尔可夫模型）https://www.cnblogs.com/skyme/p/4651331.html
[知乎]：如何通俗地讲解 viterbi 算法？ - 路生的回答 - 知乎
https://www.zhihu.com/question/20136144/answer/763021768