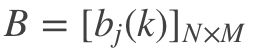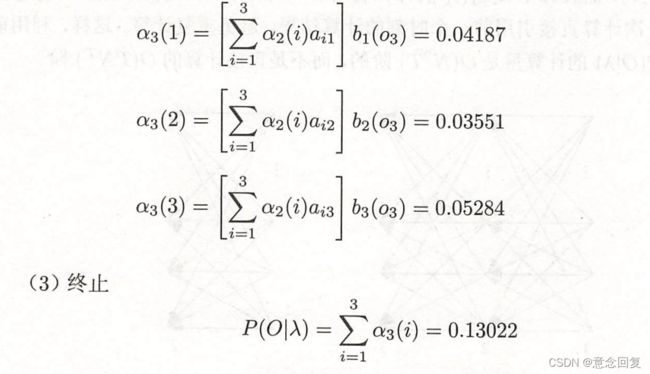机器学习算法（十七）：隐马尔科夫模型（HMM）

目录

1 隐马尔科夫模型

1.1 模型概念

1.2 定义

1.3 隐马尔科夫模型的两个性质

1.4 盒子与球模型

1.5 三个基本问题

2 概率计算算法

2.1 直接计算法

2.2 前向算法

2.3 后向算法

2.4 一些概率与期望值的计算

3 学习算法

3.1 监督学习方法

3.2 Baum-Welch算法

3.3 Baum-Welch模型参数估计公式

4 预测算法

4.1 近似算法

4.2 维比特算法

5 总结

马尔科夫链：机器学习算法（十六）：马尔科夫链_意念回复的博客-CSDN博客_马尔科夫链算法

1 隐马尔科夫模型

1.1 模型概念

        隐马尔可夫模型（Hidden Markov Model，HMM）是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析，例如模式识别。是在被建模的系统被认为是一个马尔可夫过程与未观测到的（隐藏的）的状态的统计马尔可夫模型。

        举个例子，假设你有一个住得很远的朋友，他每天跟你打电话告诉你他那天做了什么，你的朋友仅仅对三种活动感兴趣：公园散步，购物以及清理房间。他选择做什么事情只凭天气，你对于他所住的地方的天气情况并不了解，但是你知道总的趋势。在他告诉你每天所做的事情基础上，你想要猜测他所在地的天气情况。其实这个就是一个隐马尔科夫模型。每一天天气的变化就是一个隐马尔科夫链(即不同状态之间的转换)，其有两个状态 “雨"和"晴”，但是你无法直接观察它们，也就是说，它们对于你是隐藏的。每天，你的朋友有一定的概率进行下列活动：“散步”， “购物”，或 “清理”。因为你朋友告诉你他的活动，所以这些活动就是你的观察数据。这整个系统就是一个隐马尔可夫模型HMM。

        对于上述的例子而言，如果连续持续多天，你的朋友可能根据不同的天气进行不同的活动(当然，这里有一个前提，你的朋友在同一天只能进行一种活动)，这几天天气的变化的就是一个隐藏的状态序列，比如说连续五天的天气为[‘晴’,‘雨’,‘雨’,‘晴’,‘雨’](这是在你不看天气预报的前提下),而你的朋友每一天做的活动就组成了观测序列。这样看起来是不是简单多了。

        有了上面的例子，下面可以对隐马尔可夫模型进行符号化的定义

1.2 定义

        隐马尔科夫模型有初始概率分布、状态转移概率分布以及观测概率分布确定，其形式化定义如下：

        设Q 是所有可能状态集合，V 是所有可能的观测的集

                

                其中N 是可能的状态数，M 是可能的观测数。

        I 是长度为T 的状态序列，O 是对应的观测序列。

               

        A是状态转移矩阵：

               

                 其中：

                        

                        表示的是t 时刻处于qi 的条件下在t+1时刻状态转移到qj 的概率。

        B是观测概率矩阵：

​​​​​​​                

                 其中：

                       

                         是在时刻t处于状态qj 的条件下生成观测vk的概率。

        π 是初始状态概率向量：

               

        其中：

              

        所以隐马尔科夫模型λ 可以用三元符号表示，即：

              

        状态转移矩阵A 和初始状态概率π 确定隐藏的马尔科夫链，生成不可观测的状态序列，观测概率矩阵B 确定了如何从观测状态生成观测序列。这里从wiki上面盗一张图，上面的x 即对应的状态序列，y 表示的是观测序列：

1.3 隐马尔科夫模型的两个性质

       (1) 齐次马尔科夫性假设，即使设隐藏的马尔科夫链在任意时刻t 的状态只依赖于前一时刻的状态，与其他时刻的状态以及观测无关。

               

         这句话是什么意思呢？以上面的图为例，假设x(t) 表示的状态是前面例子里面的天气，那么x(t+1)的天气与x(t−1) 的天气无关，只与x(t) 的天气有关。并且也与y(t+1) 无关。

        (2) 观测独立性假设，即假设任意时刻的观测只依赖该时刻的马尔科夫链的状态，与其他观测和状态无关。

                

        意思即为观测状态只与对应的有关。而与其他的状态无关。下面以一个具体例子帮助理解。

1.4 盒子与球模型

        假设有4个盒子，每一个盒子里面都装有红白两种颜色的球，盒子里面的红白求数有下面表格给出。    

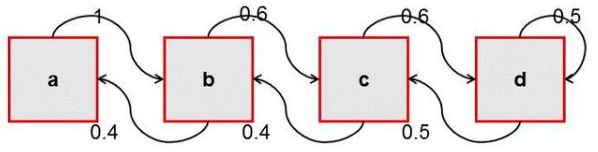
        按照下面的方法抽球，并且产生一个关于球的颜色观测序列：首先从四个盒子中等概率随机抽取一个球。记录颜色然后放回盒子，然后根据当前的概率随机转移到下一个盒子。规则是：若当前的状态为盒子a，那么接下来必然在盒子b中随机取球；若当前的状态为盒子b，那么接下来在盒子a中随机取球的概率为0.4，在盒子c中取球的概率为0.6；若当前的状态为盒子c，那么接下来在盒子b中随机取球的概率为0.4，在盒子d中取球的概率为0.6；若当前的状态为盒子d，那么接下来在盒子c中随机取球的概率为0.5，在盒子d中取球的概率为0.5。随机抽取一个球，如此重复5次，得到一个球的颜色的观察序列：

               

        上述过程中，球的颜色序列为观测序列，而抽取的盒子的序列为状态序列。为了清楚表示状态之间的转换，我们将抽盒子规则用马尔可夫链表示出来。

                 

        所以盒子对应的状态集合是：

                  

        球的颜色的观测集合为：

                  

        状态序列和观测序列的长度T=5 

        初始分布概率为  

        状态转移概率分布为

                 

        观测序列为

                 

1.5 三个基本问题

        马尔科夫模型的3个基本问题。

        (1) 概率计算问题。给定模型λ=(A,B,π) 和观测序列O=(o1,o2,...,oT) ，计算在模型λ 下观测序列为O 的概率P(O∣λ) 

        (2) 学习问题。已知观测序列O=(o1,o2,...,oT)，估计模型λ=(A,B,π) 的参数，使得在该模型下观测序列概率P(O∣λ) 最大。

        (3) 预测问题，也成为解码问题。已知模型λ=(A,B,π)和观测序列O=(o1,o2,...,oT) ，求对给定的观测序列概率P(I∣O) 的最大值。即给定观测序列，求最有可能的对应状态序列。

2 概率计算算法

2.1 直接计算法

 

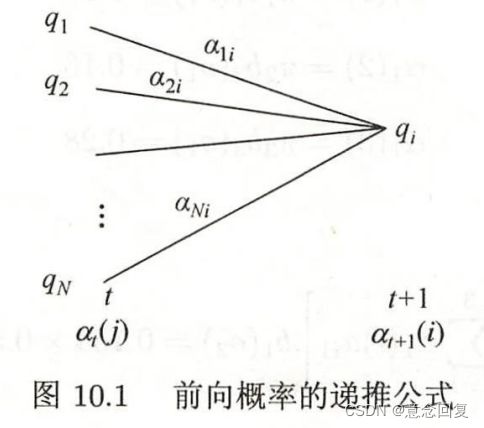
2.2 前向算法

        前向后向算法的核心是利用动态规划的思想减少计算的时间复杂度。

             

 

 

 

 

2.3 后向算法

 

 

2.4 一些概率与期望值的计算

 

 

 

3 学习算法

​​​​​​​

3.1 监督学习方法

 

3.2 Baum-Welch算法

 

 

 

3.3 Baum-Welch模型参数估计公式

 

 

4 预测算法

        预测问题是个什么问题呢？预测问题也叫做解码问题，即给定隐马尔科夫模型参数λ=(A,B,π)，以及观测序列，求P(I|O)，即最有可能出现的状态。

        解决上面的问题主要有两种方法，一种是近似算法，另外一种是维比特算法。

4.1 近似算法

​​​​​​​

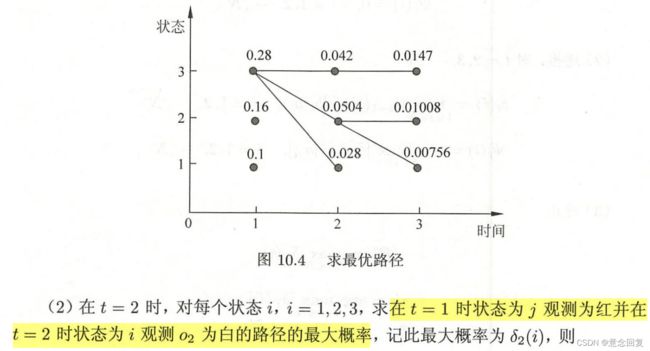
4.2 维比特算法

 

 

 

 

 

 

 

 

5 总结

​​​​​​​

 

《统计学习方法》，李航

隐马尔科夫模型一(概念理解)：隐马尔科夫模型一(概念理解)_gzj_1101的博客-CSDN博客_隐式马尔科夫

有趣的隐马尔科夫模型：百度安全验证