【机器学习】支持向量机

支持向量机

1、支持向量机介绍

在机器学习中，支持向量机(SVM，还支持矢量网络)是与相关的学习算法有关的监督学习模型，可以分析数据，识别模式，用于分类和回归分析。

支持向量机方法是建立在统计学习理论的VC维理论和结构风险最小原理基础上的，根据有限的样本信息在模型的复杂性（即对特定训练样本的学习精度）和学习能力（即无错误地识别任意样本的能力）之间寻求最佳折中，以期获得最好的推广能力。

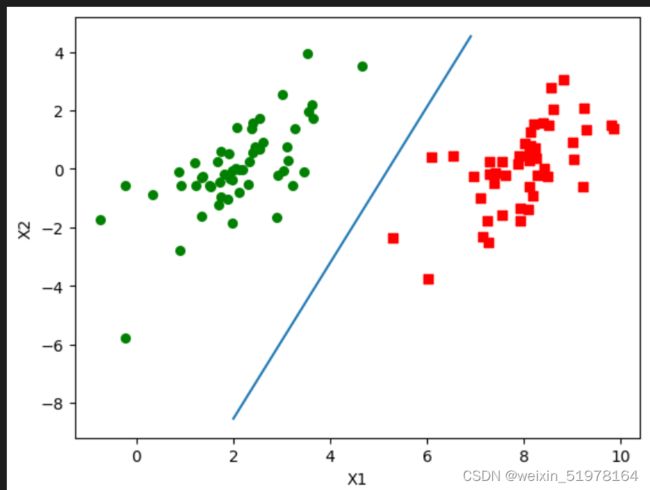
支持向量机将向量映射到一个更高维的空间里，在这个空间里建立有一个最大间隔超平面。在分开数据的超平面的两边建有两个互相平行的超平面。建立方向合适的分隔超平面使两个与之平行的超平面间的距离最大化。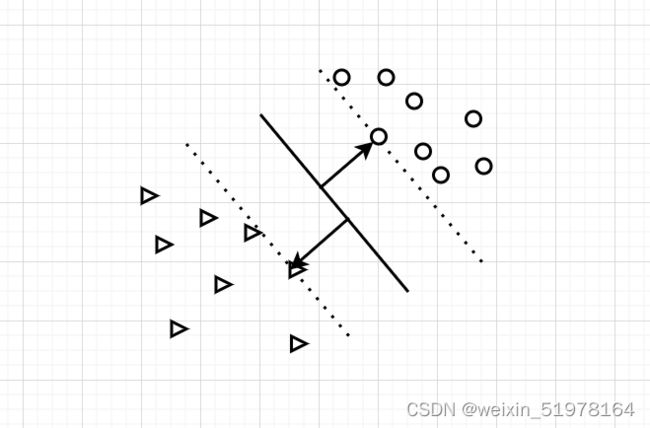
就是选择离中间那条线离上下两种类型的点的最近点的距离之和要最大。

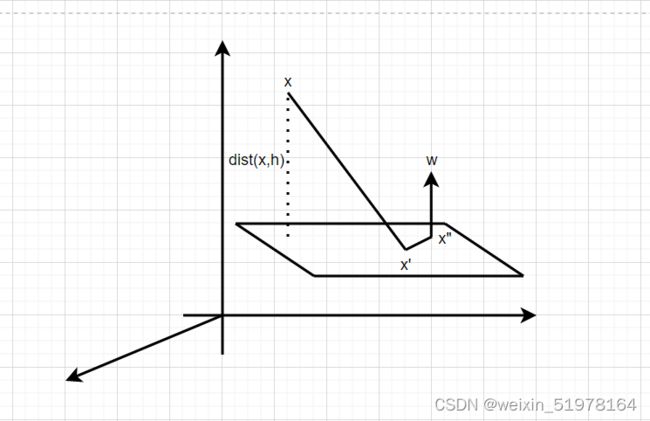
**然后可以拿出点到面的距离来分析公式，作平行线和xx’的投影平行，同时垂直于x’x",首先
之后直线的距离就是x-x’投影到这个面上的直线距离，所以公式如下；
**
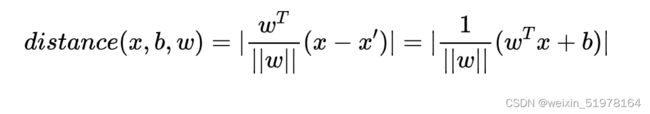
同时我们令Y为样本类别，当X为正例时 Y = 1,X为负例时Y= -1，那么对于决策方程来说y = wx +b，y(x)>0,y = 1 ; y(x)<0,y = -1，所以y(x)y>0,这样就是正数了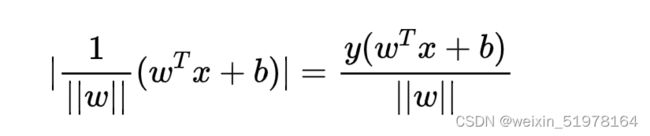
将绝对值去掉如上图；所以通过放缩在使得y(w^T+b)>1，优化目标函数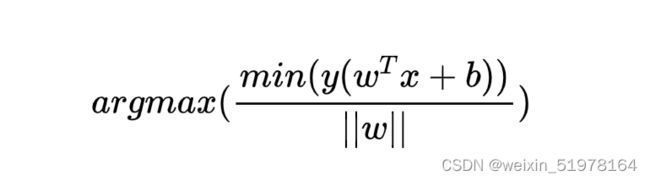
在这个条件下就只用考虑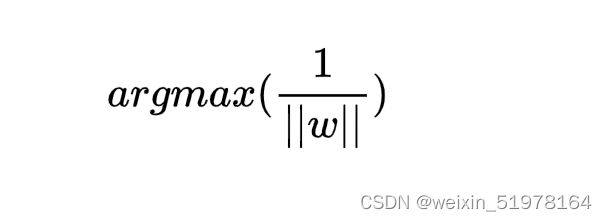
一般都是将极大值改为极小值算，所以上面求w最小值，也就是求如下公式的最小值。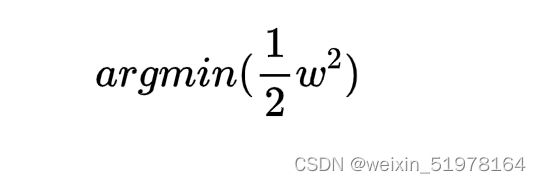
之后就可以用拉格朗日乘子法计算


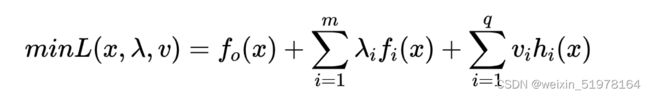
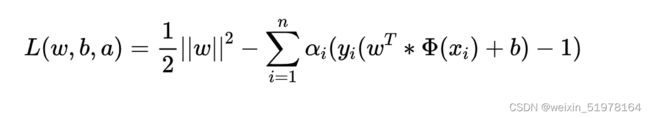
然后可以求出用w表示a,用b表示a,之后再把w,b用a来代替，最后就可以求出a,之后在把a代入w,b，这不就可以算出w了。

2、支持向量机简单实现

这个是SVM简单实现

# -*- coding: utf-8 -*-
__author__ = 'Wsine'

from numpy import *
import matplotlib.pyplot as plt
import operator
import time

def loadDataSet(fileName):
	dataMat = []
	labelMat = []
	with open(fileName) as fr:
		for line in fr.readlines():
			lineArr = line.strip().split('\t')
			dataMat.append([float(lineArr[0]), float(lineArr[1])])
			labelMat.append(float(lineArr[2]))
	return dataMat, labelMat

def selectJrand(i, m):
	j = i
	while (j == i):
		j = int(random.uniform(0, m))
	return j

def clipAlpha(aj, H, L):
	if aj > H:
		aj = H
	if L > aj:
		aj = L
	return aj

class optStruct:
	def __init__(self, dataMatIn, classLabels, C, toler):
		self.X = dataMatIn
		self.labelMat = classLabels
		self.C = C
		self.tol = toler
		self.m = shape(dataMatIn)[0]
		self.alphas = mat(zeros((self.m, 1)))
		self.b = 0
		self.eCache = mat(zeros((self.m, 2)))

def calcEk(oS, k):
	fXk = float(multiply(oS.alphas, oS.labelMat).T * (oS.X * oS.X[k, :].T)) + oS.b
	Ek = fXk - float(oS.labelMat[k])
	return Ek

def selectJ(i, oS, Ei):
	maxK = -1
	maxDeltaE = 0
	Ej = 0
	oS.eCache[i] = [1, Ei]
	validEcacheList = nonzero(oS.eCache[:, 0].A)[0]
	if (len(validEcacheList)) > 1:
		for k in validEcacheList:
			if k == i:
				continue
			Ek = calcEk(oS, k)
			deltaE = abs(Ei - Ek)
			if (deltaE > maxDeltaE):
				maxK = k
				maxDeltaE = deltaE
				Ej = Ek
		return maxK, Ej
	else:
		j = selectJrand(i, oS.m)
		Ej = calcEk(oS, j)
	return j, Ej

def updateEk(oS, k):
	Ek = calcEk(oS, k)
	oS.eCache[k] = [1, Ek]

def innerL(i, oS):
	Ei = calcEk(oS, i)
	if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
		j, Ej = selectJ(i, oS, Ei)
		alphaIold = oS.alphas[i].copy()
		alphaJold = oS.alphas[j].copy()
		if (oS.labelMat[i] != oS.labelMat[j]):
			L = max(0, oS.alphas[j] - oS.alphas[i])
			H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
		else:
			L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
			H = min(oS.C, oS.alphas[j] + oS.alphas[i])
		if (L == H):
			# print("L == H")
			return 0
		eta = 2.0 * oS.X[i, :] * oS.X[j, :].T - oS.X[i, :] * oS.X[i, :].T - oS.X[j, :] * oS.X[j, :].T
		if eta >= 0:
			# print("eta >= 0")
			return 0
		oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta
		oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
		updateEk(oS, j)
		if (abs(oS.alphas[j] - alphaJold) < 0.00001):
			# print("j not moving enough")
			return 0
		oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j])
		updateEk(oS, i)
		b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[i, :].T - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.X[i, :] * oS.X[j, :].T
		b2 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[j, :].T - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.X[j, :] * oS.X[j, :].T
		if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
			oS.b = b1
		elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]):
			oS.b = b2
		else:
			oS.b = (b1 + b2) / 2.0
		return 1
	else:
		return 0

def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup=('lin', 0)):
	"""
	输入：数据集, 类别标签, 常数C, 容错率, 最大循环次数
	输出：目标b, 参数alphas
	"""
	oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler)
	iterr = 0
	entireSet = True
	alphaPairsChanged = 0
	while (iterr < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
		alphaPairsChanged = 0
		if entireSet:
			for i in range(oS.m):
				alphaPairsChanged += innerL(i, oS)
			# print("fullSet, iter: %d i:%d, pairs changed %d" % (iterr, i, alphaPairsChanged))
			iterr += 1
		else:
			nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
			for i in nonBoundIs:
				alphaPairsChanged += innerL(i, oS)
				# print("non-bound, iter: %d i:%d, pairs changed %d" % (iterr, i, alphaPairsChanged))
			iterr += 1
		if entireSet:
			entireSet = False
		elif (alphaPairsChanged == 0):
			entireSet = True
		# print("iteration number: %d" % iterr)
	return oS.b, oS.alphas

def calcWs(alphas, dataArr, classLabels):
	"""
	输入：alphas, 数据集, 类别标签
	输出：目标w
	"""
	X = mat(dataArr)
	labelMat = mat(classLabels).transpose()
	m, n = shape(X)
	w = zeros((n, 1))
	for i in range(m):
		w += multiply(alphas[i] * labelMat[i], X[i, :].T)
	return w

def plotFeature(dataMat, labelMat, weights, b):
	dataArr = array(dataMat)
	n = shape(dataArr)[0]
	xcord1 = []; ycord1 = []
	xcord2 = []; ycord2 = []
	for i in range(n):
		if int(labelMat[i]) == 1:
			xcord1.append(dataArr[i, 0])
			ycord1.append(dataArr[i, 1])
		else:
			xcord2.append(dataArr[i, 0])
			ycord2.append(dataArr[i, 1])
	fig = plt.figure()
	ax = fig.add_subplot(111)
	ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
	ax.scatter(xcord2, ycord2, s=30, c='green')
	x = arange(2, 7.0, 0.1)
	y = (-b[0, 0] * x) - 10 / linalg.norm(weights)
	ax.plot(x, y)
	plt.xlabel('X1'); plt.ylabel('X2')
	plt.show()

def main():
	trainDataSet, trainLabel = loadDataSet("E:\\workplace\\testSet.txt")
	b, alphas = smoP(trainDataSet, trainLabel, 0.6, 0.0001, 40)
	ws = calcWs(alphas, trainDataSet, trainLabel)
	print("ws = \n", ws)
	print("b = \n", b)
	plotFeature(trainDataSet, trainLabel, ws, b)

if __name__ == '__main__':
	start = time.perf_counter()
	main()
	end = time.perf_counter()
	print('finish all in %s' % str(end - start))

3、支持向量机sklearn实现

这里我用的时sklearn里自带鸢尾花数据集，但是考虑到这里面标签分两类，所以我就把0，1分为一类，2自己一类。

from sklearn.svm import SVC#svc分类器
from sklearn import datasets

iris = datasets.load_iris()#读数据
X = iris['data'][:,(2,3)]#特征
y = iris['target']

setosa_or_versicolor = (y==0)|(y==1)#这个花有三类，转换成二分类问题，所以就拿0和1为一类
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]#各取索引
#训练操作
svm_clf = SVC(kernel = 'linear',C= float('inf'))#先拿线性举例子,C过拟合先不管无限大
svm_clf.fit(X,y)#传进去值

这边用了线性核函数，简单就是两个向量相乘，然后其中是先转置之后相乘，虽然他不像下面讲到的其他的核函数那样映射到高维，但是如果样本量巨大是那么，往往最简单的操作就是最好的，简单有效。

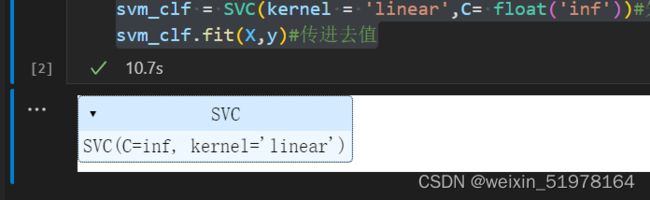
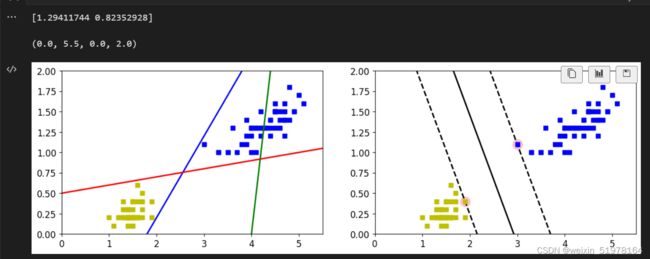
这里用一般模型来验证这个svm模型是否符合条件

#一般的模型
x0 = np.linspace(0,5.5,200)
pred_1 = 5*x0 - 20
pred_2 = x0 - 1.8
pred_3 = 0.1 *x0 +0.5

def plot_svc_decision_boundary(svm_clf,xmin,xmax,sv=True):#sv画不画支持向量
    w = svm_clf.coef_[0]#权重参数
    b = svm_clf.intercept_[0]#偏置参数
    print(w)
    x0 = np.linspace(xmin,xmax,200)
    decision_boundary = -w[0]/w[1]*x0 - b/w[1]#x0w0+x1w1+b = 0求x1
    #边界算完了然后就要算两个边界点到线的距离max
    margin = 1/w[1]     
    #指定两条虚线
    gutter_up = decision_boundary+margin
    gutter_down = decision_boundary-margin
    if sv:
        svs = svm_clf.support_vectors_
        plt.scatter(svs[:,0],svs[:,1] ,s = 180,facecolors = 'pink')
    #画决策边界
    plt.plot(x0,decision_boundary,'k-',linewidth = 2)#画直线,线条2好看些
    plt.plot(x0,gutter_up,'k--',linewidth = 2)#画虚线
    plt.plot(x0,gutter_down,'k--',linewidth = 2)
plt.figure(figsize=(14,4))#大小 
plt.subplot(121)#名字
plt.plot(X[:, 0][y==1],X[:,1][y==1],'bs ')
plt.plot(X[:, 0][y==0],X[:,1][y==0],'ys ')
plt.plot(x0,pred_1,'green',linewidth = 2)
plt.plot(x0,pred_2,'blue',linewidth = 2)
plt.plot(x0,pred_3,'red',linewidth = 2)

plt.axis([0,5.5,0,2])#坐标轴取值范围
plt.subplot(122)
plot_svc_decision_boundary(svm_clf,0,5.5)
plt.plot(X[:, 0][y==1],X[:,1][y==1],'bs ')
plt.plot(X[:, 0][y==0],X[:,1][y==0],'ys ')
plt.axis([0,5.5,0,2])

3.1、支持向量机sklearn实现–软间隔

防止异常点来破坏整体的函数布局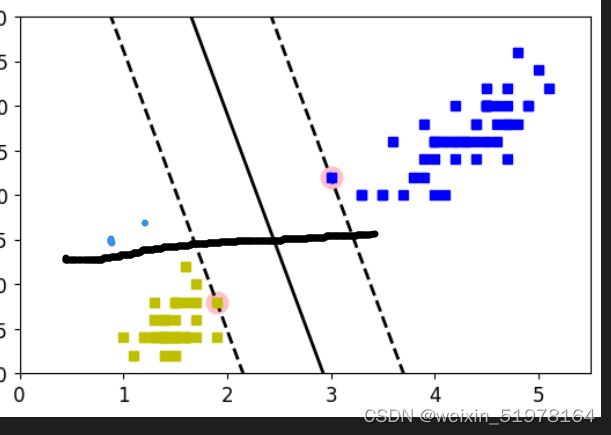
如上图，所以需要减少异常点带来的影响

#软间隔，防止过拟合，防止异常点导致的问题
import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline#流水线
from sklearn.preprocessing import StandardScaler#标准化
from sklearn.svm import LinearSVC

iris = datasets.load_iris()#读数据
X = iris['data'][:,(2,3)]#特征
y = (iris['target'] == 2).astype(np.float64)#选2类点

#构造流水线
svm_clf = Pipeline((
    ('std',StandardScaler()),
    ('linear_svc',LinearSVC(C = 1))
))#标准化操作

svm_clf.fit(X,y)

#我们看一下参数C值的取值对分类器的影响
scaler = StandardScaler()
svm_clf1 = LinearSVC(C = 1,random_state = 42)
svm_clf2 = LinearSVC(C = 100,random_state = 42)


scaler_svm_clf1 = Pipeline((
    ('std',StandardScaler()),
    ('linear_svc',svm_clf1)
))#标准化操作

 
scaler_svm_clf2 = Pipeline((
    ('std',StandardScaler()),
    ('linear_svc',svm_clf2)
))#标准化操作
scaler_svm_clf1.fit(X,y)
scaler_svm_clf2.fit(X,y)

scaler.fit(X,y)
b1 = svm_clf1.decision_function([- scaler.mean_ /scaler.scale_])
b2 = svm_clf2.decision_function([- scaler.mean_ /scaler.scale_])
w1 = svm_clf1.coef_[0]/scaler.scale_
w2 = svm_clf2.coef_[0]/scaler.scale_
svm_clf1.intercept_ = np.array([b1])
svm_clf2.intercept_ = np.array([b2])
svm_clf1.coef_ = np.array([w1])
svm_clf2.coef_ = np.array([w2])

plt.figure(figsize=(14,4.2))#大小 
plt.subplot(121)#名字
plt.plot(X[:, 0][y==1],X[:,1][y==1],'bs ',label = 'Iris-Virginica')
plt.plot(X[:, 0][y==0],X[:,1][y==0],'ys ',label = 'Iris-Versicolor')
plot_svc_decision_boundary(svm_clf1,4,6,sv = False)
plt.xlabel("Petal length",fontsize = 14)
plt.ylabel("Petal width",fontsize = 14)
plt.legend(loc="upper left",fontsize = 14)
plt.title("$C = {}$".format(svm_clf1.C),fontsize = 16)
plt.axis([4,6,0.8,2.8])

plt.subplot(122)#名字
plt.plot(X[:, 0][y==1],X[:,1][y==1],'bs ')
plt.plot(X[:, 0][y==0],X[:,1][y==0],'ys ')
plot_svc_decision_boundary(svm_clf2,4,6,sv = False)
plt.xlabel("Petal length",fontsize = 14)
plt.title("$C = {}$".format(svm_clf2.C),fontsize = 16)
plt.axis([4,6,0.8,2.8])

从这两者对比可以看出C在很小的情况下，这个间距就很大，错误率挺多的，然后C在很小的情况下，这个错误率就少了很多，但是间距就很小了，所以，很多时候我们要尽可能选择小的，虽然错误率多点，但是可以降低过拟合的风险，可以适当的减小C,不用那么严格。

3.2、支持向量机sklearn实现–核函数

3.2.1、支持向量机sklearn实现–核函数（线性）

线性核函数在上面那个软间隔那里其实就是以线性kernel = 'linear’实现的，所以具体如上方面的代码

3.2.2、支持向量机sklearn实现–核函数（多项式）

生成半环形数据集，以此来做对比（kernel = ‘ploy’）

from sklearn.datasets import make_moons
X,y = make_moons(n_samples=100,noise=0.15,random_state=42)
def plot_dataset(X,y,axes):
    plt.plot(X[:, 0][y==0],X[:,1][y==0],'bs ')
    plt.plot(X[:, 0][y==1],X[:,1][y==1],'ys ')
    plt.axis(axes)
    plt.grid(True,which='both')
    plt.xlabel(r"$x_1$",fontsize = 20)
    plt.ylabel(r"$x_2$",fontsize = 20,rotation = 0)

plot_dataset(X,y,[-1.5,2.5,-1,1.5])
plt.show()

from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline#流水线
from sklearn.preprocessing import PolynomialFeatures#标准化

prlynomial_svm_clf = Pipeline((('ploy_features',PolynomialFeatures(degree = 3)),
    ('scaler',StandardScaler()),
    ('svm_clf',LinearSVC(C = 10,loss = 'hinge'))
))#标准化操作
prlynomial_svm_clf.fit(X,y)

def plot_predictions(clf,axes):
    x0s = np.linspace(axes[0],axes[1],100)
    x1s = np.linspace(axes[2],axes[3],100)
    x0,x1 = np.meshgrid(x0s,x1s)
    X = np.c_[x0.ravel(),x1.ravel()]#拉长一下   
    y_pred = clf.predict(X).reshape(x0.shape)
    plt.contourf(x0,x1,y_pred,cmap = plt.cm.brg,alpha = 0.2)

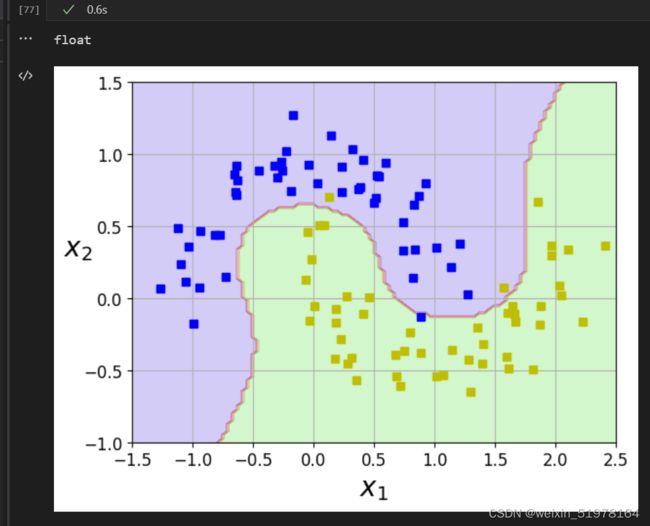
plot_predictions(prlynomial_svm_clf,[-1.5,2.5,-1,1.5])
plot_dataset(X,y,[-1.5,2.5,-1,1.5])
float

3.2.3、支持向量机sklearn实现–核函数（高斯核函数或者径向基函数）

因为在大多数情况下前两种都是用很少的，而且可以在多项式核函数基础上完善之后就类似高斯核函数，所以就详细将高斯核函数。还是先接上面那个半圆形的分析刚好可以更全面点，后面是用圆圈数据集，因为，圆圈和数据集不好分成两类，后面高斯核函数就直接升维，比如二维不好分，三维可能就好分了。

def gaussian_rbf(x,landmark,gamma):
    return np.exp(-gamma*np.linalg.norm(x - landmark,axis = 1)** 2)
gamma = 0.3
x1s = np.linspace(-4.5,4.5,200).reshape(-1,1)
x2s = gaussian_rbf(xls,-2,gamma)
x3s = gaussian_rbf(xls,1,gamma)

XK = np.c_[gaussian_rbf(X1D,-2,gamma),gaussian_rbf(X1D,1,gamma)]
yk = np.array([0,])

rbf_kernel_svm_clf = Pipeline([
    ('scaler',StandardScaler()),
    ('svm_clf',SVC(kernel = 'rbf',gamma = 5,C = 5))
])
rbf_kernel_svm_clf.fit(X,y)

from sklearn.svm import SVC
gamma1,gamma2 = 1 , 100
C1,C2 = 1 , 100
hyperparams = (gamma1,C1),(gamma1,C2),(gamma2,C1),(gamma2,C2)

svm_clfs = []
for gamma ,C in hyperparams:
    rbf_kernel_svm_clf = Pipeline([
        ('scaler',StandardScaler()),
        ('svm_clf',SVC(kernel = 'rbf',gamma = gamma,C = C))
    ])
    rbf_kernel_svm_clf.fit(X,y)
    svm_clfs.append(rbf_kernel_svm_clf)

plt.figure(figsize=(11,7))

for i ,svm_clf in enumerate(svm_clfs):
    plt.subplot(221+i)
    plot_predictions(svm_clf,[-1.5,2.5,-1,1.5])
    plot_dataset(X,y,[-1.5,2.5,-1,1.5])
    gamma ,C = hyperparams[i]
    plt.title(r"$\gamma = {},C = {}$".format(gamma,C),fontsize = 16)

plt.show()

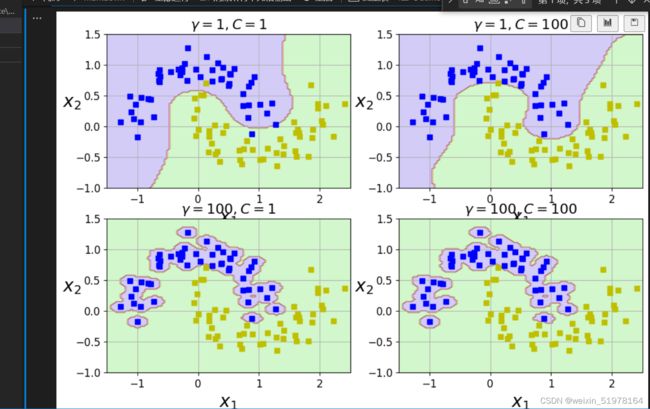
将kernel改成rbf同时又加上一个gamma值，这几幅图容易分析，上面几幅图可以看见，在C相同的情况下，gamma越小，那么这个辐射范围就越小，过拟合风险就越小，反着，gamma越大，辐射范围就越大，过拟合风险就越大，你看上面的gamma=100,如果再加几个可能就不是这个范围了，所以分类问题主要就是靠交叉验证来选择这个合适的参数的

from sklearn.svm import SVC
# 生成数据集
from sklearn.datasets import make_blobs, make_circles
from matplotlib import pyplot as plt
import numpy as np
from mpl_toolkits import mplot3d




def plot_SVC_decision_function(model, ax=None, plot_support=True):
    '''Plot the decision function for a 2D SVC'''
    if ax is None:
        ax = plt.gca()  # get子图
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()

    # create grid to evaluate model
    x = np.linspace(xlim[0], xlim[1], 30)
    y = np.linspace(ylim[0], ylim[1], 30)
    # 生成网格点和坐标矩阵
    Y, X = np.meshgrid(y, x)
    # 堆叠数组
    xy = np.vstack([X.ravel(), Y.ravel()]).T
    P = model.decision_function(xy).reshape(X.shape)

    # plot decision boundary and margins
    ax.contour(X, Y, P, colors='k', levels=[-1, 0, 1],
               alpha=0.5, linestyles=['--', '-', '--'])  # 生成等高线 --

    # plot support vectors
    if plot_support:
        ax.scatter(model.support_vectors_[:, 0],
                   model.support_vectors_[:, 1],
                   s=300, linewidth=1, facecolors='none')

    ax.set_xlim(xlim)
    ax.set_ylim(ylim)


def train_svm_plus():
    # 二维圆形数据 factor 内外圆比例（0， 1）
    X, y = make_circles(100, factor=0.1, noise=0.1)
    # 加入径向基函数
    clf = SVC(kernel='rbf')
    clf.fit(X, y)

    plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
    plot_SVC_decision_function(clf, plot_support=False)
    plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
                s=300, lw=1, facecolors='none')
    return X, y


def plot_3D(X, y, elev=30, azim=30):
    # 我们加入了新的维度 r
    r = np.exp(-(X ** 2).sum(1))
    ax = plt.subplot(projection='3d')
    ax.scatter3D(X[:, 0], X[:, 1], r, c=y, s=50, cmap='autumn')
    ax.view_init(elev=elev, azim=azim)
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_zlabel('z')



if __name__ == '__main__':
    # train_SVM()

    # fig, ax = plt.subplots(1, 2, figsize=(16, 6))
    # fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
    # for axi, N in zip(ax, [60, 120]):
    #     plot_svm(N, axi)
    #     axi.set_title('N = {0}'.format(N))

    X, y = train_svm_plus()
    plot_3D(elev=30, azim=30, X=X, y=y)
  
    

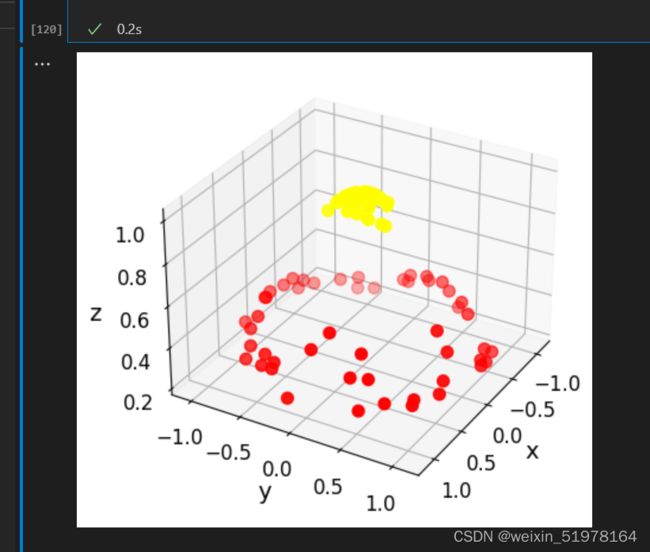
这是最后实现的三维图，用圆圈数据集造出数据集，然后实现高斯核函数升为三维，其实他就是用下面这个公式，找到那两个高斯函数对应的极值点（地标），将你像选用的那个点分别和那两个极值点进行下面公式的计算，然后比较大小，选大的，用相似度函数来替换原函数，这是一维转二维。我这次是二维转三维，也是用样的道理，同时我也发现对x,y做内积之后再做出映射和你先将x,y做出映射然后再内积是一样的结果，所以，这两者应该做法不一样，但是最后的结果应该是一样的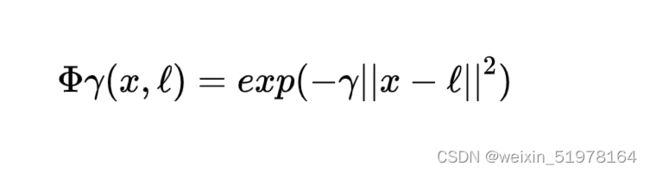

def train_svm_two():
    # 二维圆形数据 factor 内外圆比例（0， 1）
    X, y = make_circles(100, factor=0.1, noise=0.1)
     
    clf = SVC(kernel='linear')
    clf.fit(X, y)
     
    plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
    plot_SVC_decision_function(clf, plot_support=False)
    plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
                s=300, lw=1, facecolors='none')
    return X, y

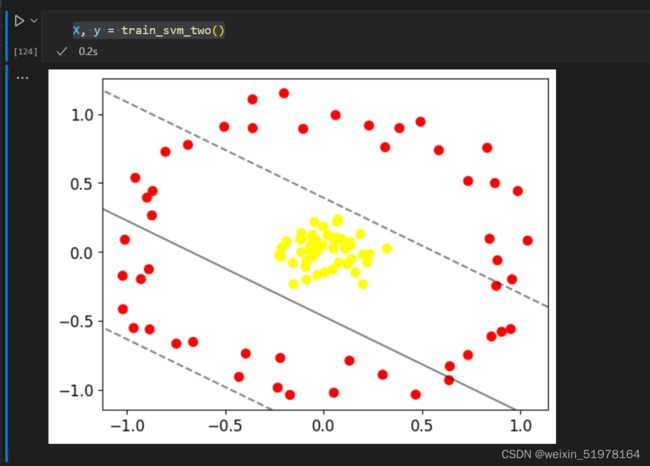
X, y = train_svm_two()

从这里就可以看出若是单单按照图上的方法那效果就不是很好，所以此时，就可以用高斯核函数。

最后选比较常见的前三种。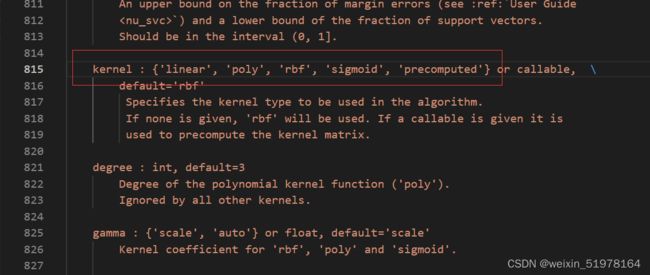

4.小结

使用核函数可以向高维空间进行映射，同时可以解决非线性的分类。SVM分类思想很简单，就是将样本与决策面的间隔最大化,同时分类效果较好。缺点也是显而易见，他对多分类比较敏感，解决比较困难，而且他也依赖于核函数的选择，以及参数的选择。所以要对参数及核函数的选择要多加实验，选择效果较好的