深度学习入门-03 实现一个简单的神经网络

1.神经网络

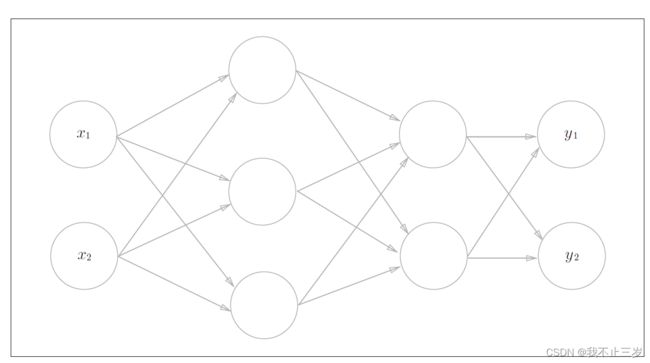
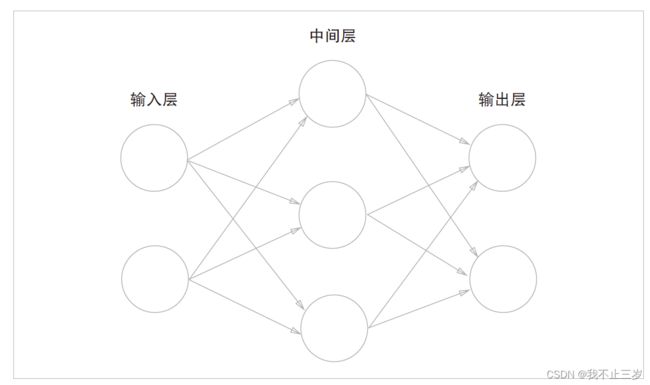
如下图，这是一个简单的神经网络框架，包含了一层输入层(两个神经元)，一层中间层(隐藏层)(三个神经元)，一层输出层(两个神经元)。因为实际包含权重的层数只有两层，所以在学习这本书的时候，下图被定义成了2层网络。有的书也定义为3层网络。

2. 激活函数

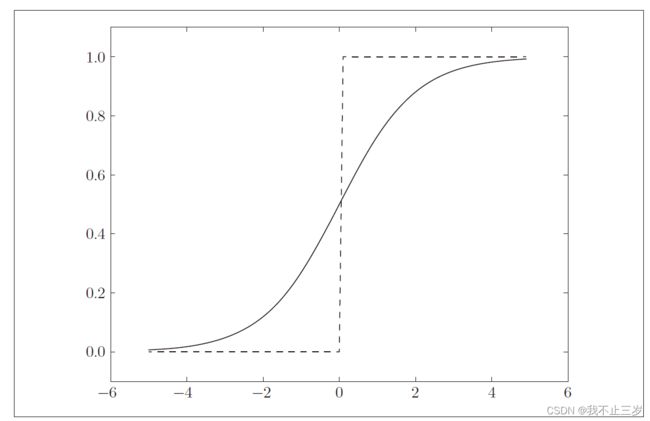
2.1sigmoid激活函数和阶跃函数对比

在前面博文中介绍过朴素感知机的相关函数，对比来看，输入层到中间层，中间层到输出层大同小异，只是输入变量，权重，偏置的矩阵维数发生了改变。但是在神经网络中我们不再使用之前的阶跃函数([前面博文用于最后转换成输出信号时使用)])，而是使用了最广为人知的sigmoid函数(在下面篇幅会介绍sigmoidoftmax,relu等区别和如何使用)。
公式如下：

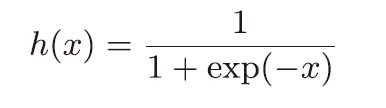
代码实现为:

def sigmoid(x):
	return 1/(1 + np.exp(-x))

sigmoid与阶跃函数对比:
上图对比:

图 阶跃函数和sigmoid函数图形对比(虚线为阶跃函数)

根据图形我们发现，
(1) sigmoid函数输出的时连续的实数值信号，而sigmoid时0或者1的二元信号，sigmoid相比较阶跃函数平滑性很好。
(2) 当输入信号为重要信息，两个函数都会输出较大值，当为不重要信息，都会输出较小的值。
(3) 无论输入信号多小或者多大，输出值都在0-1之间。
(4) 两者都是非线性函数。

2.2 激活函数为什么使用非线性的

举个例子，我们假设使用y=ax作为激活函数，无论层数有多少，链式法则嵌套多少层，都是a的n次方x乘法运算也就等价于(y=cx,其中c等于a的n次方)，还是一个线性函数，所以无法发挥多层网络优势。用了非线性函数则会随着层数增加而变得不一样，从而可以带来叠加层的优势。

2.3 另一常用激活函数-ReLU函数

sigmoid激活函数由于使用较早，现在使用最多的是ReLU函数(leakyReLU函数改进了ReLU,改进部分:当落入小于0时，梯度不更新导致"神经元死亡")。
表达公式为:

图 ReLU函数

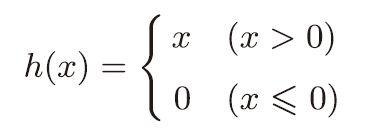
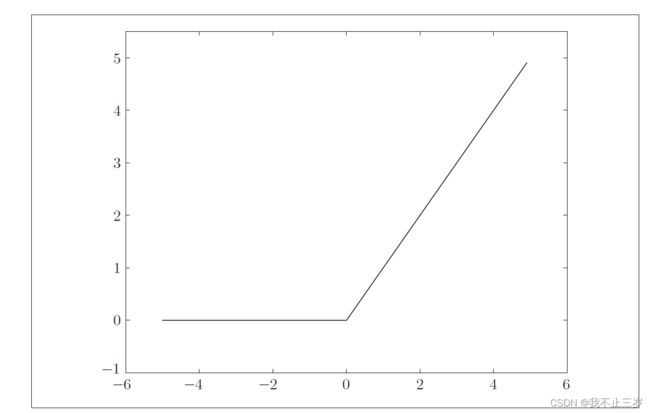
代码实现为：

def relu(x):
	return np.maximum(0,x)

根据上述我们会发现输入大于0时，会输出原值，小于等于0时，输出0. 所以relu可以在x大于0时保持梯度不衰减，从而缓解梯度消失问题。但是缺点也很明显，当训练次数达到一定程度时，部分输入就会落到小于等于0区域，导致对应权重无法更新，从而“神经元死亡” 解决方法就是leakyrelu(2.4讲解)。

题外-sigmoid与relu对比:
（1）采用sigmoid函数，计算量大(指数运算),反向传播求误差梯度时，求导设计除法，计算量相对大，而采用relu激活函数，整个过程节约计算量。
（2）sigmoid函数反向传播时,很容易就会出现梯度消失的情况，从而无法完成深度网络的训练。
（3）Relu函数会使一部分神经元输出为0，造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题。

2.4 leakyrelu函数

该激活函数改进了relu,数学表达式如下:
h(x) = max(0.1x, x)

图 leakyrelu图形 可以看出，相比于relu，在小于0时，采用的时0.1*x的形式从而避免神经元消失。

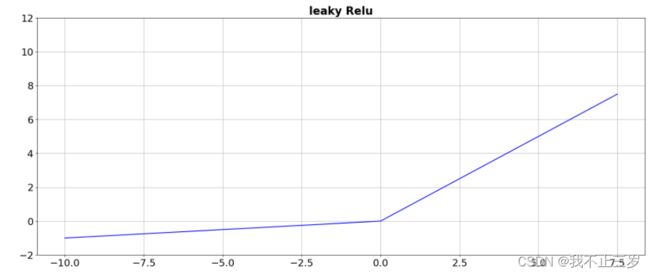
2.5 softmax函数

softmax函数用于多分类过程，是二分类函数sigmoid函数在多分类推广，目的是将多分类的结果以概率的形式展示出来。
计算公式如下:

实现代码如下:

def softmax(a):
	exp_a = np.exp(a)
	sum_exp_a = np.sum(exp_a)
	y = exp_a / sum_exp_a
	return y

softmax直白的解释就是 将网络输出的logits通过softmax函数映射到(0,1)值域空间，然后这些值累加和为1(满足概率的性质),那么我们将它理解成概率，选取概率最大(值最大)的节点，作为我们预测目标类别。

使用是的注意事项:
（1）根据softmax函数的计算公式会发现，容易造成计算机运算时的溢出现象，因此我们需要对softmax进行改进。用一下公式代替：

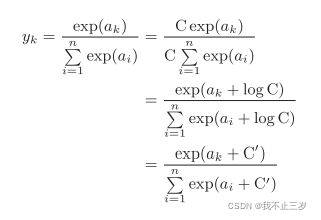
这个公式通过上下乘以一个任意常数，然后通过数学运算转成运算结果减去某个常数。以下作为示例代码进行演示:
直接计算时:

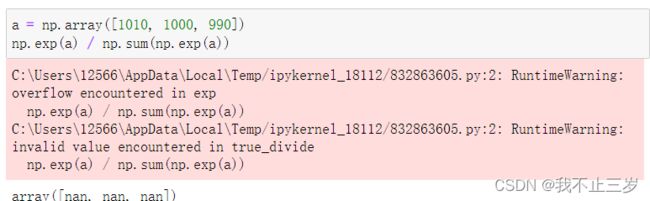
转换后计算时:

我们发现此时得到正确结果(也发现减去的常数通常是信号里的最大值)。

最后说一下softmax的特点:
(1) softmax函数输出值在0-1之间。
(2)softmax函数输出总和为1(函数输出可以解释成概率)。
(3)softmax函数不会改变各个元素之间的大小关系。

2.6 tanh函数

tanh函数是一种非常常见的激活函数，与sigmoig函数相比, 它是以0为中心，使得其收敛速度比sigmoid要快，减少迭代次数。然而，从图中可以看出，tanh两侧的导数也为0，同样会造成梯度消失。若使用时，在隐藏层使用tanh函数,输出层使用sigmoid函数。
图像如下:

图 tanh图形 根据上图中的表达公式, 代码如下:

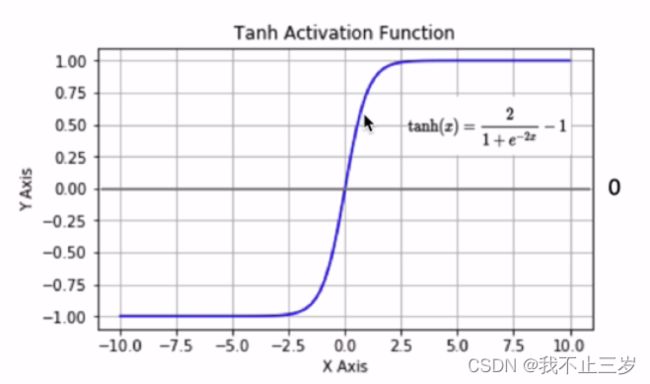
def tanh(x):
	return (2 / (1 + np.exp(-2*x)) - 1

2.7 激活函数选择

2.7.1隐藏层

对于隐藏层:
（1）优先选择ReLU激活函数
（2）如果ReLU效果不好，在尝试其他激活，如Leaky ReLU等。
（3）如果你使用了ReLU激活函数，需要注意一下神经元死亡问题，避免出现大的梯度导致过多的神经元死亡。
（4）不要使用sigmoid函数，可以尝试使用tanh激活函数

2.7.2 输出层

对于输出层:
（1）二分类问题选择sigmoid激活函数
（2）多分类问题选择softmax激活函数
（3）回归问题选择identity激活函数

三. 神经网络实现（3层）

图 三层神经网络 上图中,输入层(第0层)有两个神经元,第一个隐藏层(第一层)有3个神经元，第2个隐藏层(第2层)有2个神经元，输出层(第3层)有2个神经元

3.1 符号介绍

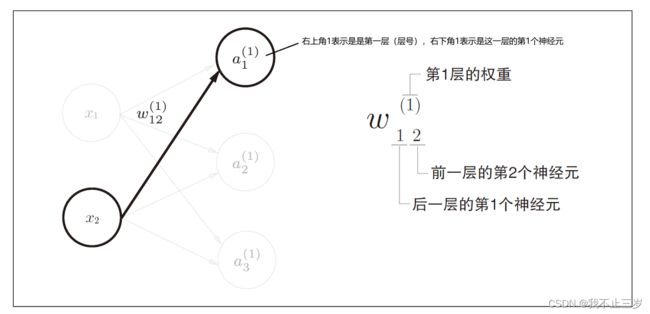
图 符号介绍

3.2 各层间的信号传递的实现

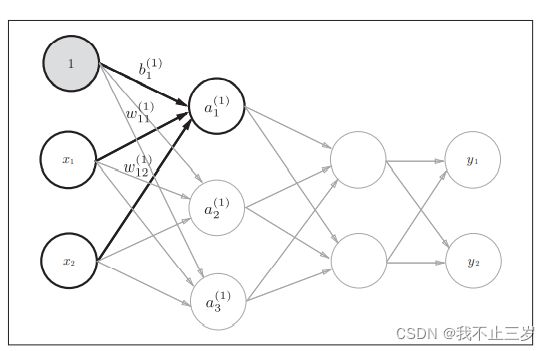
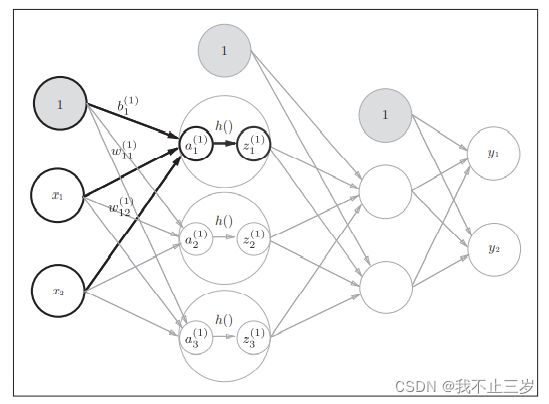
3.2.1从输入层到第一层的信号传递

图 输入层到第一层的信号传递

这一部分我们加了偏置的神经元 "1“ 右下角的索引号只有一个，因为只有一个偏置。

以隐藏层第一层的第一个神经元为例，用数学符号表示如下：

如果使用矩阵表示的话，第一层所有神经元表示如下：

其中，A,X,W,B分别表示如下：

图 第一层sigmoid函数 在进行完输入层到第一层之后，第一层需要激活函数转成输出信号Z才可以作为第一层的输出量传给第二层。

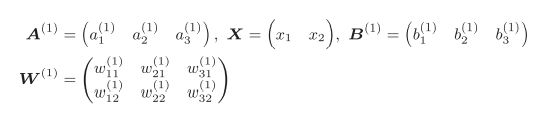
这部分用代码初始化如下(

# 初始化参数
X = np.array([1.0, 0.5])  # [2,]
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])  # [2, 3]
B1 = np.array([0.1, 0.2, 0.3])  # [3,]

# 求第一层神经元
A1 = np.dot(X, W1) + B1

# 定义sigmoid函数
def sigmoid(x):
    return 1 / ( 1 + np.exp(-x))


# 使用激活函数转换信号
Z1 = sigmoid(A1) # [3, ]
print(A1) # [0.3, 0.7, 1.1]
print(Z1)  # [0.5744452, 0.66818777, 0.75026011]

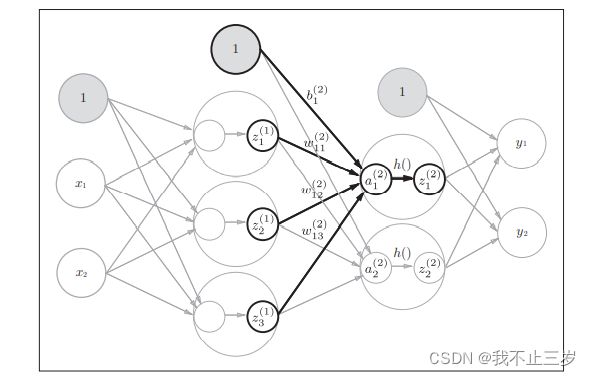
3.2.2 从第一层到第二层的传递

图 从第一层到第二层 这一部分和输入层到第一层同理，只是参数（权重和偏置）发生了变化。 这部分代码如下：

# 初始化参数
W2 = np.array([[0.1, 0.4], [0.2, 0.5]，[0.3, 0.6]])  # [3, 2]
B2 = np.array([0.1, 0.2])   # [2, ]

# 求第二层神经元
A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)

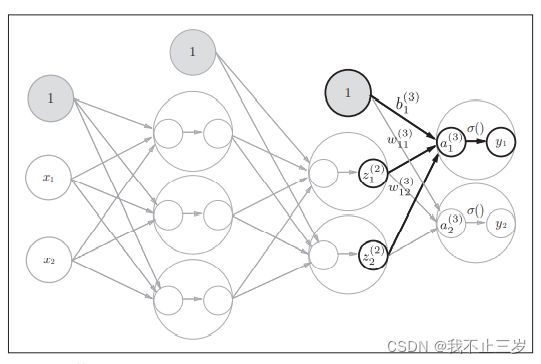
3.2.3 第2层到输出层的信号传递

图 第二层到输出层 这一部分也只介绍代码：

# 定义恒等函数(作为最后一层激活函数，具体情况下还请自主选择激活函数)
def identity_function(x):
    return x

# 初始化参数
W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])

# 求输出结果
A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3)

3.2.4 总结

到此为止，我们的三层神经网络设计完成。因为神经网络可以用于分类问题和回归问题，不过根据情况改变输出层的激活函数，一般来说，回归问题用恒等函数，分类问题用softmax函数。

四.神经网络实现方法

我们对章节3中的代码进行整理修改后代码如下:

# 定义sigmoid函数
def sigmoid(x):
    return 1 / ( 1 + np.exp(-x))

# 定义恒等函数(作为最后一层激活函数，具体情况下还请自主选择激活函数)
def identity_function(x):
    return x

# 初始化参数
def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])  
    network['b2'] = np.array([0.1, 0.2])   
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])
    return network

# 前向传播
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)
    return y
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y) # [ 0.31682708 0.69627909]

到此为止，我们实现了三层神经网络，下一节以神经网络入门案例-手写数字识别，介绍通过原生Python,Tensorflow,keras实现方法。