机器学习与深度学习个人笔记

初次接触机器学习是在19年PKU暑校，后续也断断续续有学习机器学习的知识，21年3月份加入了计算机网络实验室学习深度学习图像处理，写一篇文来记录自己的机器学习与深度学习的学习之路。

机器学习

基础理论：吴恩达机器学习课程
各个算法学习策略：博客学习+西瓜书学习+代码复现+实战

一、遗传算法（Genetic Algorithm，GA）

1.遗传算法理论

遗传算法理论学习博客

2.实战代码

代码1：遗传算法解决二元函数最值问题(原文blog，各环节解释很清晰）

图2-1 遗传算法流程图

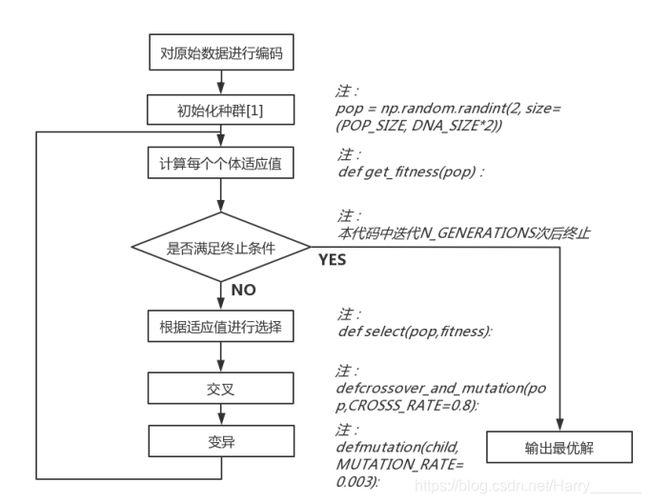
其中一些函数解释：

• np.argmax()函数
• np.random.randint(low,high,size,dtype) 作用是随机的生成介于[low,high)之间的size个数
  dtype是数据类型，默认的数据类型是np.int
• plt.ion()#将画图模式改为交互模式，程序遇到plt.show()不会暂停，而是继续执行

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

#全局变量声明，一些关键参数
DNA_SIZE=24#DNA序列长度
POP_SIZE=200#种群大小
CROSSOVER_RATE=0.8 #交叉概率
MUTATION_RATE=0.005#变异概率
N_GENERATIONS=50#遗传50代
X_BOUND=[-3,3]
Y_BOUND=[-3,3]

#要求解的二元函数
def F(x,y):
    return 3*(1-x)**2*np.exp(-(x**2)-(y+1)**2)- 10*(x/5 - x**3 - y**5)*np.exp(-x**2-y**2)- 1/3**np.exp(-(x+1)**2 - y**2)
#作3d图
def plot_3d(ax):
    X=np.linspace(*X_BOUND,100)
    Y=np.linspace(*Y_BOUND,100)
    X,Y=np.meshgrid(X,Y)
    Z=F(X,Y)
    ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap=cm.coolwarm)
    ax.set_zlim(-10,10)
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_zlabel('z')
    plt.pause(1)#实现动态绘画
    plt.show()

#解码：将二进制编码映射到区间[-3,3]上
def translateDNA(pop):#pop表示种群矩阵，一行表示一个二进制编码表示的DNA，矩阵的行数为种群数目
    x_pop=pop[:,1::2]#奇数列表示x，从索引列1开始，步长为2
    y_pop=pop[:,::2]#偶数列表示y,从索引列0开始，步长为2

    x = x_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (X_BOUND[1] - X_BOUND[0]) + X_BOUND[0]
    y = y_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (Y_BOUND[1] - Y_BOUND[0]) + Y_BOUND[0]
    return x,y

#计算适应度值:
def get_fitness(pop):
    x,y=translateDNA(pop)
    pred=F(x,y)
    return(pred-np.min(pred))+1e-3#减去最小的适应度是为了防止适应度出现负数，通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)]

#假如满足终止条件(即遗传的代数达到了N_GENERATIONS):执行下列函数：
def print_info(pop):
    fitness=get_fitness(pop)
    max_fitness_index=np.argmax(fitness)#np.argmax()通俗解释就是找数组最大值的索引
    print("max_fitness:",fitness[max_fitness_index])
    x,y=translateDNA(pop)
    print("最优的基因型：",pop[max_fitness_index])
    print("(x,y)",(x[max_fitness_index],y[max_fitness_index]))

#根据适应度值进行选择：
def select(pop,fitness):
    idx=np.random.choice(np.arange(POP_SIZE),size=POP_SIZE,replace=True,
                                    p=(fitness)/(fitness.sum()))
    return pop[idx]
#交叉与变异
def crossover_and_mutation(pop,CROSSS_RATE=0.8):
    new_pop=[]
    for father in pop:#遍历种群里的每一个个体，该个体作为父亲
        child=father #孩子先得到父亲的全部基因（01串）
        if np.random.rand()<CROSSOVER_RATE:#产生子代时不是必然发生交叉，以一定的概率发生
            mother = pop[np.random.randint(POP_SIZE)]#在种群内部随机选择一个个体作为母亲
            cross_points=np.random.randint(low=0,high=DNA_SIZE*2) #随机产生交叉的点
            child[cross_points:]=mother[cross_points]#孩子得到位于交叉点后的母亲的基因
        mutation(child)  # 每个后代有一定的机率发生变异
        new_pop.append(child)
    return new_pop
#变异
def mutation(child,MUTATION_RATE=0.003):
    if np.random.rand()<MUTATION_RATE:      #以MUTATION_RATE的概率进行变异
        mutate_point=np.random.randint(0,DNA_SIZE*2) #随机产生一个实数，代表要变异基因的位置
        child[mutate_point]=child[mutate_point]^1 #将变异点的二进制为反转

if __name__ == "__main__":
    fig = plt.figure()
    ax = Axes3D(fig)
    plt.ion()#将画图模式改为交互模式，程序遇到plt.show不会暂停，而是继续执行
    plot_3d(ax)

    pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE*2)) #matrix (POP_SIZE, DNA_SIZE)编码
    for _ in range(N_GENERATIONS):#迭代N代
        x,y = translateDNA(pop)
        if 'sca' in locals():
            sca.remove()
        sca = ax.scatter(x, y, F(x,y), c='black', marker='o')
        plt.show()
        plt.pause(0.1)
        pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))
        #F_values = F(translateDNA(pop)[0], translateDNA(pop)[1])#x, y --> Z matrix
        fitness = get_fitness(pop)
        pop = select(pop, fitness) #选择生成新的种群
    print_info(pop)
    plt.ioff()
    plot_3d(ax)

代码2：遗传算法解决TSP旅行商问题
(来自GitHubYisuZhou）

import random
import numpy as np
import math

num_city=30#城市总数0-29
num_total=100#随机生成的初始解的总数
copy_num=70#保留的解的个数
cross_num=20#交叉解的个数
var_num=10#变异解的个数

location=np.loadtxt('city_location.txt')#该文件在文末给出
#print(location)

#随机生成初始解[[],[],[]...]
def generate_initial():
    initial=[]
    city=list(range(num_city))
    for i in range(num_total):
        random.shuffle(city)
        p=city.copy()
        while (p in initial):
            #print('2333')#随机了一个重复的解
            random.shuffle(city)
            p=city.copy()
        initial.append(p)
    return initial


#对称矩阵，两个城市之间的距离
def distance_p2p_mat():
    dis_mat=[]
    for i in range(30):
        dis_mat_each=[]
        for j in range(30):
            dis=math.sqrt(pow(location[i][0]-location[j][0],2)+pow(location[i][1]-location[j][1],2))
            dis_mat_each.append(dis)
        dis_mat.append(dis_mat_each)
   # print(dis_mat)
    return dis_mat


#目标函数计算,适应度计算，中间计算。适应度为1/总距离*10000
def dis_adp_total(dis_mat,initial):
    dis_adp=[]
#    dis_test=[]   
    for i in range(num_total):
        dis=0
        for j in range(num_city-1):
            dis=dis_mat[initial[i][j]][initial[i][j+1]]+dis
        dis=dis_mat[initial[i][29]][initial[i][0]]+dis#回家
#        dis_test.append(dis)        
        dis_adp_each= 10000.0/dis
        dis_adp.append(dis_adp_each)
#    print(dis_test)
    return dis_adp




def choose_fromlast(dis_adp,answer_source):
    mid_adp=[]
    mid_adp_each=0
    for i in range(num_total):
        mid_adp_each=dis_adp[i]+mid_adp_each
        mid_adp.append(mid_adp_each)
   # print(mid_adp)
    #产生0-mid_adp[num_total-1]之间的随机数
    #选择n-1<随机数
    copy_ans=[]
    for p in range(copy_num):
        rand=random.uniform(0,mid_adp[num_total-1])#产生随机数
       # print(rand)
       # print(p)
        for j in range(num_total):
            if (rand<mid_adp[j]):#查找位置
                copy_ans.append(answer_source[j])
                break
            else:
                continue
    return copy_ans
                
    


#随机选择保留下来的70中的25个进行交叉
def cross_pronew(copy_ans):
    for i in range(cross_num):
        which=random.randint(0,copy_num-1)#选择对那个解交叉
        cross_list=copy_ans[which].copy()
        while (cross_list in copy_ans):
            p=random.randint(0,num_city-1)
            q=random.randint(0,num_city-1)
            cross_list[p],cross_list[q]=cross_list[q],cross_list[p]#第一次交换位置
            m=random.randint(0,num_city-1)
            n=random.randint(0,num_city-1)
            cross_list[m],cross_list[n]=cross_list[n],cross_list[m]#第二次交换位置            
        copy_ans.append(cross_list)
    cross_ans=copy_ans.copy()
    return cross_ans
        
    

#随机选择那95中的5个进行变异
def var_pronew(cross_ans):
    for i in range(var_num):
        which=random.randint(0,copy_num+cross_num-1)#选择对那个解交叉
        var_list=cross_ans[which].copy()
        while (var_list in cross_ans):
            p=random.randint(0,num_city-1)
            q=random.randint(0,num_city-1)
            var_list[p],var_list[q]=var_list[q],var_list[p]#交换位置
        cross_ans.append(var_list)
    var_ans=cross_ans.copy()
    return var_ans



    
'''

answer_source=generate_initial()#原initial
#print(initial)
dis_mat=distance_p2p_mat()
#print(dis_mat)
dis_adp=dis_adp_total(dis_mat,answer_source)
#print(dis_adp)
copy_answer=choose_fromlast(dis_adp,answer_source)
#print(copy_answer)
cross_answer=cross_pronew(copy_answer)
#print(cross_answer)
var_answer=var_pronew(cross_answer)
print(var_answer)



'''


answer_source=generate_initial()
dis_mat=distance_p2p_mat()
#print(dis_mat)
dis_adp=dis_adp_total(dis_mat,answer_source)
adp_max_new=max(dis_adp)
if (max(dis_adp)>10000/700):
    print('找到的最近距离是：',max(dis_adp))

else:
    print('哎呀没找到，我再找找~')    
    answer_new=answer_source
    dis_adp_new=dis_adp
    while(adp_max_new<=10000/700):
        copy_answer=choose_fromlast(dis_adp_new,answer_new)
        cross_answer=cross_pronew(copy_answer)
        var_answer=var_pronew(cross_answer)
        answer_new=var_answer.copy()
        dis_adp_new=dis_adp_total(dis_mat,answer_new)
        adp_max_new=max(dis_adp_new)
#        dis_min=10000/adp_max_new
#        print('这次是：',dis_min)


    dis_min=10000/adp_max_new
    print('终于找到你啦：',dis_min)

其中，商店坐标文件city_location.txt如下：

41 94
37 84
54 67
25 62
7 64
2 99
68 58
71 44
54 62
83 69
64 60
18 54
22 60
83 46
91 38
25 38
24 42
58 69
71 71
74 78
87 76
18 40
13 40
82 7
62 32
58 35
45 21
41 26
44 35
4 50

3.数学建模中的应用

根据我的经验，遗传算法、BP神经网络、SVM这些算法是数学建模当中最常用的智能算法。
其中，遗传算法主要用于优化问题求解或者用于对神经网络的优化当中。
小练习：

问题1
求f(x)=x 10sin(5x) 7cos(4x)的最大值，其中0<=x<=9
问题2
求下列函数的最大值
f(x)=10sin(5x)+7cos(4x) x∈[0,10]
问题3
已知n个城市之间的相互距离，现有一个推销员必须遍访这n个城市，并且每个城市只能访问一次，最后又必须返回出发城市。如何安排他对这些城市的访问次序，可使其 旅行路线的总长度最短？（设定城市共有50座，坐标可自己给定）

对于此，你感兴趣的话可以使用MATLAB或者Python根据已有的例子编写程序求解，评论区给出你的答案和问题吧~

二、粒子群算法(Particle Swarm optimization,PSO)

1.学习理论的博客

粒子群算法理论

2.算法代码

四、神经网络

1.学习理论的博客

神经网络理论CSDN
神经网络理论知乎