PyTorch框架学习十八——Layer Normalization、Instance Normalization、Group Normalization
PyTorch框架学习十八——Layer Normalization、Instance Normalization、Group Normalization
- 一、为什么要标准化?
- 二、BN、LN、IN、GN的异同
- 三、Layer Normalization
- 四、Instance Normalization
- 五、Group Normalization
上次笔记介绍了Batch Normalization以及它在PyTorch中的使用:https://blog.csdn.net/qq_40467656/article/details/108375181
这次笔记将介绍由BN引发的其他标准化层,它们各自适用于不同的应用场景,分别是适用于变长网络的Layer Normalization;适用于图像生成的Instance Normalization;适用于小mini-batch的Group Normalization。
一、为什么要标准化?
这个在上次BN的笔记中介绍过,本意是为了解决ICS问题,即随着网络层数加深,数据分布异常(很小或很大),从而导致训练困难。详情回顾:https://blog.csdn.net/qq_40467656/article/details/108375181
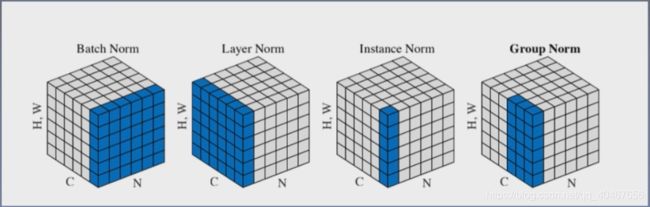
二、BN、LN、IN、GN的异同
- 同:都做了标准化的工作。
- 异:均值和方差的求取方式不一样,即选择的计算区域不一样,这个可以看完下一小节的详细介绍回过来看,可能会更能理解。
三、Layer Normalization
LN提出的起因是因为BN不适用于变长的网络,如RNN,这部分的内容还没有接触过,但是可以简单理解为这种网络的神经元个数是会变化的,不是一样的,如下图所示:
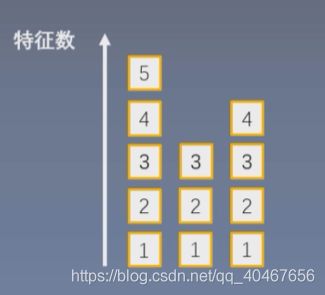
ps:注意这里的横轴不是数据样本个数,只是代表这层网络层神经元可能会变为5/3/4个,在每种个数的情况下,样本数还是一个batchsize的大小。
第一次可能有五个特征,计算得到五个均值和方差,而第二轮计算时,网络层的神经元变为3个,而BN里计算均值和方差是需要用到之前的结果的,这里之前的五个均值方差就对应不了三个特征,所以BN在这种情况下是不适用的。
那么LN是怎么计算均值和方差的呢?以一维的情况为例:
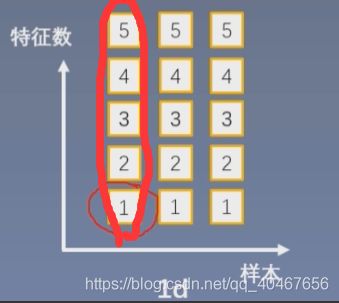
之所以称为Layer Norm,就是对该层的数据求均值和方差,不再按照特征那个维度去求,每个样本都单独求其均值方差,可以理解为逐样本的求取方式。
LN需要注意的地方:
- 不再有running_mean和running_var
- gamma和beta为逐元素的
LN在PyTorch中的实现:
torch.nn.LayerNorm(normalized_shape: Union[int, List[int], torch.Size], eps: float = 1e-05, elementwise_affine: bool = True)
- normalized_shape:(int/list/torch.Size)该层的特征维度,即要被标准化的维度。
- eps:分母修正项。
- elementwise_affine:是否需要affine transform,这里也提醒你是逐元素的仿射变换。
下面看一个PyTorch实现的例子:
import torch
import numpy as np
import torch.nn as nn
import sys, os
hello_pytorch_DIR = os.path.abspath(os.path.dirname(__file__)+os.path.sep+".."+os.path.sep+"..")
sys.path.append(hello_pytorch_DIR)
from tools.common_tools import set_seed
set_seed(1) # 设置随机种子
# ======================================== nn.layer norm
flag = 1
# flag = 0
if flag:
batch_size = 8
num_features = 3
features_shape = (3, 4)
feature_map = torch.ones(features_shape) # 2D
feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0) # 3D
feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0) # 4D
# feature_maps_bs shape is [8, 3, 3, 4], B * C * H * W
ln = nn.LayerNorm(feature_maps_bs.size()[1:], elementwise_affine=True)
# ln = nn.LayerNorm(feature_maps_bs.size()[1:], elementwise_affine=False)
# ln = nn.LayerNorm([3, 3, 4])
# ln = nn.LayerNorm([3, 3])
output = ln(feature_maps_bs)
print("Layer Normalization")
print(ln.weight.shape)
print(feature_maps_bs[0, ...])
print(output[0, ...])
结果如下:
Layer Normalization
torch.Size([3, 3, 4])
tensor([[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]],
[[2., 2., 2., 2.],
[2., 2., 2., 2.],
[2., 2., 2., 2.]],
[[3., 3., 3., 3.],
[3., 3., 3., 3.],
[3., 3., 3., 3.]]])
tensor([[[-1.2247, -1.2247, -1.2247, -1.2247],
[-1.2247, -1.2247, -1.2247, -1.2247],
[-1.2247, -1.2247, -1.2247, -1.2247]],
[[ 0.0000, 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000, 0.0000]],
[[ 1.2247, 1.2247, 1.2247, 1.2247],
[ 1.2247, 1.2247, 1.2247, 1.2247],
[ 1.2247, 1.2247, 1.2247, 1.2247]]], grad_fn=<SelectBackward>)
这边只打印了第一个数据的结果,它的均值是2,所以中间一个3×4的特征标准化之后全为0。
四、Instance Normalization
IN层的提出是因为在图像生成任务中,一个batch里的图像的风格可能不尽相同,不能通过BN的计算方式去将各个风格的特征混为一谈,所以BN在这种情况下会不适用。
那么,IN层的计算方式的思路是逐Instance(channel)地计算均值和方差,如下图所示:
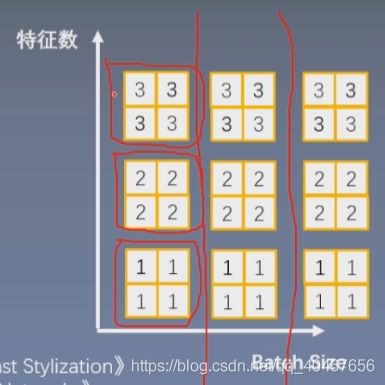
它是每一个样本每一个特征都去计算均值方差然后标准化。
IN层在PyTorch中的实现如下所示:(以二维为例)
torch.nn.InstanceNorm2d(num_features: int, eps: float = 1e-05, momentum: float = 0.1, affine: bool = False, track_running_stats: bool = False)
- num_features:一个样本特征的数量。
- eps:分母修正项。
- momentum:指数加权平均求均值方差。
- affine:是否仿射变换,默认False。
- track_running_stats:是否追踪batch,使得统计结果更具全局性,一般训练时是需要追踪,测试时不追踪,使用固定的均值方差,默认False(测试)。
看一个IN的例子:
flag = 1
# flag = 0
if flag:
batch_size = 3
num_features = 3
momentum = 0.3
features_shape = (2, 2)
feature_map = torch.ones(features_shape) # 2D
feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0) # 3D
feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0) # 4D
print("Instance Normalization")
print("input data:\n{} shape is {}".format(feature_maps_bs, feature_maps_bs.shape))
instance_n = nn.InstanceNorm2d(num_features=num_features, momentum=momentum, affine=True, track_running_stats=True)
for i in range(1):
outputs = instance_n(feature_maps_bs)
print(outputs)
print("\niter:{}, running_mean.shape: {}".format(i, instance_n.running_mean.shape))
print("iter:{}, running_var.shape: {}".format(i, instance_n.running_var.shape))
print("iter:{}, weight.shape: {}".format(i, instance_n.weight.shape))
print("iter:{}, bias.shape: {}".format(i, instance_n.bias.shape))
结果如下:
Instance Normalization
input data:
tensor([[[[1., 1.],
[1., 1.]],
[[2., 2.],
[2., 2.]],
[[3., 3.],
[3., 3.]]],
[[[1., 1.],
[1., 1.]],
[[2., 2.],
[2., 2.]],
[[3., 3.],
[3., 3.]]],
[[[1., 1.],
[1., 1.]],
[[2., 2.],
[2., 2.]],
[[3., 3.],
[3., 3.]]]]) shape is torch.Size([3, 3, 2, 2])
tensor([[[[0., 0.],
[0., 0.]],
[[0., 0.],
[0., 0.]],
[[0., 0.],
[0., 0.]]],
[[[0., 0.],
[0., 0.]],
[[0., 0.],
[0., 0.]],
[[0., 0.],
[0., 0.]]],
[[[0., 0.],
[0., 0.]],
[[0., 0.],
[0., 0.]],
[[0., 0.],
[0., 0.]]]], grad_fn=<ViewBackward>)
iter:0, running_mean.shape: torch.Size([3])
iter:0, running_var.shape: torch.Size([3])
iter:0, weight.shape: torch.Size([3])
iter:0, bias.shape: torch.Size([3])
五、Group Normalization
GN的提出是因为,随着如今数据样本变得越来越大,以现有的GPU能力可能只能放置比较小的mini-batch,而一个batch比较少的数据的话,使用BN可能计算得到的均值和方差就有较大的偏差,估计的值不准,所以BN在小mini-batch的场景下不适用。
那么GN的计算思路就是:数据样本不够,通道(特征)数来凑,其如下所示:
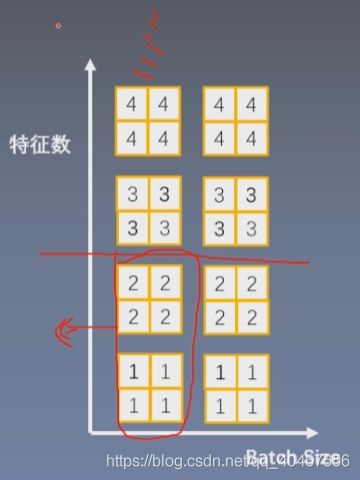
图中所示是将一个样本的两个特征划分为一个group,这里只是为了说明GN的原理,实际上特征数是很多的,比如256,那么我们分为两组的话,一组有128个特征通道,数量还是比较可观的,在这样的分组下对每一组单独求取均值方差然后标准化。
注意:
- 不再有running_mean和running_var,与LN一致。
- gamma和beta为逐通道的。
应用场景:大模型,小batch size的任务。
GN在PyTorch中的实现如下:
torch.nn.GroupNorm(num_groups: int, num_channels: int, eps: float = 1e-05, affine: bool = True)
参数如下所示:
- num_groups:分组数。
- num_channels:通道数。
- eps:同上。
- affine:是否仿射变换。
下面看一个例子:
flag = 1
# flag = 0
if flag:
batch_size = 2
num_features = 4
num_groups = 2 # 3 Expected number of channels in input to be divisible by num_groups
features_shape = (2, 2)
feature_map = torch.ones(features_shape) # 2D
feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0) # 3D
feature_maps_bs = torch.stack([feature_maps * (i + 1) for i in range(batch_size)], dim=0) # 4D
gn = nn.GroupNorm(num_groups, num_features)
outputs = gn(feature_maps_bs)
print("Group Normalization")
print(gn.weight.shape)
print(outputs[0])
结果如下:
Group Normalization
torch.Size([4])
tensor([[[-1.0000, -1.0000],
[-1.0000, -1.0000]],
[[ 1.0000, 1.0000],
[ 1.0000, 1.0000]],
[[-1.0000, -1.0000],
[-1.0000, -1.0000]],
[[ 1.0000, 1.0000],
[ 1.0000, 1.0000]]], grad_fn=<SelectBackward>)