论文精读：《DETR3D: 3D Object Detection from Multi-view Images via 3D-to-2D Queries》

DETR3D: 3D Object Detection from Multi-view Images via 3D-to-2D Queries

论文精读

摘要（Abstract）

我们介绍了一个多摄像机三维目标检测（multi-camera 3D object detection）的框架。 与现有的直接从单目图像中估计三维边界盒或利用深度预测网络从二维信息中生成用于三维目标检测的输入相比，我们的方法直接在三维空间中处理预测。

具体流程：

我们的架构从多个摄像机图像中提取2D特征，然后使用稀疏的3D对象查询集索引到这些2D特征中，使用摄像机变换矩阵将3D位置链接到多视角图像。最后，我们的模型对每个对象查询进行包围盒预测，使用集到集的损失来度量真实框和预测之间的差异。

优点：

这种自上而下的方法优于自下而上的方法，在自下而上的方法中，对象边界框预测遵循每像素深度估计，因为它不受深度预测模型引入的复合误差的影响。 而且， 该方法不需要非极大值抑制等后处理，大大提高了推理速度。

实验：

我们在Nuscenes自动驾驶基准上实现了最先进的性能。

1. 介绍（Introduction）

研究现状：

基于视觉信息的三维目标检测是低成本自动驾驶系统长期面临的挑战。 虽然利用激光雷达等方式收集的点云目标检测受益于可见目标的3D结构信息，但基于摄像机的设置更加不适定，因为我们必须仅从RGB图像中包含的2D信息生成3D包围盒预测。

现行方法[1, 2]通常纯粹从2D计算中构建他们的检测管道。 也就是说，它们使用为2D任务设计的对象检测流程（例如，CenterNet[1]、FCOS[3])来预测3D目标的位置和速度信息，而不考虑三维场景结构或传感器配置。 这些方法需要几个后处理步骤来融合跨摄像机的预测并去除冗余的检测框，从而很难在效率和有效性之间产生一个有效的权衡。

作为这些基于2D的方法的替代，一些方法通过应用三维重建方法将更多的三维计算纳入我们的目标检测流程，如[4, 5, 6]从相机图像创建伪激光雷达或场景的范围输入。 然后，他们可以将3D物体检测方法应用于这些数据，就像这些数据是直接从3D传感器收集的一样。 这种策略，无论如何，都会受到复杂错误的影响[7]: 深度估计值过低对三维目标检测的性能有很大的负面影响，它也会表现出自身的误差。

本文贡献：

在这篇论文中，我们提出了一种性能更好的的自动驾驶的二维观测和三维预测之间的转换，它不依赖于密集深度预测的模块。 我们的框架DETR3D(Multi-View 3D Detection）以自上而下的方式解决了这个问题。 通过几何反投影和摄像机变换矩阵，将二维特征提取和三维目标预测联系起来。 我们的方法从一个稀疏的对象先验集开始，在数据集中共享并端到端学习。 为了收集特定场景的信息，我们将从这些目标先验信息中解码的一组参考点反投影到每个摄像机，并获取由RESNET骨干网提取的相应图像特征8]。 从参考点的图像特征中收集的特征然后通过多头自注意力层[9]。 在一系列自注意力机制层之后，我们从每一层读取检测框参数，并使用DETR[10]来评估。
我们的体系结构不执行点云重建或从图像中显式深度预测，使其对深度估计中的误差具有鲁棒性。 此外，我们的方法不需要任何后处理，如非最大抑制(NMS)，提高效率和减少重复手工设计的方法清洗其输出。 在Nuscenes数据集上，我们的方法（不含NMS）与现有技术（含NMS）具有可比性。 在摄像机重叠区域，我们的方法明显优于其他方法。

我们将我们的主要贡献总结如下：

• 我们提出了一个流线型的RGB图像三维目标检测模型。 现有的工作在最后一个阶段结合来自不同摄像机视图的目标预测，而我们的方法融合了来自每一层计算的所有摄像机视图的信息。 据我们所知，这是首次尝试将多摄像机检测作为三维集对集预测（3D set-to-set prediction）。
• 我们引入了一个模块，通过向后几何投影（backward geometric projection）连接二维特征提取和三维包围盒预测。 它不会受到来自二级网络的不准确深度预测的影响，并通过将3D信息反投影到所有可用帧上来, 无缝地使用来自多个相机的信息。
• 类似于对象DGCNN[11]我们的方法不需要像每幅图像或全局NMS这样的后处理，它与现有的基于NMS的方法不相上下。 在相机重叠区域，我们的方法比其他方法有很大的优势。

2. 相关工作（Related work）

• 2D object detection
• Set-based object detection
• Monocular 3D object detection

3. 多视角3D目标检测（Multi-view 3D Object Detection）

3.1 综述（Overview）

我们的模型结构输入从一组已知投影矩阵（内参和相关外因的组合）的摄像机收集的RGB图像，并输出场景中对象的一组3D包围盒参数。 与过去的方法不同，我们基于一些高层需求，构建我们的体系结构：

• 我们将3D信息合并到我们模型结构中的中间计算中，而不是在图像平面中执行纯粹的2D计算。
• 我们不估计密集的三维场景几何，避免了相关的重建误差。
• 我们避免了像NMS这样的后处理步骤。

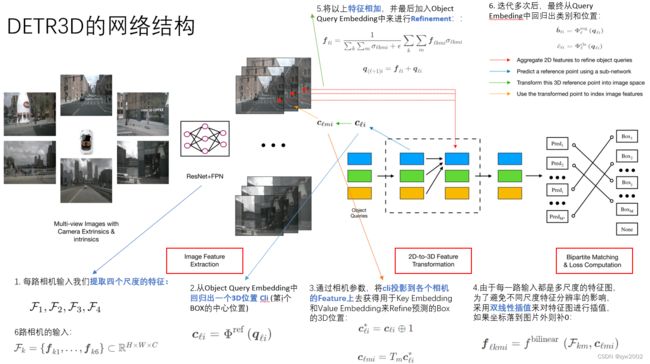
我们使用一个新的集合预测模块来解决这些问题，该模块通过在二维和三维计算之间交替来连接二维特征提取和三维框预测。 我们的模型包含三个关键组件，如图1所示，首先，遵循2D视觉中的常见做法，它使用一个共享的ResNet主干网络。 可选地，这些特征由特征金字塔网络(FPN)增强 。 第二，检测头–我们的主要贡献–以几何感知的方式将计算出的2D特征链接到一组3D预测包围盒。 检测头的每一层都从稀疏的对象查询集开始，这些对象查询是从数据中学习的。 每个对象查询编码一个3D位置，该位置投影到摄像机平面上，通过双线性插值来收集图像特征。 和 DETR类似，然后我们使用多头注意力通过合并对象交互来细化对象查询。 这一层重复多次，在特征采样和对象查询细化之间交替进行。 最后，我们评估了一个集到集的损失的训练网络。

我们方法的概述: 该模型的输入是一组多视图图像，这些图像由RESNet和FPN编码。 然后，我们的模型对一组稀疏对象查询进行操作，其中每个查询都被解码到一个3D参考点。 通过将三维参考点投影到图像空间中，对二维特征进行变换，以细化目标查询。 我们的模型对每个查询进行预测，并使用集对集的损失。

3.2 特征学习（Feature Learning）

我们的模型从一组由周围摄像头捕捉的图片$\mathcal{I}=\left\{\mathbf{i}\mathbf{m}1,\dots ,\mathbf{i}\mathbf{m}K\right\}\subset {\mathbb{R}}^{\mathrm{H}\mathrm{i}\mathrm{m}\times \mathrm{W}\mathrm{i}\mathrm{m}\times 3}$ 开始。相机矩阵$\mathcal{T}=\left\{T_1,\dots ,T_K\right\}\subset {\mathbb{R}}^{3\times 4}$, 真实检测框$\mathcal{B}=\left\{{\mathbf{b}}_1,\dots ,{\mathbf{b}}_j,\dots ,{\mathbf{b}}_M\right\}\subset {\mathbb{R}}^9$, 和类别标签$\mathcal{C}=\left\{c_1,\dots ,c_j,\dots ,c_M\right\}\subset \mathbb{Z}$. 每一个${\mathbf{b}}_j$ 包含在BEV视图中的位置、大小、尺寸、偏向角、速度。 我们的模型旨在从这些图像中预测这些检测框和它们的标签。我们不使用点云，点云通常由高端激光雷达捕获。这些图像通过ResNet 和 FPN网络编码成4组特征${\mathcal{F}}_1,{\mathcal{F}}_2,{\mathcal{F}}_3,\mathcal{F}4$ , 每个集合$\mathcal{F}k=\left\{\mathbf{f}k1,\dots ,\mathbf{f}k6\right\}\subset {\mathbb{R}}^{H\times W\times C}$对应6幅图像的某一层次特征。 这些多尺度特征为识别不同大小的物体提供了丰富的信息。接下来，我们将详细介绍使用一个新的集合预测模块将这些2D特征转换为3D的方法。

3.3 检测头（Detection Head）

现有的从摄像机输入中检测目标的方法通常采用自底向上的方法，该方法预测每个图像的稠密的包围盒集，过滤图像之间的冗余盒，并在后处理步骤中聚合跨摄像机的预测。 这种范式有两个至关重要的缺点：密集包围盒预测需要精确的深度感知，这本身就是一个具有挑战性的问题； 而基于NMS的冗余去除和聚合是不可并行化的操作，引入了很大的推理开销。 我们使用下面描述的自上而下的对象检测头来解决这些问题。

DETR3D是迭代的，它使用$L$层和基于集合的计算，从2D特征映射产生包围盒估计。 每一层都包括以下步骤：

1. 预测与对象查询相关联的一组检测框中心。
2. 利用摄像机变换矩阵将这些中心投影到所有的特征图中。
3. 通过双线性插值对特征进行采样，并将其合并到对象查询中。
4. 使用多头注意力描述对象交互。

受DETR的启发, 每一层$\ell \in \{0,\dots ,L-1\}$ 作用于一组目标查询：${\mathcal{Q}}_{\ell }=\left\{{\mathbf{q}}_{\ell 1},\dots ,{\mathbf{q}}_{\ell M^{\ast }}\right\}\subset {\mathbb{R}}^C$, 生成一组新的集合${\mathcal{Q}}_{\ell +1}$. 一个参考点${\mathbf{c}}_{\ell i}\in {\mathbb{R}}^3$从一个目标查询${\mathbf{q}}_{\ell i}$中解码出来

$${\mathbf{c}}_{\ell i}={\Phi }^{\mathrm{r}\mathrm{e}\mathrm{f}}\left({\mathbf{q}}_{\ell i}\right)$$

其中${\Phi }^{\text{ref }}$ 是神经网络。 ${\mathbf{c}}_{\ell i}$ 可以被认为是假设的第$i$个盒子中心。 然后我们依据$c\ell i$来获取图像特征，并进一步进行微调和预测检测框。然后，$\mathbf{c}\ell i$ (或者更准确地说，它的齐次对应物${\mathbf{c}}_{\ell i}$ ) 通过相机的转换参数被投影到每一张图片中。

$${\mathbf{c}}_{\ell i}^{\ast }={\mathbf{c}}_{\ell i}\oplus 1{\mathbf{c}}_{\ell mi}=T_m{\mathbf{c}}_{\ell i}^{\ast },$$

其中，$\oplus$ 表示连接， 然后 ${\mathbf{c}}_{\ell mi}$ 是参考点到第$m$个相机的投影。 为了消除特征图大小的影响并跨不同级别收集特征。我们把${\mathbf{c}}_{\ell mi}$ 规范话到$[-1,1]$.接下来，通过以下步骤收集图像特征:

$${\mathbf{f}}_{\ell kmi}=f^{\text{bilinear }}\left({\mathcal{F}}_{km},{\mathbf{c}}_{\ell mi}\right)$$

其中${\mathbf{f}}_{\ell kmi}$ 是在$\ell$ 层 第$k$个级别第$m$个相机中的第$i$个点。给定的参考点不一定在所有的摄像机图像中都可见，因此需要一些启发式算法来过滤无效点。 为此，我们定义了一个二进制值${\sigma }_{\ell kmi}$, 它是基于参考点是否被投影到图像平面之外来确定的。
最终的特征$f_{\ell i}$ 以及在下一层的目标查询${\mathbf{q}}_{(\ell +1)i}$ 由下式给出 :

${\mathbf{f}}_{\ell i}=\frac{1}{{\sum }_k{\sum }_m{\sigma }_{\ell kmi}+ϵ}{\sum }_k{\sum }_m{\mathbf{f}}_{\ell kmi}{\sigma }_{\ell kmi}\text{ and }{\mathbf{q}}_{(\ell +1)i}={\mathbf{f}}_{\ell i}+{\mathbf{q}}_{\ell i}$

其中$ϵ$ 是一个小数，避免被零除。最后，对于每个对象查询${\mathbf{q}}_{\ell i}$, 我们预测一个检测框${\hat{\mathbf{b}}}_{\ell i}$ 和一个类别标签${\hat{c}}_{\ell i}$ 和两个神经网络$\Phi {\ell }^{\text{reg }}$ 和${\Phi }_{\ell }^{\mathrm{c}\mathrm{l}\mathrm{s}}$ :

$${\hat{\mathbf{b}}}_{\ell i}=\Phi {\ell }^{\mathrm{r}\mathrm{e}\mathrm{g}}\left({\mathbf{q}}_{\ell i}\right)\text{ and }\hat{c}\ell i={\Phi }_{\ell }^{\mathrm{c}\mathrm{l}\mathrm{s}}\left({\mathbf{q}}_{\ell i}\right).$$

我们在训练中从每一层计算预测的损失${\hat{\mathcal{B}}}_{\ell }=\left\{{\hat{\mathbf{b}}}_{\ell 1},\dots ,{\hat{\mathbf{b}}}_{\ell j},\dots ,{\hat{\mathbf{b}}}_{\ell M^{\ast }}\right\}\subset {\mathbb{R}}^9$和${\hat{\mathcal{C}}}_{\ell }=\left\{{\hat{c}}_{\ell 1},\dots ,{\hat{c}}_{\ell j},\dots ,{\hat{c}}_{\ell M}\right\}\subset \mathbb{Z}$。 在推理过程中，我们只使用最后一层的输出。

3.4 损失（Loss）

我们采用集合到集合的损失来计算预测集合$\left(\hat{\mathcal{B}}\ell ,\hat{\mathcal{C}}\ell \right)$和真实集合$(\mathcal{B},\mathcal{C})$之间的差异。这个损失由两个部分组成：对于类别标签的focal loss，对于检测框参数的$L^{1}Loss$ 。 为了记号上的方便，我们把$\hat{\mathcal{B}}\ell$和$\hat{\mathcal{C}}\ell$中的下标$\ell$去掉。真实框的数量$M$ 通常小于预测的数量$M^{\ast }$。 因此，为了方便计算，我们将真实框集合中添加了$\varnothing$s (无对象)， 最多为$M^{\ast }$个。 我们通过二部匹配问题（bipartite matching problem）建立了基本真值和预测值之间的对应关系： ${\sigma }^{=}\arg \min \sigma \in \mathcal{P}\sum {j=1}^M-1_{\left\{c_j\ne \varnothing \right\}}\hat{p}\sigma (j)\left(c_j\right)+1\left\{c_j=\varnothing \right\}\mathcal{L}\text{box }\left(\mathbf{b}j,\hat{\mathbf{b}}\sigma (j)\right)$

其中$\mathcal{P}$表示排列的组合, $\hat{p}\sigma (j)\left(c_j\right)$ 是对于编号为$\sigma (j)$ 的预测类别是$c_j$的概率。 $\mathcal{L}\text{box }$ 是对于检测框参数的$L_1$损失。 我们使用匈牙利算法解这个赋值问题, 产生集合到集合的损失:

$$\mathcal{L}\text{sup }=\sum _{j=1}^N-\log {\hat{p}}_{{\sigma }^{(}j)}\left(c_j\right)+1_{\left\{c_j=\varnothing \right\}}{\mathcal{L}}_{\text{box }}\left(\mathbf{b}j,\hat{\mathbf{b}}{\sigma }^{\ast }(j)\right)$$