主成分分析和协方差矩阵
文章目录
- 前言
- 理论分析
-
- (一).构建线性空间
- (二).实现最近重构性
- (三).实现最大可分性
- (四).最大化协方差矩阵
- (五).Numpy库实现主成分分析
前言
本文主要介绍机器学习中的无监督学习数据降维方法:主成分分析法。主成分分析法是一种无监督学习的线性变换技术,用于数据的特征提取和降维。本文主要介绍主成分分析的相关理论,并三种方法实现主成分分析:分别是通过scikit-learn库实现主成分分析,numpy库实现主成分分析以及通过spss软件实现主成分分析。
理论分析
理解好理论的推导需要一定的数学知识基础,我在这里罗列下来:
- 线性空间理论
- 协方差矩阵
- 拉格朗日乘子法
(一).构建线性空间
我们提到主成分分析是一种降维的方法,所谓降维就是把很多个随机变量降到我们想要的低维度。我们进行数据分析时,往往得到很多个随机变量(也就是影响因变量 y y y的因素: X 1 , X 2 , . . . X n X_1,X_2,...X_n X1,X2,...Xn),根据线性空间理论我们可以认为这 n n n个随机变量代表 n n n维空间中的 n n n个维度,而因变量 y y y则作为这 n n n个‘坐标’所确定的‘点’。
这里的说明比较抽象,但是我们可以类比我们常见的三维空间(笛卡尔坐标系),我们通过三个坐标确定了一个点,由于点和向量是一一对应的,也是说三个坐标确定了一个三维向量。以此类推, n n n维空间中, n n n个坐标确定了一个 n n n维向量(这里的 n n n维向量不再是我们一般的有向线段,而是一个抽象的数学量)。如果拿影响房价的100多个因素来举例,那么这100多个因素就是我们这个线性空间中的坐标,而房价就是这100多个坐标确定的向量(或者理解为‘点’,因为二者一一对应)。
(二).实现最近重构性
上面我们构建了线性空间的模型。我们提到主成分分析法是用于数据的降维,那么如何理解这个降维概念?
我们可以想象下二维的情形,通过两个坐标确定一个点。如果我们想要把二维降维降到一维,我们可是引出一条直线,只要我们算出点到直线的距离就可以确定所有的点(如下图所示,这里是借用吴恩达老师课程中图片),也就通过一个变量确定样本点。三维的类似,可以通过一个二维平面确定。对于更高维的空间,则需要一个“超平面”(平面的推广)来确定所有的点。
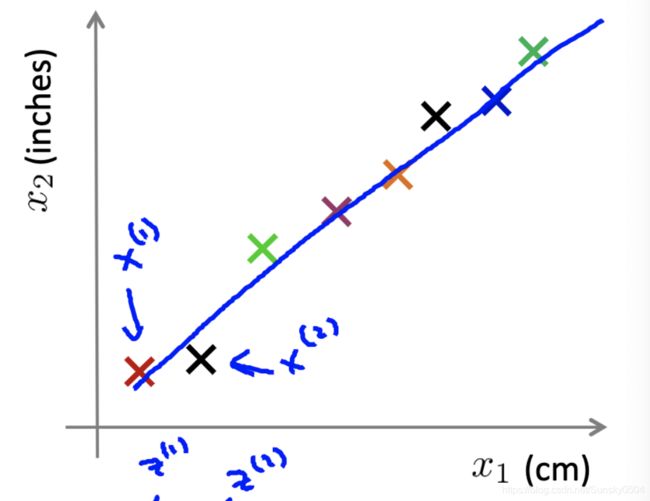
那么如何找到这个超平面?我们还是从二维,三维出发去理解。上面说的我们可以通过线和面代替二维和三维空间,那么选定的这些线和面要满足什么条件?
第一点:尽可能的让我们的点(样本点)都落在这个线或者面上,原因是如果我们的样本点都完全落在了线或面上,我们就完全的可以用线或面来表示所有的样本,这样二维平面完全可以用坐标轴(一根线)来替代,三维空间完全可以用二维平面来替代。但是这是理想情况,实际很难实现,为方便起见,我们定义一个量来表达我们样本空间中的所有的点(原样本点)和低维空间中的样本点(投影重构的点)之间的距离。
为了推出这个表达式,我们先对一些量进行说明:
- 样本空间中一共有 m m m个向量(即 m m m个样本点),第 i i i个记为: x i \bm{x_i} xi;
- 降维之后的低维空间的维度为 d ′ d' d′,其标准正交基向量为: { w 1 , w 2 , w 3 . . . w d ′ } \bm{\{w_1,w_2,w_3...w_{d'}\}} {w1,w2,w3...wd′}
- 原样本空间中的向量: x i \bm{x_i} xi在低维空间中坐标表达式为: z i = ( z i 1 , z i 2 , . . . z i d ′ ) \bm{z_i}=(z_{i1},z_{i2},...z_{id'}) zi=(zi1,zi2,...zid′); 向量表达式为:
z i = ∑ j = 1 d ′ z i j w j \bm{z_i}=\displaystyle\sum_{j=1}^{d'} z_{ij}\bm{w_j} zi=j=1∑d′zijwj - 原样本空间的样本点 x i \bm{x_i} xi和降维之后的 z i \bm{z_i} zi之间的距离为: ∥ ∑ j = 1 d ′ z i j w j − x i ∥ 2 2 _\|\displaystyle\sum_{j=1}^{d'} z_{ij}\bm{w_j}-\bm{{x_i}}\|^2_2 ∥j=1∑d′zijwj−xi∥22
基于以上的变量说明,我们可以得到原本空间中的所有的点(原样本点)和低维空间中的样本点(投影重构的点)之间的距离: ∑ i = 1 m ∥ ∑ j = 1 d ′ z i j w j − x i ∥ 2 2 ∝ − t r ( W T ∑ i = 1 m x i x i T W ) \displaystyle\sum_{i=1}^m \\_\|\displaystyle\sum_{j=1}^{d'} z_{ij}\bm{w_j}-\bm{{x_i}}\|^2_2∝-tr(\bm{W^T}\displaystyle\sum_{i=1}^m \bm{x_i} \bm{x_i^T}\bm{W}) i=1∑m∥j=1∑d′zijwj−xi∥22∝−tr(WTi=1∑mxixiTW)
其中:
∑ i = 1 m x i x i T \displaystyle\sum_{i=1}^m \bm{x_i} \bm{x_i^T} i=1∑mxixiT为投影之后样本点的协方差矩阵,
W = ( w 1 , w 2 , w 3 . . . w d ′ ) \bm{W}=\bm{(w_1,w_2,w_3...w_{d'})} W=(w1,w2,w3...wd′)
为低维空间的标准正交基向量。
此时我们已经得到了原本空间中的所有的点(原样本点)和低维空间中的样本点(投影重构的点)之间的距离的表达式,按照我们之前的分析我们选取的维度应尽可能让这个距离小,也就是让 W T ∑ i = 1 m x i x i T W = W T X X T W \bm{W^T}\displaystyle\sum_{i=1}^m \bm{x_i} \bm{x_i^T}\bm{W}=\bm{W^T}\bm{X} \bm{X^T}\bm{W} WTi=1∑mxixiTW=WTXXTW量变大,如何变大,我们一会儿在后面分析。
(三).实现最大可分性
上面说到我们选取的低维空间应尽可能的实现原空间的样本点和投影之后的样本点距离最小化,但是仅仅满足这个距离最小化还是不足以满足我们所要寻找的平面的条件,为什么呢?
虽然我们实现了距离的最小化,但是如果就是我们在低维空间中的投影点都重合到了一起,也就是原样本空间中 m m m个样本点在低维空间中都集中在了一个点,我们就无法分辨这样投影之后的样本点,这其实就违背了我们最初的目的,即违背了实现对高维空间的样本点的在低维空间恰当的表达。
第二点:尽可能使在低维空间投影后的样本点的分开。考虑到协方差矩阵,协方差矩阵代表着样本点的方差(随机变量自身的离散程度)和协方差(随机变量的关系),所以我们要实现协方差矩阵的最大化。即:
m a x : W T ∑ i = 1 m x i x i T W = W T X X T W max:\bm{W^T}\displaystyle\sum_{i=1}^m \bm{x_i} \bm{x_i^T}\bm{W}=\bm{W^T}\bm{X} \bm{X^T}\bm{W} max:WTi=1∑mxixiTW=WTXXTW
(四).最大化协方差矩阵
上面我们分析了实现降维的平面要满足的两个条件:最近重构性和最大可分性。有趣的是要实现这两个条件我们只需要是样本点在低维空间的协方差矩阵最大化即可,也就是说我们只需要最大化样本点在低维空间中的协方差矩阵,由此可见协方差矩阵的重要性!那么如何最大化样本点在低维空间中的协方差矩阵( W T X X T W \bm{W^T}\bm{X} \bm{X^T}\bm{W} WTXXTW)?
这里我们不具体推导,简单的介绍下思路。最大化协方差矩阵其实是一个极值问题,我们通常借助拉格朗日乘子法(可以参考高等数学同济版下册多元函数的条件极值问题)解决这样的问题。
将协方差矩阵写成带乘子的形式:
X X T w i = λ i w i \bm{X} \bm{X^T}\bm{w_i}=\bm{\lambda_iw_i} XXTwi=λiwi
( W T W = I ) (\bm{W^T\bm{W}=\bm{I}}) (WTW=I)
在低维空间的每个维度都求解这样的方程,得到 d d d个维度下的 λ i ( i = 1 , 2 , . . . d ) \lambda_i(i=1,2,...d) λi(i=1,2,...d)取值, λ i \lambda_i λi的大小就代表我们在低维空间中样本点在 i i i方向上的方差或者说是离散程度,根据前面的要求:选取满足最近重构性和最大可分性的维度,所以就可以根据 λ i \lambda_i λi的大小进行选取。
补充(可以跳过):
1.我们求解上面的方程,其实是一个本征(特征)值问题,本征值(特征值)是 λ i \lambda_i λi,本征(特征)向量是 w i \bm{w_i} wi, 本征(特征)矩阵是 X X T \bm{X} \bm{X^T} XXT
2.更深入的理解可以参考:What is the Covariance Matrix?
(五).Numpy库实现主成分分析
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
#读取数据集
df = pd.read_csv("wine.data")
X = df.iloc[:,1:]
y = df.iloc[:,0]
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,stratify=y,random_state=0)
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)
#获得协方差矩阵
covriance_matrix = np.cov(X_train_std.T)
#获得特征值和特征向量
eigen_vals ,eigen_vecs = np.linalg.eig(covriance_matrix)
#输出结果如如下:
array([4.79500219, 2.50003078, 1.44306678, 0.99901271, 0.87517717,
0.67821564, 0.53031813, 0.35080209, 0.28446498, 0.11333093,
0.14810971, 0.18968162, 0.19934466])
数据集在我的Github上,另有关于吴恩达老师的课程资料pdf。
- 关于sc.fit_transform()的说明
from sklearn.preprocessing import StandardScaler
import numpy as np
X_train = np.array([[ 1., -1., 2.],
[ 2., 0., 0.],
[ 0., 1., -1.]])
scaler = StandardScaler().fit(X_train)
#获得样本数据的每个维度的均值
scaler.mean_
#输出结果为:
array([1. , 0. , 0.33333333])
#获得样本数据的每个维度的标准差
scaler.scale_
#输出结果为:
array([0.81649658, 0.81649658, 1.24721913])
#获得样本数据的每个维度的方差
scaler.var_
#输出结果为:
array([0.66666667, 0.66666667, 1.55555556])
#将方差开根号和标准差对比,二者相等
np.sqrt(scaler.var_)
#输出结果为:
array([0.81649658, 0.81649658, 1.24721913])
- 关于sc.transform()的说明:传入数据,按照sc.fit_transform()获得均值和标准差对数据进行标准化处理;