spss进行主成分分析
什么是主成分分析
简而概之, 就是一组数据受太多因素影响, 选出几个能代表他们的因素,并进行线性组合得到一组比原维度小的因素组合, 作为新的因素集
用spss操作
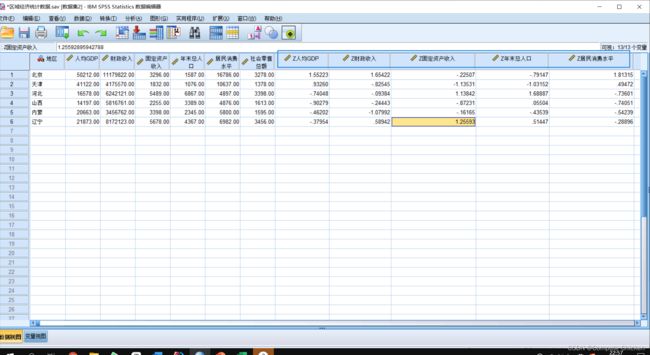
随手拿出一组数据
1.数据统一标准化
因为我们得到的原始数据大小,类型不一, 一起分析会不准确, 所以将数据全部标准化到[-10,10]的范围内
选择 分析--描述统计--描述
将变量都放入右侧, 并选中将标准化值另存为变量,点击确定
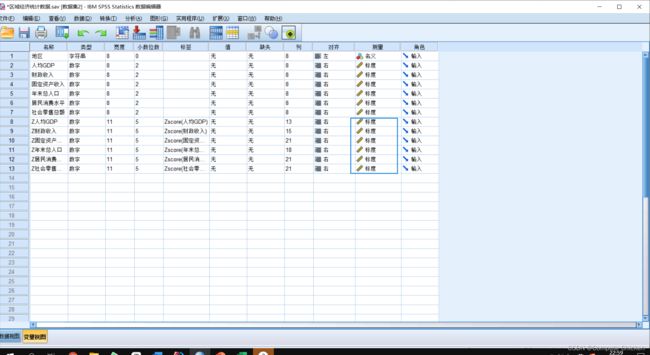
后面以Z开头的都是各变量标准化之后的值, 可以发现所有的变量都在[-10, 10]范围内
记得修改标准化值的类型和原值一样(我的全是标量)
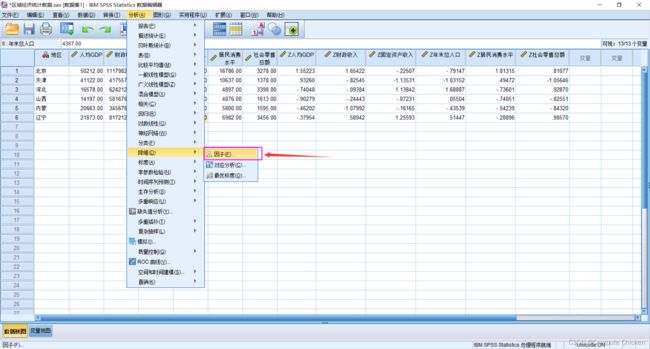
进行因子分析
选择 分析--降维--因子分析
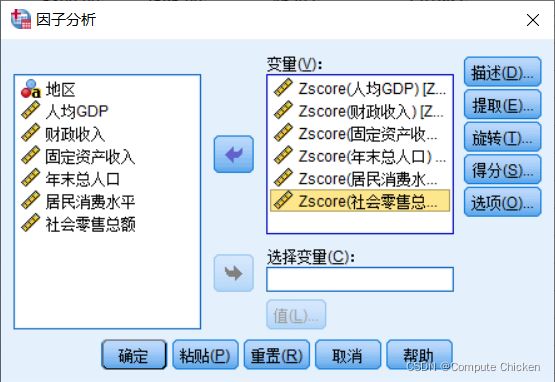
将标准化之后的值全部选中,原始值不要选
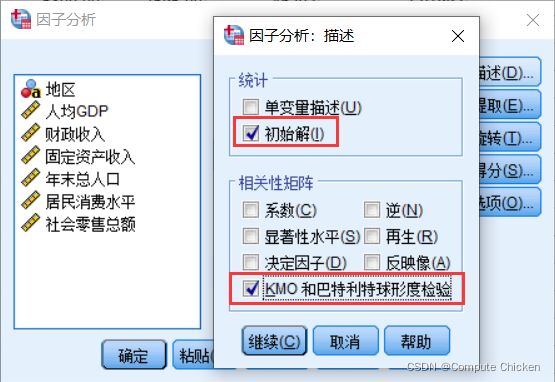
描述: 选中 初始解和KMO和巴特利特球形度检验
提取: 选择 协方差矩阵和碎石图
得分: 选择保存为变量
其他的选项默认就好, 然后点击确定
主要关注 总方差解释, 可以发现前两个变量就占了94%多的影响度(一般占到85%以上就可以通过), 所以完全可以用前两个变量代替其他的变量
这个结果也可以通过碎石图直观地表示:
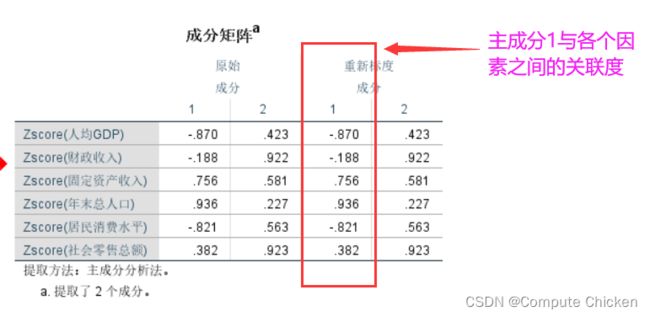
成分矩阵表示 各个主成分与各个因素之间的关系有多大
将成分矩阵的重新标度成分, 复制粘贴到变量中, 变成一个新变量,分别记为V1, V2
转换得到主成分分析的系数
因为spss中只有因子分析, 所以还需要对因子分析的系数做处理才能得到主成分分析的系数(建议先了解主成分分析和因子分析的关系, 我是看的b站数模老哥的视频23节)
它们之间的关系是 因子分析的系数 / sqrt(特征值) = 主成分分析的系数
特征值就是总方差解释中的总计
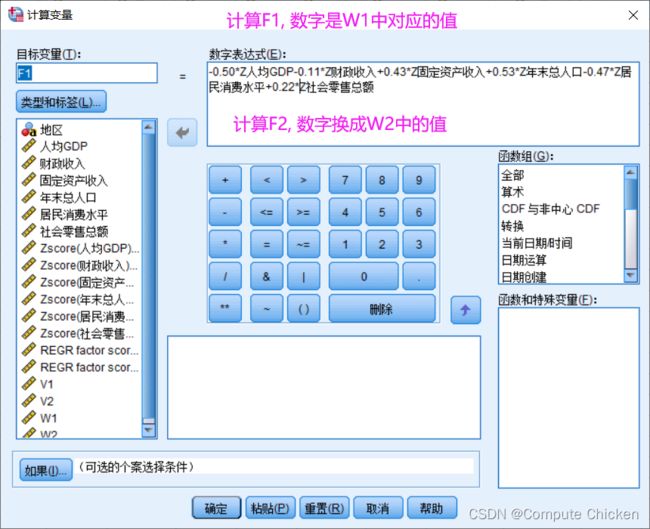
然后在 转换--计算变量中可以进行相关计算
计算过程类似于excel, 就不多说了,直接上公式
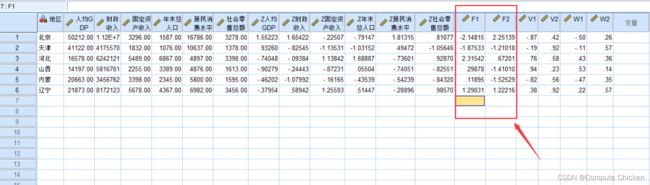
然后再把 主成分分析的系数与原始值标准化之后的值对应相乘, 分别得到最终结果F1, F2
也是在 转换--计算变量 中计算
最后, 6个因素降维成只剩下F1, F2两个因素了, 处理问题简化了很多