机器学习笔记-牛顿法
牛顿法
文章目录
- 牛顿法
- 一、梯度下降法的缺点
- 二、牛顿法优化原理
- 三、算法实现
- 总结
一、梯度下降法的缺点
上篇博客介绍了梯度下降法的原理,但是没有详细介绍梯度下降法的下降趋势的缺点,这里打算先介绍一下梯度下降法在迭代过程中会出现的情况。
上次介绍梯度下降法在优化过程中接近极小值点 x ‾ \overline x x 时,每次的迭代移动步长会很小,会出现锯齿现象,导致所用的时间大大加大。造成这样的原因就是用梯度下降法极小化目标函数时,相邻两个搜索方向是正交的。
如果我们设
φ ( x ) = f ( x ( k ) + λ d ( k ) ) \varphi (x) = f({x^{(k)}} + \lambda {d^{(k)}}) φ(x)=f(x(k)+λd(k))
d ( k ) = − ∇ f ( x ( k ) ) {d^{(k)}} = - \nabla f({x^{(k)}}) d(k)=−∇f(x(k))
为求出从 x ( k ) {x^{(k)}} x(k)出发沿方向 d ( k ) {d^{(k)}} d(k)的极小值点,
φ ′ ( λ ) = ∇ f ( x ( k ) + λ k d ( k ) ) T d ( k ) = 0 {\varphi ^{'}}(\lambda ) = \nabla f{({x^{(k)}} + {\lambda _k}{d^{(k)}})^T}{d^{(k)}} = 0 φ′(λ)=∇f(x(k)+λkd(k))Td(k)=0
就可以得出:
− ∇ f ( x ( k + 1 ) ) T ∇ f ( x ( k ) ) = 0 - \nabla f{({x^{(k + 1)}})^T}\nabla f({x^{(k)}}) = 0 −∇f(x(k+1))T∇f(x(k))=0
即方向 d ( k + 1 ) = − ∇ f ( x ( k + 1 ) ) {d^{(k + 1)}} = - \nabla f({x^{(k + 1)}}) d(k+1)=−∇f(x(k+1))与 d ( k ) = − ∇ f ( x ( k ) ) {d^{(k)}} = - \nabla f({x^{(k)}}) d(k)=−∇f(x(k))正交,这也说明迭代产生的序列{ x ( k ) {x^{(k)}} x(k)}所走路径是“之”字型的。
就会出现下面的迭代图像

具体更详细的介绍可以参考《最优化理论与算法》这本书,梯度下降法反映了目标函数的一种局部性质。从局部来看,梯度下降法方向确实是函数值下降最快的方向,选择这样的方向进行搜索是有利的,但从全局来看,受到锯齿因素的影响,即使向着极小值移动不太大的距离,也要经历不少的弯路,因此使收敛速率大为减慢,梯度下降法并不是收敛最快的方法,相反,从全局看,它的收敛是比较慢的,因此,最速下降法一般适用于计算过程的前期迭代或作为间插步骤,当接近极小值点时,再使用梯度下降法,其实不是一个很好的做法。
所以在求解最优化问题中,我们还有一个收敛更快的方法:牛顿法,一个以牛顿命名的方法。在学习牛顿法之前,我们必须要知道,牛顿法也是一个迭代算法,只不过要比梯度下降法迭代更快由于牛顿法的主要应用是求解方程的跟和进行最优化,这里主要介绍牛顿法求解最优化问题。
二、牛顿法优化原理
首先,我们知道对于一个一元函数 g ( x ) g(x) g(x),我们可以对其进行泰勒展开,例如,对 g ( x ) g(x) g(x)进行二阶泰勒展开,结果为:
g ( x ) ≈ g ( x k ) + g ′ ( x k ) ( x − x k ) + 1 2 g ′ ′ ( x k ) ( x − x k ) 2 g(x) \approx g({x_k}) + {g'}({x_k})(x - {x_k}) + \frac{1}{2}{g''}({x_k}){(x - {x_k})^2} g(x)≈g(xk)+g′(xk)(x−xk)+21g′′(xk)(x−xk)2
如果我们的目的是求解 g ( x ) g(x) g(x)的最小值,那么一般的做法都是找到 g ( x ) g(x) g(x)导数等于零的点,所以需要对 g ( x ) g(x) g(x)进行求导并令其等于0:
g ′ ( x k ) + g ′ ′ ( x k ) ( x − x k ) = 0 g'({x_k}) + g''({x_k})(x - {x_k}) = 0 g′(xk)+g′′(xk)(x−xk)=0
⇒ x = x k − 1 g ′ ′ ( x k ) g ′ ( x k ) \Rightarrow x = {x_k} - \frac{1}{{g''({x_k})}}g'({x_k}) ⇒x=xk−g′′(xk)1g′(xk)
即可以推导出牛顿法的迭代式了,把 x x x替换成 x k + 1 x_{k+1} xk+1,则我们就可以将牛顿法的公式理解为搜索方向为 − 1 g ′ ′ ( x k ) g ′ ( x k ) -\frac{1}{{g''({x_k})}}g'({x_k}) −g′′(xk)1g′(xk),步长为1的迭代方法。
还记得在梯度下降法中搜索方向为 − g ′ ( x k ) -g'(x_{k}) −g′(xk),步长为 λ \lambda λ学习率。牛顿法中没有学习率这个概念,即默认牛顿法的学习率为1。在了解了牛顿法的相关数学原理之后,我们可以对其进行实验。
三、算法实现
如果使用牛顿法来解决最优化问题,我们需要提前认识一个新概念:黑塞矩阵(Hesse),下面是二元函数的黑塞矩阵的定义:
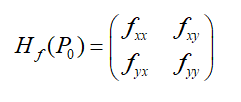
如果推广当 n n n维函数就是改变为 n × n n×n n×n的矩阵即可。将黑塞矩阵记为 H k H_{k} Hk,之所以说牛顿法的计算量很大就是因为每一次迭代过程中都需要计算Hesse矩阵的逆矩阵: H k − 1 H^{-1}_{k} Hk−1
下面是牛顿法迭代是步骤:

选取函数为 f = 100 ( 2 x 1 2 + 2 ) 2 + x 2 2 f = 100(2x^{2}_{1}+2)^{2}+x^{2}_{2} f=100(2x12+2)2+x22,下面使用牛顿来找到函数的最小值,实现语言为MATLAB。
% 牛顿法求解二元极值问题
% f=100*(2*x1^2+2)^2+x2^2;
syms x1 x2;
f=100*(2*x1^2+2)^2+x2^2;
% 构造目标函数的f一阶导
fx = diff(f,x1);
fy = diff(f,x2);
gf = [fx,fy]';
% 求Hesse矩阵
fxx = diff(fx,x1);
fxy = diff(fx,x2);
fyx = diff(fy,x1);
fyy = diff(fy,x2);
H = [fxx,fxy;fyx,fyy];
% 初始化
ess = 1e-5; % 精度
x0 = [5,1]; % 初始点
xk = x0'; %
fk = subs(f,[x1,x2],x0); % 计算初始值
gk = subs(gf,[x1,x2],x0); % 计算初始导数
Hk = subs(H,[x1,x2],x0); % 计算初始黑塞矩阵
k = 0;
% 进入循环
while((norm(gk)>ess)&&(k<10))
% 迭代进行
dk = -Hk\gk;
xk = xk+dk;
% 计算新的函数值和梯度
fk = subs(f,[x1,x2],xk');
gk = subs(gf,[x1,x2],xk');
Hk = subs(H,[x1,x2],xk');
% 记录迭代次数
k = k + 1;
end
xk=vpa(xk,10);
fk=vpa(fk,5);
disp(['最小值根为:',num2str(double(fk))])
disp(['迭代次数为:',num2str(k)])
结果为

从代码量上看,用牛顿法求解二元最优化问题的代码确实要比梯度下降法要多,这其中最大的差别就是,牛顿法每次迭代都需要计算黑塞矩阵,其是二次收敛,收敛速度必定会比梯度下降法快很多。
在代码中有一步需要说明一下,就是-Hk\gk这个,其实是matlab中的一种特殊写法,其表达的意思就是对Hk取逆然后与gk相乘。
总结
牛顿法和梯度下降法都可以用来求解最优化问题,它们各自有各自的特点。
牛顿法的特点:
- 二阶收敛,收敛的速度非常快
- 计算黑塞矩阵的逆矩阵比较麻烦,而且有的时候运行速度还没有梯度下降法快。
- 不能保证牛顿法的迭代方向一定是沿着函数值的下降的方向
牛顿法虽然比梯度下降法的收敛速度要快很多,但是在面临维数较大时,牛顿法的计算黑塞矩阵的步骤又比较繁琐,而且最致命的是牛顿法的迭代方向不一定就是沿着函数值的下降方向。那么为了解决这两点,分别可以采用拟牛顿法和阻尼牛顿法这两种改进算法进行完善。
特别要注意的是,当初始点远离极小值点时,牛顿法可能还会不收敛,原因之一就是牛顿方向 d = − ∇ 2 f ( x ) − 1 ∇ f ( x ) d=-\nabla^{2}f(x)^{-1}\nabla f(x) d=−∇2f(x)−1∇f(x)不一定是下降方向,如果经迭代,目标函数值可能上升。此外即使函数值下降,得到的点也不一定就是沿着牛顿方向的最好点或者是极小点。
牛顿法迭代方向不一定就是目标函数值下降方向证明:
机器学习笔记-牛顿法搜索方向的相关证明