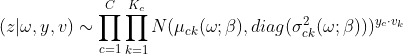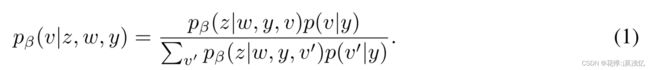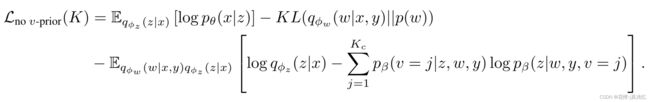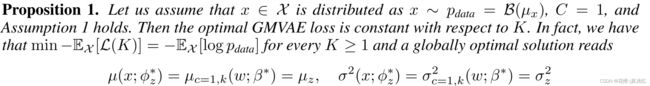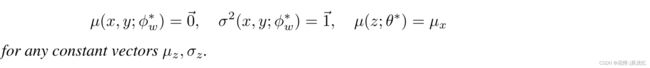【开集识别论文解读】GMVAE——AAAI2021
论文原文：Open-Set Recognition with Gaussian Mixture Variational Autoencoders
目录
Abstract
1. Introduction
2. Related Work
3. Gaussian mixture variational autoencoders
3.1 Gaussian mixture variational autoencoders with multiple subclusters per class
3.2 Modification of the ELBO: removing v-prior
3.3 Open-set classification algorithms
4. Identifying the number of subclusters in each class
5. Experimental result
Abstract
开集识别的目标是将测试样本分为训练中见过的已知类，或将其作为未知类拒绝。现有的深度开集识别分类器通常训练显式的闭集分类器，不联合使用重构的方法削弱了潜在表示区分未知类的能力。在本文中，训练模型在潜在空间中配合学习重建和执行基于类的聚类。本文提出的高斯混合变分自动编码器（GMVAE）通过大量实验，获得了更准确和鲁棒的开集分类结果，F1平均提高29.5%。
1. Introduction
大部分分类算法都是为闭集分类的场景设计的，这意味着所有的测试类别都会在训练过程中见到。然而，现实世界的应用需要在开放场景下进行，在测试过程中会出现训练过程中未见过的未知类。例如，自动驾驶汽车中的计算机视觉系统必须对许多不同的物体进行分类和导航，这些类别数量是无限的，在训练中不可能看到所有类。开集识别解决的就是分类任务的这种泛化问题。
开放集下的学习有几个方面，在本文中重点关注C已知类的（C+1）类分类训练。这个（C+1）类包括所有不属于任何已知类的未知测试样本。训练数据中没有第C+1类中的未知类。为此，本文提出了一种新型的有监督高斯混合变分自动编码器（GMVAE）。瓶颈潜在层同时学习重构并执行基于类的聚类。这允许潜在表示捕获互补结构和分类器信息。此外，潜在层具有在每个类中形成多个子集群的显式能力。这挑战了许多分类方法的隐式假设，即类的嵌入是一个凸集，因此最好用一个质心来表示。这为捕获互补结构和分类器信息提供了进一步的灵活性。
本文贡献如下：
- 在第三章中，推导了GMVAE来学习嵌入并修正其目标函数，以使开集识别更易于实现。
- 提出了一种新的简单的开集分类算法，该算法利用学习嵌入的“不确定性”阈值。
- 在第四章之后，给出了关于子聚类数量的分析结果，以及由此产生的启发式程序，用于确定每个类别中适当数量的子聚类。
- 在第五章中，在三个标准数据集上进行了开集分类实验。我们的实验结果有两个方面。首先，GMVAE在准确性和对越来越多的未知类的鲁棒性方面都优于最先进的深度开集分类器。其次，使用极值理论（EVT）来推断类归属可能不太合适，因为我们发现我们的算法和另一个简单的算法始终优于它。（个人不是很同意这种说法）
2. Related Work
在本文中，使用的baseline是CROSR，因为它达到了SOTA的性能并且依赖于类似的双重重建分类学习框架。
3. Gaussian mixture variational autoencoders
在本节中，介绍了完整的开集识别过程，它遵循与先前工作相同的两个阶段：首先，学习（子）聚类已知类的潜在表示，然后，在该嵌入上应用开集分类算法。本文提出的GMVAE模型是高斯混合变分自动编码器的扩展。
变分自动编码器（VAE）假设数据是由单峰高斯先验生成的。在【10】中，作者选择高斯混合作为直观的扩展。为了通过重新参数化技巧保持标准反向传播，改变了标准VAE体系结构。生成模型分解为
，通过以下过程从潜变量
，
和
生成样本
:
,
其中K是用户定义的混合数量，
、
、
和
分别是由
和
参数化的神经网络。然后将识别模型分解为
，其中
和
参数化了输出高斯后验变分分布均值和对角协方差的神经网络。利用贝叶斯规则，可以根据生成模型的因子写出v-后验项
。为了进行训练，对数证据下限（ELBO）![E_{q(z,w,v | x)}[p_{\beta,\theta}(x,z,w,v)/q(z,w,v | x)]](http://img.e-com-net.com/image/info8/c20d1eb84c124acf9083b9c856ab2fd0.gif){kind=small}
最大化。在3.1和3.2中介绍了GMVAE的推导和差异，最后介绍了新的开集分类算法，该算法利用3.3中的“不确定性”阈值。
ELBO，即 Evidence Lower Bound，证据下界。这里的证据指数据或可观测变量的概率密度。假设
表示一系列可观测数据集，
为一系列隐变量(latent variables)。则可用
表示联合概率，
为条件概率，
为证据。那么，贝叶斯推理需要求解的就是条件概率，即：
然而，对很多模型而言，计算
因此，无法直接计算
来近似
，要得到最佳的
其中，KL散度可以表示为：
由于KL散度大于0，进而我们可以求得:
因此，有：
![KL(q(z)||p(z|x))=E[log q(z)]-E[log p(z,x)]+E[log p(x)]](http://img.e-com-net.com/image/info8/6975f8f9d37a43ca80e65afe70d144ba.gif){kind=small}
![logp(x)\geq E[logp(z,x)]-E[logq(z)]](http://img.e-com-net.com/image/info8/bcd31e8e30e449a1b7525b52efe3f3c8.gif){kind=small}
![ELBO(q)=E[logp(z,x)]-E[logq(z)]](http://img.e-com-net.com/image/info8/71e8b94617fa4b849e49b8cd982f5878.gif){kind=small}
3.1 Gaussian mixture variational autoencoders with multiple subclusters per class
GMVAE模型将[10]中的无监督学习框架非平凡地扩展到每个类的基本高斯混合先验。对于表示方法，有C个已知类，每个类由
个子簇组成，其中
、 样本
和标签
作为一个热向量，包含标记的已知数据集
。GMVAE的生成过程
以类为条件：
通常认为
对于每个类都是一致的。识别模型分解为
，其中
。我们使用网络
对变分因子进行参数化，网络输出变分分布的均值和对角协方差，并将其形式指定为高斯后验概率：
分解中有一个
因子，因为
因子可以用生成因子来表示，从而减少了可训练参数的数量。使用Bayes，我们可以将
重写为
另一个好处是，只需一次前向传播，就可以计算所有v的。然后， GMVAE的ELBO由下式给出：
由于
是用户定义的，因此ELBO对K的依赖性是明确的，并在后面的分析中使用。重构项促进了对重构样本有意义的潜在表示。潜在覆盖项试图基于类对潜在表示进行子聚类。w-先验项和子聚类v-先验项使这些后验项更接近其各自的先验项。
3.2 Modification of the ELBO: removing v-prior
在本小节中，本文建议从原始ELBO中删除v-先验项，以使GMVAE更利于开放集识别，原因有两点：首先，最小化v-先验项![E_{q_{\phi_\omega}(w | x,y)q_{\phi_z}(z | x)}[KL(p_\beta(v | z,w,y)|| p(v | y))]](http://img.e-com-net.com/image/info8/adc501e83a3d4ca6ae4597013b82aacf.gif){kind=small}
与类内不同子聚类的目标直接冲突。我们的目标是在类的潜在表示中创建不相交的子聚类，以便进一步提供更大的重构灵活性，并减轻类的嵌入是凸集的假设。然而，请注意，当每个、
和
的
时，v-先验项最小化。结合（1）和统一的
，这反过来意味着每个、、
和
的
。由于潜在覆盖项的最大化，等效生成模型分布导致潜在子集群中的模式崩塌。
第二，如4中的命题2所证明的，在没有v-先验项的情况下，C=1的最佳GMVAE损失相对于K是不增加的。这是一个分析结果，它提供了一个启发式程序，用于确定每个类别使用的适当数量的子聚类。鉴于这两个原因，对于5中的所有实验，我们使用了以下改进的ELBO：
从某种意义上说，这就好像我们没有对子集群分布施加先验知识一样。虽然我们也可以否定v-先验项，但简单地去掉它实际上会得到最好的实验结果。
3.3 Open-set classification algorithms
开集识别的最新文献中，通过将Weibull分布拟合到类的潜在表示与其质心之间的内部距离来建模类归属性几乎已成为普遍现象。事实上，baseline方法CROSR通过该EVT框架实现了SOTA的性能。然而，我们的实验表明，两个简单得多的算法可以显著优于CROSR的基于EVT的分类算法。虽然将分布拟合到内联距离可能是在类的质心周围确定超球体密度的有效方法，但我们认为它对这些内部因素过于敏感。如果一个类的样本的潜在表示是“错误分类”的，并且远离其质心，那么得到的分布拟合将极为偏斜，并导致不准确的预测。这种可能的负面影响对于未优化每个类中较低内部分布的嵌入来说被严重放大。例如，CROSR的嵌入由闭集、softmax分类器的激活向量组成；这鼓励向量的元素趋向于正无穷大和负无穷大。
接下来，将介绍本文实现的两个简单的开集分类算法。当GMVAE在潜在空间中输出高斯分布时，我们只需选择平均值
作为有效的潜在表示。算法1是从[3]中所谓的离群值得分推导出来的，但最恰当地描述为最近质心距离的最近质心阈值。该算法被修改为每个类包含多个子集群。
实验结果表明，距离最近的质心距离阈值更适合于围绕各自质心的超球体。然而，CROSR的EVT方法有一个类似的缺点，即距离是旋转对称度量。它不包括任何方向感。我们有理由认为，在任何基于最近质心的算法中，从开集分类的角度来看，质心之间的开放空间构成了最大的风险。这导致了第二种算法，该算法在“不确定性”量U上使用了一个新的阈值。我们将U定义为到最近质心的距离与到所有其他质心的平均距离之间的比率。因此，如果U=1，测试样本的潜在表示与所有质心等距，这可以解释为不可分类。如果U=0，测试样本的潜在表示就是一个质心，这意味着分类中没有歧义。这样，算法2包含了质心之间方向的概念，因为U会更严重地惩罚质心之间的开放空间。
4. Identifying the number of subclusters in each class
由于每个类中的子集群数量是用户定义的，因此确定适当的数量对于模型的使用至关重要。自然而然地想到，针对越来越多的子集群，对每个类的数据单独迭代应用GMVAE。考虑到重建和聚类目标，经验模型损失自然会告诉我们最佳的子聚类数。这类似于在k均值聚类中增加k，并研究由此产生的惯性图。为此，在本节中，我们首先给出了关于
对最佳
（单级）GMVAE损失影响的分析结果。这将导致我们的启发式程序，用于确定每个类中理想的子集群数量。
通过两个无限制的神经网络假设，我们能够证明关于K对最优GMVAE损失的影响的两个命题。第一个命题表明，当一个类中确实只有一个子类，并且我们知道它的分布时，最优损失相对于K是常数。
第二个命题没有数据假设，但表明最优损失相对于K是准非递增的。然而，它确实证明了序列差分的一致下界。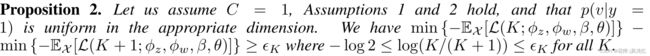 
5. Experimental results
实验结果证明了一些发现：首先，基于EVT的开集分类可能不合适，因为简单的最近质心程序始终优于它。其次，即使没有子聚类的额外好处，与CROSR相比，
的GMVAE通常会导致更适合于开放集识别的潜在表示。最后，类内的子聚类代表了一种支持双重监督重建嵌入的方法。
每个数据集都有以下组成：训练数据只包含来自C类的标记样本。验证集包含来自相同C类的样本和来自附加Q类的样本，这些样本都被视为C+1类。验证集用于确定阈值。最后，测试集与验证集具有相同的分布。
应用了四种模型和分类算法组合：（i）CROSR与CROSR的EVT（CROSR+EVT），（ii）CROSR与算法1（CROSR+NC-D），（iii）GMVAE与算法1（GMVAE+NC-D），以及（iv）GMVAE与算法2（GMVAE+NC-U）。CROSR+NC-D和GMVAE+NC-D旨在直接比较潜在表示对开集识别的适应性。