RSA大数运算实现（1024位）（2）

接上一篇文章

  在有了大数运算库之后，实现RSA完全不在话下了！

RSA算法

①随机选择两个大素数p和q，计算n=p·q，以及φ(n)=(p-1)·(q-1) ；
②选择e=65537，如果不满足(e,φ(n))=1，则选择一个随机整数(e,φ(n))=1。
③求出私钥d，使得e·d=1(mod φ(n))。
④加密时，明文为M，密文C=M^e mod n；
⑤解密时，密文为C，解密后明文M’= C^d mod n

产生大随机数

产生指定位数的大随机数，如p的bits=524位，q的bits=500位，这样后面可以满足n大致为1024位（可能为1023位）。
①产生位数为bits的大数bignum的函数为int genBN(BN result, int bits)，利用sha-1结果产生bits个二进制位的大数result;
②产生方法为，对于从低到高每一位（一位包含了32个二进制位），调用void writerand(char * addr)函数，往addr中写一个随机数，然后调用之前写的SHA-1函数，计算addr出随机数文件的哈希值，然后取32个二进制位(8个十六进制位，也就是8个哈希结果的字符)。
③最高位(最高的可能有1-32个二进制位)需要特殊处理，因为最高如果是要32位，产生的哈希值第一位如果是A以下，如0-9，那最高就没有32位，得到的大数会小于bits。这种情况下，特殊化处理，多次产生直到产生的是所要的为止。其它时候可以左右移位来满足最高位的需求。

产生指定位数素数

  由int findprime(BN a, int bits)函数实现，该函数调用了genBN(BN result, int bits)函数产生随机数，调用了int fermat_b(BN a)费马检测函数对大数进行素性检测，同时它利用了exclu()函数预先产生的前几十个素数的乘积结果，利用了gcd_b(BN a, BN b, BN & result)函数求公因子。同时需要用到SETONEBIT_B(BN num, uint32_t u)函数设置大数num为一个uint32_t的数u。用到了加法函数add_b(BN a, BN b, BN sum)，过程如下：

(1)首先读取前20个素数的乘积fac，第20个素数存在temp3中；
(2)随机产生满足位数要求的大数bignum；
(3)求公因子gcd_b(fac,bignum,gcd)，如果gcd=1，就拿这个大数去做费马检测步骤(7)。如果gcd比第20个素数还要大，或者很不幸这个大数是偶数gcd=2或者gcd比temp3大，就回到(2)；
(4)对大数进行微调，初始化微调变量linshi=2，循环变量i=0；
(5)大数bignum加上linshi，得到调整后的adjnum，对adjnum和fac求最大公因子gcd。
(6)如果gcd为1，就进行费马检测，步骤(7)，linshi设为2。如果gcd不是1，且gcd (7)如果费马检测结果为1，则判定产生的是素数，否则回到(2)。

公钥e的选取

默认选择e=65537,但是计算(e,φ(n))可能不为1，这种情况下，就随机选择一个17位的e，使用findprime()，选择好以后存在e的路径中。

私钥d的产生

①inv_b(BN a, BN n, BN & x)函数实现，该函数调用了gcd_b(BN a, BN b, BN & result)函数，先求公因子判断是否存在逆元，然后才求逆。
②求逆时，对于inv_b(a,n,x)，初始化u=1,g=a,v1=0,v3=n.
③用div_l(g,v3,q,t3)计算带余除法,g=q·v3+t3，令t1=u-q·v1 (mod n )，u=v1，g=v3，v1=t1，v3=t3。
④如果v3=0，则把u赋值给x，作为结果，否则回到步骤②。

加密

加密过程为模幂运算 C=M^e mod n
①使用模平方算法，配合调用modmul()模乘函数；
②对指数e进行二进制展开，初始化a=1，b=M，m=n。
③对于e的二进制展开，从低到高一位位来判断，b=b*b (mod m)，如果这一位为1，则a=a*b(mod n)，否则a=a；
④最后e的二进制位都算完了，a就是结果。

解密

解密时因为已知p和q，可以使用中国剩余定理加速解密，加速以后的时间是加速以前的一半：
①中国剩余定理在void crt_b(BN a, BN b, BN p, BN q, BN & result)中实现。
②先计算b11和b22，然后得到其中b11 = b mod p, b22 = b mod q：a^b =a^b11= b1 mod p a^b =a^b22 = b2 mod q
③得到方程组 x=b1 mod p
x=b2 mod q
④求逆然后得到结果：
m1=p; m2=q m=m1*m2
M1=m2=q M2=m1=p
M1*M1’=1 mod p M2*M2’=1 mod q
result= b1*M1’*M1 + b2* M2’*M2 mod(m)

测试

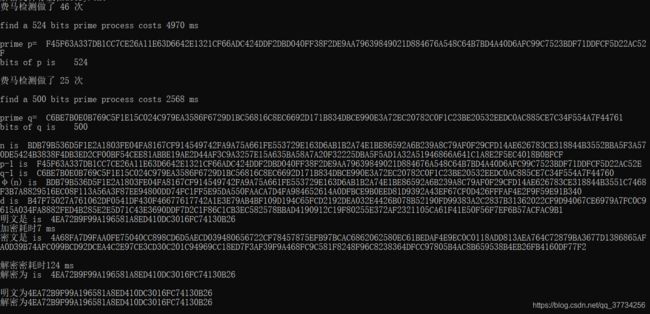
1.加密解密过程，用之前产生好的p和q，设置的e=65537，加密时间明显比解密时间短，其中明文是某个文件的哈希值。

2.当默认的e=65537与φ(n)不互素时，会随机产一个17位的素数，这里产生的为1B011。

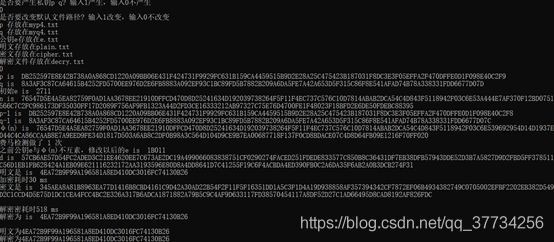
3.完整的从产生密钥、加密、解密的过程如下，时间比较长，尤其产生密钥，一般500位的要平均10秒左右，使用VS打开优化以后则一般2-5秒，快的时候1秒。

4.采用优化编译时，速度比较快

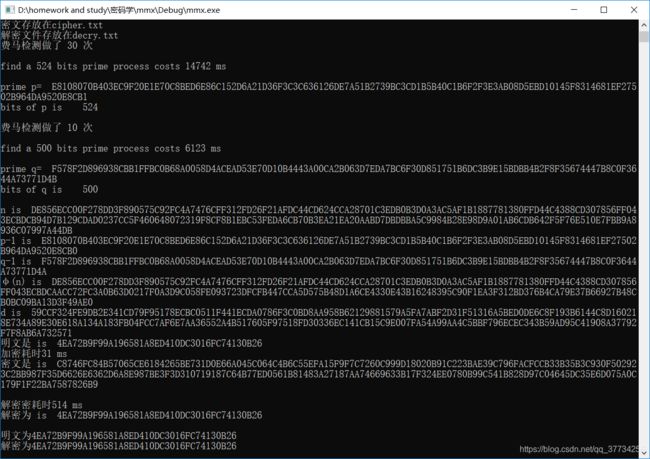
5.因为比较难比较到底加解密是否正确，可以调用SHA-1函数来验证，这时SHA-1每次调用必须对初始化向量赋予初值，和之前的mysha1()用来随机寻找素数时的每调用一次都有一个状态时完全不一样，之前那个状态要是每次都是定值，寻找素数很慢，而这里要验证，所以必须初值每次都固定。

代码如下

int main()
{
	BN p, q, n, eula, e, d;
	BN p_1, q_1;
	BN plain;//明文
	BN cry;//加密以后
	BN dec;//解密以后

	BN temp1 = { 0 }, temp2 = { 0 }, temp3 = { 0 };//用来测试

	memset(p, 0, BNSIZE);
	memset(q, 0, BNSIZE);
	memset(p_1, 0, BNSIZE);
	memset(q_1, 0, BNSIZE);
	memset(n, 0, BNSIZE);
	memset(eula, 0, BNSIZE);
	memset(e, 0, BNSIZE);
	memset(d, 0, BNSIZE);
	memset(plain, 0, BNSIZE);
	memset(cry, 0, BNSIZE);
	memset(dec, 0, BNSIZE);
	
	//产生p和q，一般情况下是有了的不用自己产生
	char p_path[81] = "myp4.txt";
	char q_path[81] = "myq4.txt";
	char e_path[81] = "e.txt";
	char plain_path[81] = "plain.txt";
	char cipher_path[81] = "cipher.txt";
	char decry_path[81] = "decry.txt";


	int ifgen = 0;//是否产生私钥
	int ifset = 0;
	cout << "是否要产生私钥p q? 输入1产生，输入0不产生\n";
	cin >> ifgen;
	cout << "是否要改变默认文件路径? 输入1改变，输入0不改变\n";
	cout << "p 存放在" << p_path << endl;
	cout << "q 存放在" << q_path << endl;
	cout << "公钥e存放在" << e_path << endl;
	cout << "明文存放在" << plain_path << endl;
	cout << "密文存放在" <<cipher_path << endl;
	cout << "解密文件存放在" << decry_path << endl;
	cin >> ifset;

	if (ifset == 1)
	{
		memset(p_path, 0, sizeof(p_path));
		memset(q_path, 0, sizeof(q_path));
		memset(e_path, 0, sizeof(e_path));
		memset(plain_path, 0, sizeof(plain_path));
		memset(cipher_path, 0, sizeof(cipher_path));
		memset(decry_path, 0, sizeof(decry_path));
		cout << "请输入p存放路径"<<endl;
		cin >> p_path;
		cout << "请输入q存放路径" << endl;
		cin >> q_path;
		cout << "请输入e存放路径" << endl;
		cin >> e_path;
		cout << "请输入明文存放路径" << endl;
		cin >> plain_path;
		cout << "请输入密文存放路径" << endl;
		cin >> cipher_path;
		cout << "请输入解密后存放路径" << endl;
		cin >> decry_path;


		cout << "设置以后: " << endl<<endl;

		cout << "p 存放在" << p_path << endl;
		cout << "q 存放在" << q_path << endl;
		cout << "e 存放在" << e_path << endl;
		cout << "明文存放在" << plain_path << endl;
		cout << "密文存放在" << cipher_path << endl;
		cout << "解密文件存放在" << decry_path << endl;

	}

	if (ifgen == 1)//为1则产生
	{
        genpq(p_path, q_path);
		SETONEBIT_B(e, 10001U);
		writebn(e_path, e);
		readbn(p, p_path);
		readbn(q, q_path);
		readbn(e, e_path);
	}
	else
	{	
		readbn(p, p_path);
		readbn(q, q_path);
		readbn(e, e_path);
		cout << "p is  " << bn2str(p) << endl;
		cout << "q is  " << bn2str(q) << endl;
		cout << "初始e is  " << bn2str(e) << endl;
	}


	//获取p/q
	

	//计算n
	mul(p, q, n);
	cout << "n is  " << bn2str(n) << endl;
	writebn("n.txt", eula);

	subuint_b(p, 1U, p_1);
	cout << "p-1 is  " << bn2str(p_1) << endl;

	subuint_b(q, 1U, q_1);
	cout << "q-1 is  " << bn2str(q_1) << endl;

	mul(p_1, q_1, eula);
	cout << "φ(n) is  " << bn2str(eula) << endl;
	writebn("fn.txt", eula);
	
	//一般公钥e =65537
	//SETONEBIT_B(e, 10001U);

	gcd_b(e, eula, temp3);
	if (cmp_b(temp3, ONE_BN) != 0) {
		while (cmp_b(temp3, ONE_BN) != 0)//如果不互素！！！悲剧了
		{
			findprime(e, 17);
			gcd_b(e, eula, temp3);
		}
		cout << "之前公钥e与φ(n)不互素，修改以后的e is  " << bn2str(e) << endl;
		writebn("e.txt", e);
	}
	


	//私钥d  ed =1 mod φ(n)
	inv_b(e,eula, d);
	cout << "d is  " << bn2str(d) << endl;
	writebn("d.txt", d);
	//获取明文
	readbn(plain, plain_path);
	cout << "明文是 is  " << bn2str(plain) << endl;
	//加密
	int time1 = clock();
	modexp_b(plain, e,n, cry);
	printf("加密耗时%d ms\n", clock() - time1);
	cout << "密文是 is  " << bn2str(cry) << endl;
	
	writebn(cipher_path, cry);

	//解密
	int time2 = clock();
	//modexp_b(cry, d, n, dec);
	crt_b(cry, d, p, q, dec);
	printf("\n解密密耗时%d ms\n", clock() - time2);
	cout << "解密为 is  " << bn2str(dec) << endl;
	writebn(decry_path, dec);



	readbn(temp1, plain_path);
	readbn(temp2, decry_path);

	cout << endl << "明文为" << bn2str(temp1);
	cout  << endl<<"解密为" << bn2str(temp2)<<endl;

	if (checkresult(plain_path, decry_path) == 1)
		cout << "\n加解密正确！" << endl;
	else
		cout << "\n加解密出现错误！" << endl;
	system("pause");
	return 0;
}