机器学习-31-Transformer详解以及我的三个疑惑和解答

Transformer

Transformer的知名应用——BERT——无监督的训练的Transformer。

Transformer是BERT的核心模块

Transformer是一个seq2seq模型，并且大量用到了"Self-attention"，接下来就要讲解一下"Self-attention"用到了什么东西

Sequence

Sequence就会想到RNN，单方向或者双向的RNN。

RNN输入是一串sequence，输出是另外一串sequence。

RNN常被用于输出是一个序列的情况，但是有一个问题——不容易被平行化（并行）。

单向RNN的时候，想要算出b4，必须先把a1，a2，a3都看过才可以算出a4。双向则得全部看完才会有输出。

用CNN取代RNN

于是有人提出用CNN取代RNN

一个三角形是一个filter，输入为sequence中的一段，此刻是将三个vector作为一个输入，输出一个数值。

• 将三个vector的内容与filter内部的参数做内积，得到一个数值，将filter扫过sequence，产生一排不同的数值。
• 会有多个filter，产生另外一排不同的数值

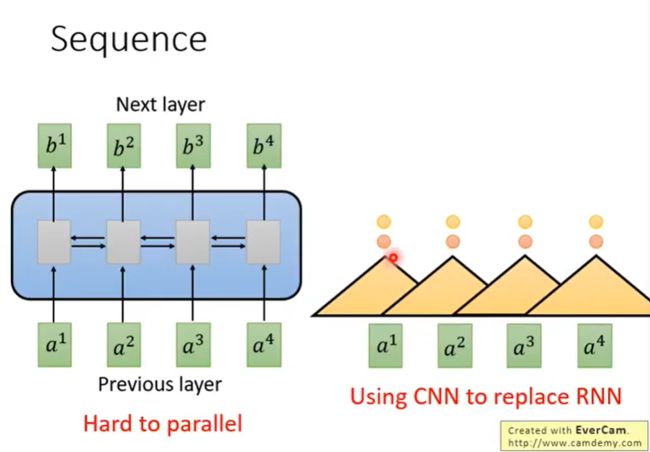
我们可以看到，用CNN也可以做到和RNN类似的效果：输入一个sequence，输出一个sequence。

表面上CNN和RNN都可以有同样的输入输出。

但是每个CNN只能考虑很有限的内容（三个vector），而RNN是考虑了整个句子再决定输出。

CNN也可以考虑更长的信息，只要叠加多层CNN，上层的filter就可以考虑更加多的信息。

eg：先叠了第一层CNN后，叠加第二层CNN。第二层的filter会把第一层的output当作输入，相当于看了更多的内容。

CNN的好处在于可以并行化。
CNN的缺点在于必须叠加多层，才可以看到长时间的信息，如果要在第一层filter就要看到长时间的信息，那是无法做到的。

所以，我们引入了 一个新的想法：Self-Attention

Self-Attention

Self-Attention做的事情就是取代RNN原本要做的事情。
关键： 有一种新的layer—— Self-Attention，输入输出与RNN一样，都是sequence。

特别的地方在于，和双向RNN有同样的能力，每一个输出都是看过整个input sequence，只不过b1 b2 b3 b4是可以同时算出来的，可以并行计算！

Self-attention is all you need(重点)

在此，我先讲将oogle的论文贴出来吧： Attention Is All You Need

输入sequence x1~x4，通过乘上一个W matrix来得到embedding a1~a4，丢入Self-attention，每一个输入都分别乘上三个不同的transformation matrix，产生三个不同的vector q，k，v。

• q代表query，用来match其他人
• k代表key，用来被匹配的
• v代表要被抽取出来的信息

拿每个query q去对每个key k做attention，我们这里用到的计算attention的方法是scaled dot-product，关于这一点，我们，下文中还会有介绍。 [scaled dot-product传送门](#scaled dot-product)

attention本质就是输入两个向量，输出一个分数。

除以$\sqrt{d}$的一个原因是：d是q和k的维度，q和k做inner product，所以q和k的维度是一样的为d。除以$\sqrt{d}$的直观解释为q和k做内积/点积的数值会随着维度增大 他的variance越大，所以除以来$\sqrt{d}$平衡。

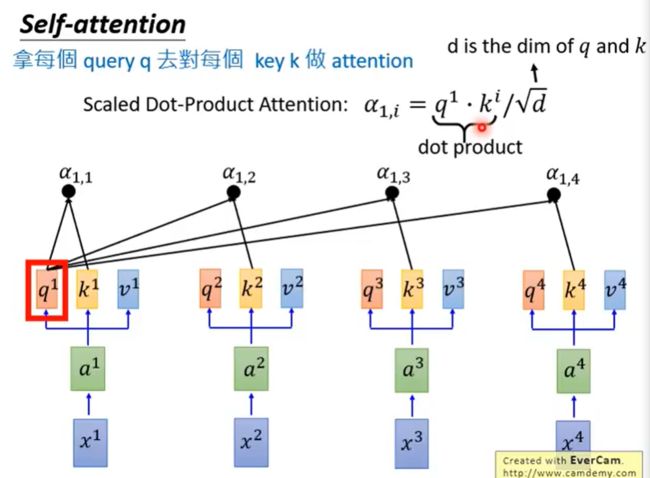
不除以d会梯度爆炸，不收敛，推一推梯度就能的到结果

通过一个softmax函数

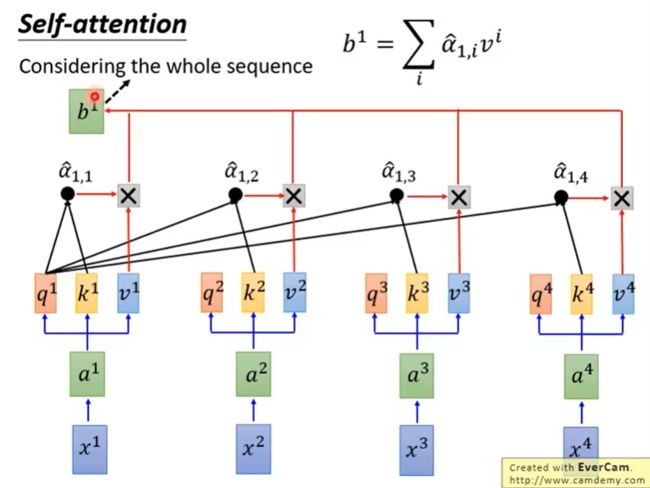
上图，产生b1的时候已经考虑了全部句子的信息

如果现在只想考虑局部的信息，而不是全局的，也是可以做到的，即只需要让右边那些$\alpha$产生出来的值变成0，就只考虑局部了。
如果要考虑全局的信息，就要考虑离他最远的input的vector值的话，只要让那个attention （$\alpha$）有值即可。

相比上面那张图，我还是更喜欢下面这张图：

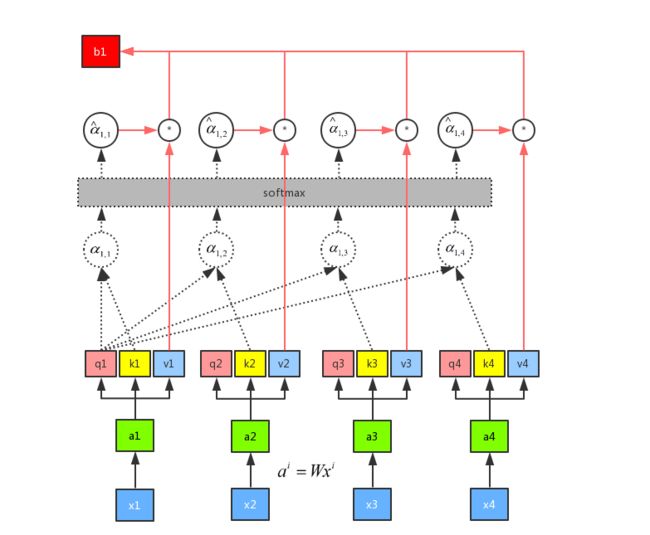
刚刚只是计算了b1，同时也可以计算其他的b

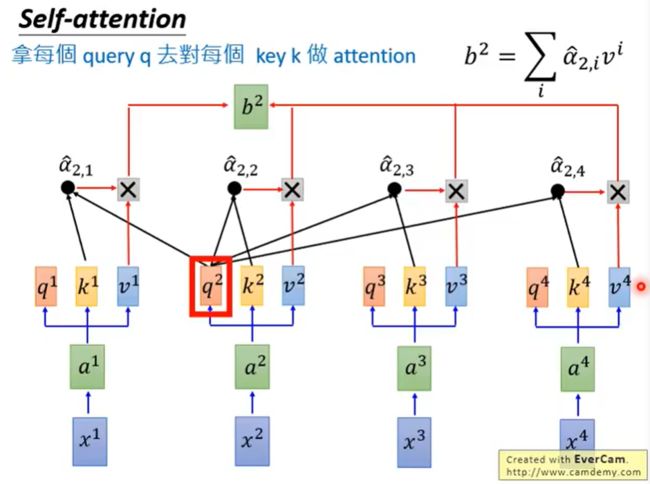
我们来看一下最终完整的流程图:

self-attention做的和RNN的事情是一样的，只不过是平行计算出来的。

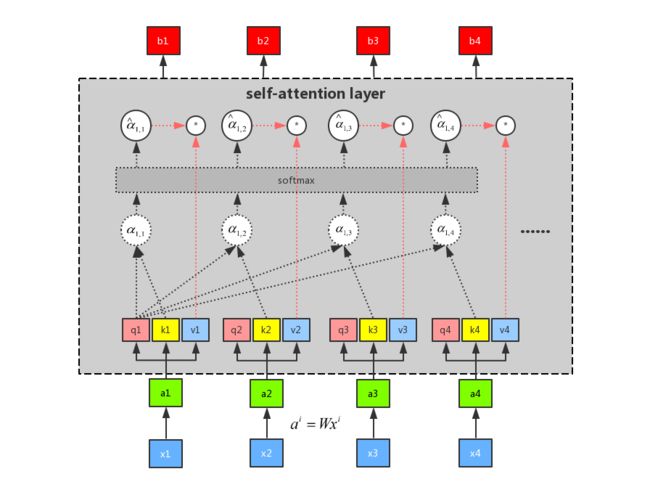
Self-attention是如何并行计算的？ 矩阵运算！

self-attention中所有的运算都可以利用矩阵来进行运算，因此我们就可以使用gpu来进行加速,极大的加快了我们的运算速度。

现在我们就来看看self-attention是如何利用矩阵进行并行计算的吧！！！

看到上面这张图我们应该不陌生，这是我们进行self-attention的第一步。

矩阵运算就是将a1~a4拼起来作为一个matrix I，用 I 再乘以$W^q$，一次得到matrix Q，里面的每一列代表一个q。同理，将matrix I乘以$W^k$和$W^v$可以得到相应的matrix K和marix V。

接下来，拿query q去对每个key k做attention。并对每一列做softmax。

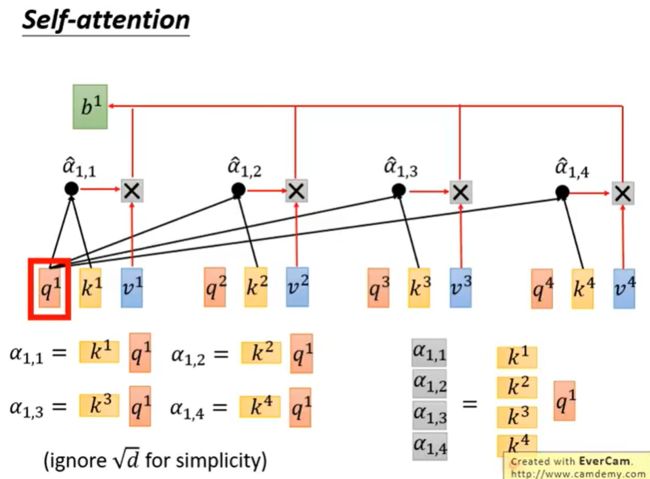
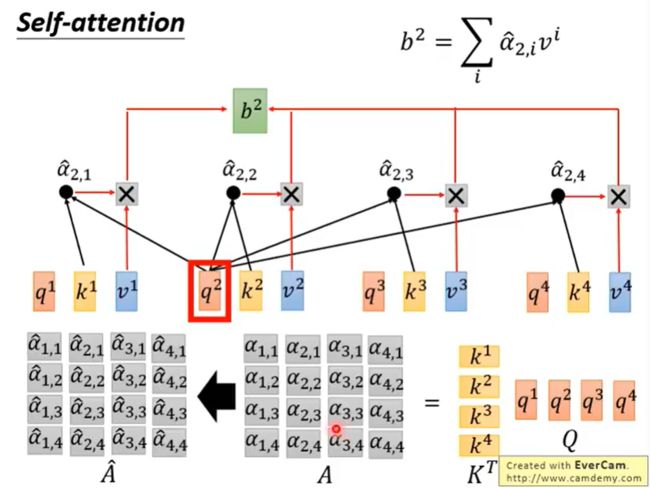
接下来就是根据我们通过softmax得到的结果，考虑每个信息，从而得到我们的一个输出。

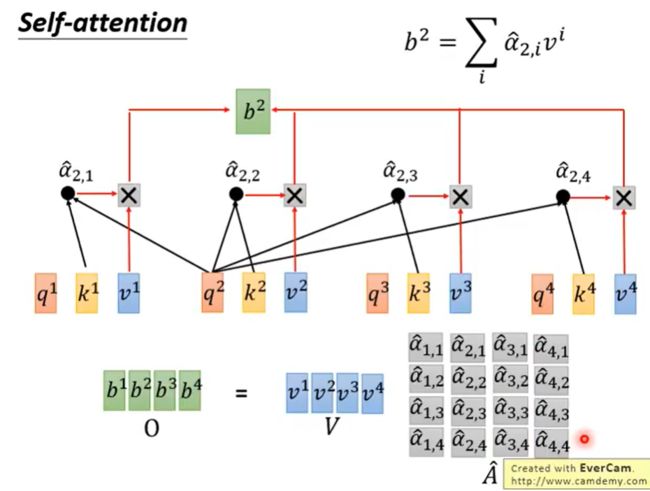
最后，我们将所有矩阵运算整合起来，来回顾一下整个流程。

Multi-head Self-attention(Self-attention的变形 )

通过增加一种叫做“多头”注意力（“multi-headed” attention）的机制，进一步完善了自注意力层，并在两方面提高了注意力层的性能：

1. 它扩展了模型专注于不同位置的能力。在上面的例子中，虽然每个编码都在z1中有或多或少的体现，但是它可能被实际的单词本身所支配。如果我们翻译一个句子，比如“The animal didn’t cross the street because it was too tired”，我们会想知道“it”指的是哪个词，这时模型的“多头”注意机制会起到作用。

2. 它给出了注意力层的多个“表示子空间”（representation subspaces）。接下来我们将看到，对于“多头”注意机制，我们有多个查询/键/值权重矩阵集(Transformer使用八个注意力头，因此我们对于每个编码器/解码器有八个矩阵集合)。这些集合中的每一个都是随机初始化的，在训练之后，每个集合都被用来将输入词嵌入(或来自较低编码器/解码器的向量)投影到不同的表示子空间中。

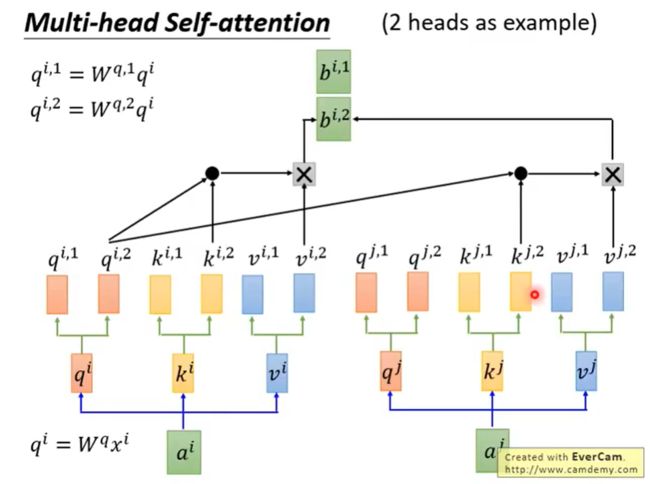
注意一点的是，每个头只能和对应的头进行运算。比如：$q^{i,2}$只能和对应的$k^{i,2}$以及$k^{j,2}$进行运算，而不能和$k^{i,1}$以及$k^{j,1}$进行运算。

算出了$b^{i,1}$和$b^{i,2}$后，给我们带来了一点挑战。前馈层不需要两个矩阵，它只需要一个矩阵！所以我们需要一种方法把这两个矩阵压缩成一个矩阵。那该怎么做？其实可以直接把这些矩阵拼接在一起，然后用一个附加的权重矩阵$W^o$与它们相乘。

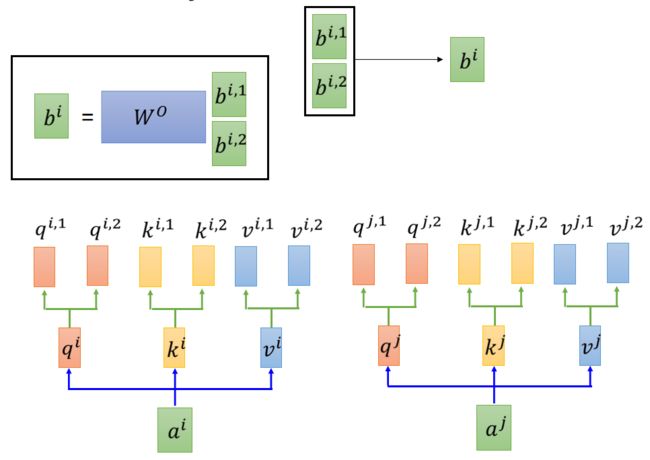
当然我们上面仅仅是二头。其实还可以有好多头，我们再举一个八头的例子：

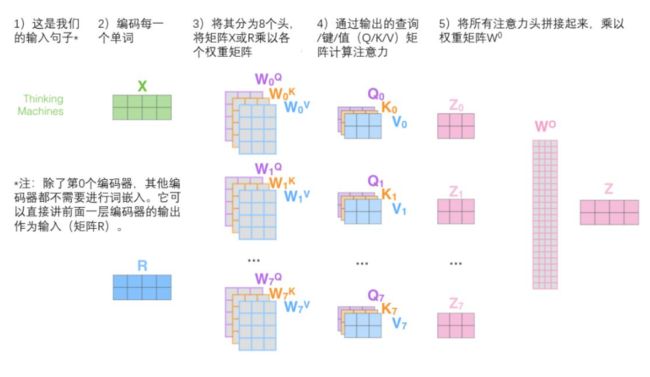
了解了多头机制后，让我们重温之前的例子，看看我们在例句中编码“it”一词时，不同的注意力“头”集中在哪里。

“The animal didn’t cross the street because it was too tired”，我们会想知道“it”指的是哪个词?

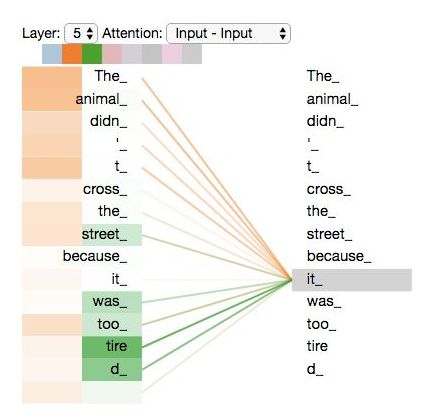
当我们编码“it”一词时，一个注意力头集中在“animal”上，而另一个则集中在“tired”上，从某种意义上说，模型对“it”一词的表达在某种程度上是“animal”和“tired”的代表。

然而，如果我们把所有的attention都加到图示里，事情就更难解释了：

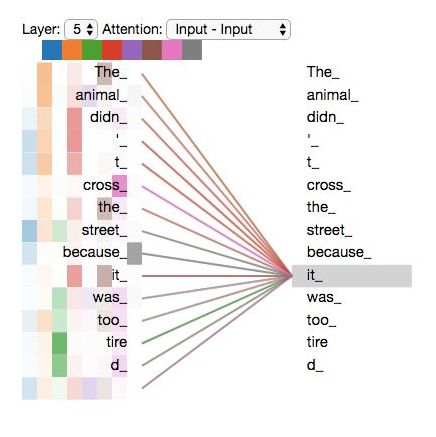
Position Encoding

到目前为止，我们对模型的描述缺少了一种理解输入单词顺序的方法。

为了解决这个问题，Transformer为每个输入的词嵌入添加了一个向量。这些向量遵循模型学习到的特定模式，这有助于确定每个单词的位置，或序列中不同单词之间的距离。这里的直觉是，将位置向量添加到词嵌入中使得它们在接下来的运算中，能够更好地表达的词与词之间的距离。

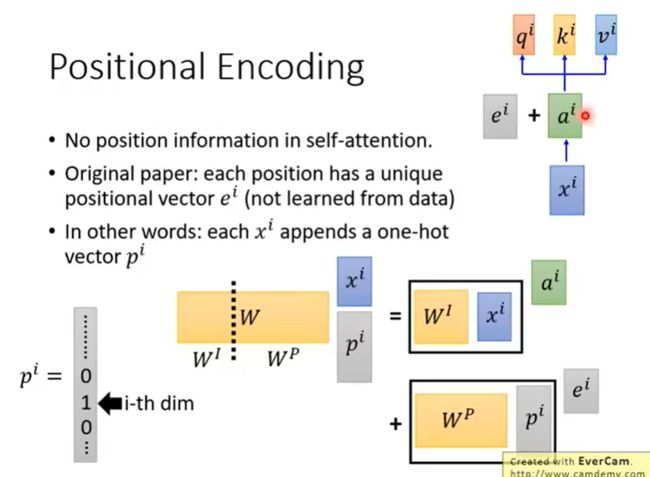
在原始paper中，$e^i$是人手设置的，不是学习出来的。$e^i$代表了位置信息，每个位置$e^i$不同。
paper中将$e^i$加上得到一个$a^i$新的vector，之后和Self-attention操作一样。

Q：那么为什么是$e^i$和$a^i$相加呢？而不是拼接起来呢？
A：把再$x^i$append一个one-hot向量$p^i$，由下图可知，结果是一样的。

为了让模型理解单词的顺序，我们添加了位置编码向量，这些向量的值遵循特定的模式。

如果我们假设词嵌入的维数为4，则实际的位置编码如下：

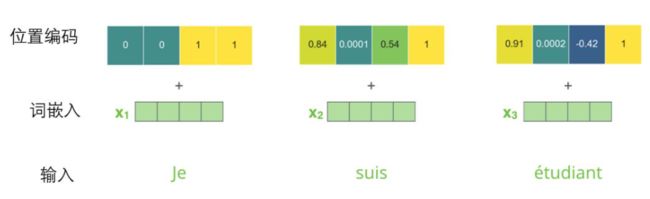
尺寸为4的迷你词嵌入位置编码实例

这个模式会是什么样子？

在下图中，每一行对应一个词向量的位置编码，所以第一行对应着输入序列的第一个词。每行包含512个值，每个值介于1和-1之间。我们已经对它们进行了颜色编码，所以图案是可见的。

20字(行)的位置编码实例，词嵌入大小为512(列)。你可以看到它从中间分裂成两半。这是因为左半部分的值由一个函数(使用正弦)生成，而右半部分由另一个函数(使用余弦)生成。然后将它们拼在一起而得到每一个位置编码向量。

原始论文里描述了位置编码的公式。你可以在 get_timing_signal_1d()中看到生成位置编码的代码。这不是唯一可能的位置编码方法。然而，它的优点是能够扩展到未知的序列长度(例如，当我们训练出的模型需要翻译远比训练集里的句子更长的句子时)。

在实现的时候使用正余弦函数。公式如下：

其中，pos 是指词语在序列中的位置。可以看出，在偶数位置，使用正弦编码，在奇数位置，使用余弦编码。

从编码公式中可以看出，给定词语的 pos，我们可以把它编码成一个 $d_{model}$ (维度)的向量。也就是说，位置编码的每一个维度对应正弦曲线，波长构成了从 $2\pi$ 到 $10000\times 2\pi$ 的等比数列。

上面的位置编码是绝对位置编码。但是词语的相对位置也非常重要。这就是论文为什么要使用三角函数的原因！

pos + k 位置的encoding可以通过pos位置的encoding线性表示。主要数学依据是以下两个公式：

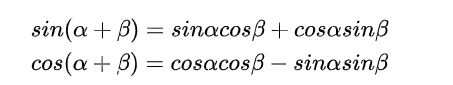
位置为 pos + k 的positional encoding 可以表示如下：

化简如下：

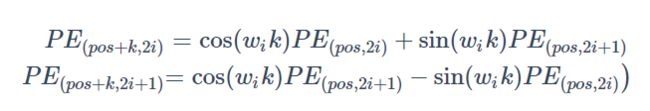
其中与k相关的项都是常数，所以 $P{E}_{pos+k}$可以被 $P{E}_{pos}$线性表示。

由于

所以i越大，周期就越大。周期的范围从 2π到 2π⋅10000

具体实现会在下面给出。 传送门

Seq2Seq with Attention

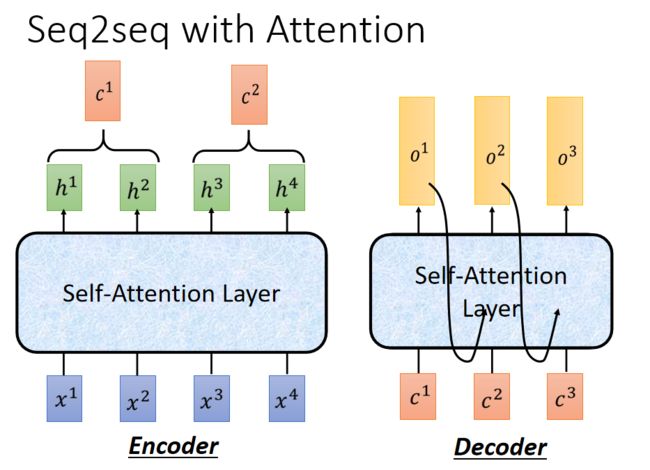
光看上面这张图我们可能并不能直观的看出整个过程，索性谷歌做了一张动图来描述整个过程，让我们一起来看一下吧。

这个图的encoding 过程， 主要是self attention, 有三层。 接下来是decoding过程， 也是有三层， 第一个预测结果 符号， 是完全通过encoding 里的attention vector 做出的决策。 而第二个预测结果Je, 是基于encoding attention vector & attention vector 做出的决策。按照这个逻辑，新翻译的单词不仅仅依赖 encoding attention vector， 也依赖过去翻译好的单词的attention vector。 随着翻译出来的句子越来越多，翻译下一个单词的运算量也就会相应增加。 如果详细分析，复杂度是 （$n^{2d}$）, 其中n是翻译句子的长度，d是word vector 的维度。

Transformer(重点)

简介

Transformer中抛弃了传统的CNN和RNN，整个网络结构完全是由Attention机制组成。更准确地讲，Transformer由且仅由self-Attenion和Feed Forward Neural Network组成。一个基于Transformer的可训练的神经网络可以通过堆叠Transformer的形式进行搭建，作者的实验是通过搭建编码器和解码器各6层，总共12层的Encoder-Decoder，并在机器翻译中取得了BLEU值得新高。

作者采用Attention机制的原因是考虑到RNN（或者LSTM，GRU等）的计算限制为是顺序的，也就是说RNN相关算法只能从左向右依次计算或者从右向左依次计算，这种机制带来了两个问题：

1. 时间片 $t$ 的计算依赖 $t-1$ 时刻的计算结果，这样限制了模型的并行能力；
2. 顺序计算的过程中信息会丢失，尽管LSTM等门机制的结构一定程度上缓解了长期依赖的问题，但是对于特别长期的依赖现象,LSTM依旧无能为力。

Transformer的提出解决了上面两个问题，首先它使用了Attention机制，将序列中的任意两个位置之间的距离是缩小为一个常量；其次它不是类似RNN的顺序结构，因此具有更好的并行性，符合现有的GPU框架。论文中给出Transformer的定义是：Transformer is the first transduction model relying entirely on self-attention to compute representations of its input and output without using sequence aligned RNNs or convolution。

基本架构

接下来的这张图才是重点，上面介绍的仅仅是Transformer完整架构中的某个部分，不过也不要慌，基本上面我们都有提及。

更加具体一点：

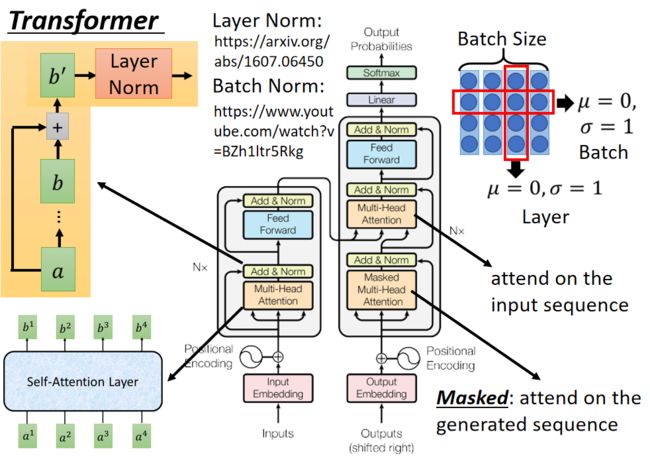
Encoder

在 Encoder 中，Input 经过 embedding 后，要做 positional encodings

Encoder由 6 层相同的层组成，每一层包括2个sub-layers：

• 第一部分是 multi-head self-attention
• 第二部分是 position-wise feed-forward network，是一个全连接层

两个部分，都有一个残差连接(residual connection)，然后接着一个 Layer Normalization。

Decoder

和 encoder 类似，decoder 也是由6个相同的层组成，但每一个层包括以下3个sub-layers:

• 第一个部分是 multi-head self-attention mechanism
• 第二部分是 multi-head context-attention mechanism
• 第三部分是一个 position-wise feed-forward network

和 encoder 一样，上面三个部分的每一个部分，都有一个残差连接，后接一个 Layer Normalization。

decoder 和 encoder 不同的地方在 multi-head context-attention mechanism

Attention

这一部分我们在前文中已经提及了，就不多说了，Attention 如果用一句话来描述，那就是 encoder 层的输出经过加权平均后再输入到 decoder 层中。它主要应用在 seq2seq 模型中，这个加权可以用矩阵来表示，也叫 Attention 矩阵。它表示对于某个时刻的输出 y，它在输入 x 上各个部分的注意力。这个注意力就是我们刚才说到的加权。

Attention 又分为很多种，其中两种比较典型的有加性 Attention 和乘性 Attention。加性 Attention 对于输入的隐状态 $h_t$ 和输出的隐状态 $s_t$ 直接做 concat 操作，得到$[s_t:h_t]$ ，乘性 Attention 则是对输入和输出做 dot 操作。

在 Google 这篇论文中，使用的 Attention 模型是乘性 Attention。

Self-Attention

上面我们说attention机制的时候，都会说到两个隐状态，分别是 $h_i$ 和 $s_t$。前者是输入序列第 i个位置产生的隐状态，后者是输出序列在第 t 个位置产生的隐状态。所谓 self-attention 实际上就是，输出序列就是输入序列。因而自己计算自己的 attention 得分。

这里我们在上面也已经提及了，就不细说了。

Context-Attention

context-attention 是 encoder 和 decoder 之间的 attention，是两个不同序列之间的attention，与来源于自身的 self-attention 相区别。

不管是哪种 attention，我们在计算 attention 权重的时候，可以选择很多方式，常用的方法有

• additive attention
• local-base
• general
• dot-product
• scaled dot-product

Transformer模型采用的是最后一种：scaled dot-product attention。

Scaled Dot-Product Attention

那么什么是 scaled dot-product attention 呢？

Google 在论文中对 Attention 机制这么来描述：

An attention function can be described as a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility of the query with the corresponding key.

通过 query 和 key 的相似性程度来确定 value 的权重分布。论文中的公式长下面这个样子：

$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$

scaled dot-product attention 和 dot-product attention 唯一的区别就是，scaled dot-product attention 有一个缩放因子， 叫

$\frac{1}{\sqrt{d_k}}$。$d_k$ 表示 Key 的维度，默认用 64。

论文里对于 $d_k$ 的作用这么来解释：对于 $d_k$ 很大的时候，点积得到的结果维度很大，使得结果处于softmax函数梯度很小的区域。这时候除以一个缩放因子，可以一定程度上减缓这种情况。

scaled dot-product attention 的结构图如下所示。

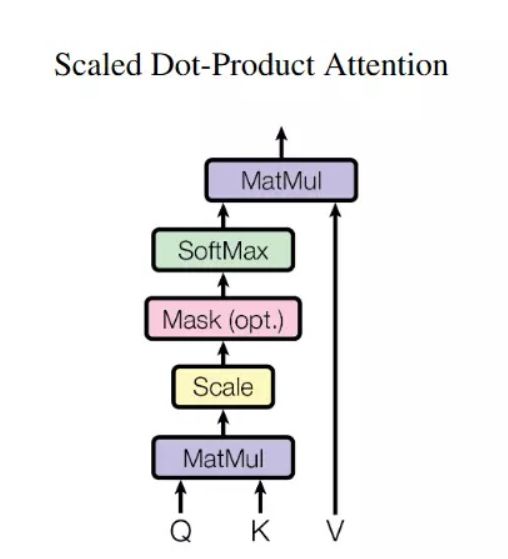
现在来说下 K、Q、V 分别代表什么。当然我们在上文的Self-attention is all you need中已经说明了，相信你也应该理解了它们的含义，但是在Transformer的完整架构中，还存在一些处理的细节，请看完下面的内容：

• 在 encoder 的 self-attention 中，Q、K、V 都来自同一个地方，它们是上一层 encoder 的输出。对于第一层 encoder，它们就是 word embedding 和 positional encoding 相加得到的输入。
• 在 decoder 的 self-attention 中，Q、K、V 也是自于同一个地方，它们是上一层 decoder 的输出。对于第一层 decoder，同样也是 word embedding 和 positional encoding 相加得到的输入。但是对于 decoder，我们不希望它能获得下一个 time step (即将来的信息，不想让他看到它要预测的信息)，因此我们需要进行 sequence masking。
• 在 encoder-decoder attention 中，Q 来自于 decoder 的上一层的输出，K 和 V 来自于 encoder 的输出，K 和 V 是一样的。
• Q、K、V 的维度都是一样的，分别用 $d_Q$,$d_K$和$d_V$来表示

目前可能描述有有点抽象，不容易理解。结合一些应用来说，比如，如果是在自动问答任务中的话，Q 可以代表答案的词向量序列，取 K = V 为问题的词向量序列，那么输出就是所谓的 Aligned Question Embedding。

Google 论文的主要贡献之一是它表明了内部注意力在机器翻译 (甚至是一般的Seq2Seq任务）的序列编码上是相当重要的，而之前关于 Seq2Seq 的研究基本都只是把注意力机制用在解码端。

Scaled Dot-Product Attention 代码实现

import torch
import torch.nn as nn
import torch.functional as F
import numpy as np

class ScaledDotProductAttention(nn.Module):
    """Scaled dot-product attention mechanism."""

    def __init__(self, attention_dropout=0.0):
        super(ScaledDotProductAttention, self).__init__()
        self.dropout = nn.Dropout(attention_dropout)
        self.softmax = nn.Softmax(dim=2)

    def forward(self, q, k, v, scale=None, attn_mask=None):
        """
        前向传播.
        Args:
        	q: Queries张量，形状为[B, L_q, D_q]
        	k: Keys张量，形状为[B, L_k, D_k]
        	v: Values张量，形状为[B, L_v, D_v]，一般来说就是k
        	scale: 缩放因子，一个浮点标量
        	attn_mask: Masking张量，形状为[B, L_q, L_k]

        Returns:
        	上下文张量和attention张量
        """
        attention = torch.bmm(q, k.transpose(1, 2))
        if scale:
            attention = attention * scale
        if attn_mask:
            # 给需要 mask 的地方设置一个负无穷
            attention = attention.masked_fill_(attn_mask, -np.inf)
	# 计算softmax
        attention = self.softmax(attention)
	# 添加dropout
        attention = self.dropout(attention)
	# 和V做点积
        context = torch.bmm(attention, v)
        return context, attention

Multi-head attention 代码实现

在上文中，我们已经详细说过Multi-head attention了，因此这里就不再陈述了，我们仅仅给出代码实现。

class MultiHeadAttention(nn.Module):

    def __init__(self, model_dim=512, num_heads=8, dropout=0.0):
        super(MultiHeadAttention, self).__init__()

        self.dim_per_head = model_dim // num_heads
        self.num_heads = num_heads
        self.linear_k = nn.Linear(model_dim, self.dim_per_head * num_heads)
        self.linear_v = nn.Linear(model_dim, self.dim_per_head * num_heads)
        self.linear_q = nn.Linear(model_dim, self.dim_per_head * num_heads)

        self.dot_product_attention = ScaledDotProductAttention(dropout)
        self.linear_final = nn.Linear(model_dim, model_dim)
        self.dropout = nn.Dropout(dropout)
	
        # multi-head attention之后需要做layer norm
        self.layer_norm = nn.LayerNorm(model_dim)

    def forward(self, key, value, query, attn_mask=None):
	# 残差连接
        residual = query
        dim_per_head = self.dim_per_head
        num_heads = self.num_heads
        batch_size = key.size(0)

        # linear projection
        key = self.linear_k(key)
        value = self.linear_v(value)
        query = self.linear_q(query)

        # split by heads
        key = key.view(batch_size * num_heads, -1, dim_per_head)
        value = value.view(batch_size * num_heads, -1, dim_per_head)
        query = query.view(batch_size * num_heads, -1, dim_per_head)

        if attn_mask:
            attn_mask = attn_mask.repeat(num_heads, 1, 1)

        # scaled dot product attention
        scale = (key.size(-1)) ** -0.5
        context, attention = self.dot_product_attention(
          query, key, value, scale, attn_mask)

        # concat heads
        context = context.view(batch_size, -1, dim_per_head * num_heads)

        # final linear projection
        output = self.linear_final(context)

        # dropout
        output = self.dropout(output)

        # add residual and norm layer
        output = self.layer_norm(residual + output)

        return output, attention

代码中用到了residual connect和 Layer normalization，我们接下来就来讲讲。

Resnet

先抛出一个常规的神经网络结构，如上图所示。

和常规的神经网络结构不同的是，ResNet 引入了残差网络结构(一个shortcht)，通过残差网络，可以把网络层弄的很深，据说可以达到了1000多层，最终的网络分类的效果也是非常好，残差网络的基本结构如上图所示。

通过增加一个 shortcut(也称恒等映射)，而不是简单的堆叠网络层，将原始所需要学习的函数 $H(x)$ 转换成 $F(x)+x$ 。这样可以解决网络由于很深出现梯度消失的问题，从而可以把网络做的很深。

这里我们就不深入了，想了解更多的请看这篇文章： 详解ResNet(深度残差网络)

Layer normalization

Normalization 有很多种，但是它们都有一个共同的目的，那就是把输入转化成均值为 0 方差为 1 的数据。我们在把数据送入激活函数之前进行 normalization（归一化），因为我们不希望输入数据落在激活函数的饱和区。

说到 normalization，那就肯定得提到 Batch Normalization。

BN 的主要思想就是：在每一层的每一批数据上进行归一化。我们可能会对输入数据进行归一化，但是经过该网络层的作用后，我们的数据已经不再是归一化的了。随着这种情况的发展，数据的偏差越来越大，我的反向传播需要考虑到这些大的偏差，这就迫使我们只能使用较小的学习率来防止梯度消失或者梯度爆炸。

BN 的具体做法就是对每一小批数据，在批这个方向上做归一化。如下图所示：

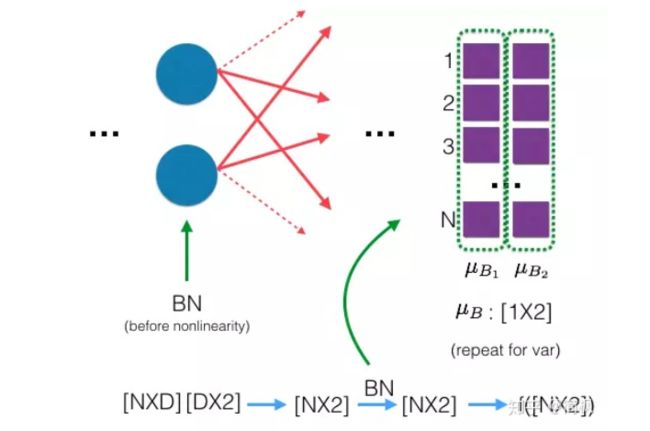
可以看到，右半边求均值是沿着数据 batch N 的方向进行的！

Batch normalization 的计算公式如下：

$$BN(x_i)=\alpha \times \frac{x_i-u_b}{\sqrt{{\sigma }_B^2+ϵ}}+\beta$$

那么什么是 Layer normalization 呢？它也是归一化数据的一种方式，不过 LN 是在每一个样本上计算均值和方差，而不是 BN 那种在批方向计算均值和方差！

下面是 LN 的示意图：

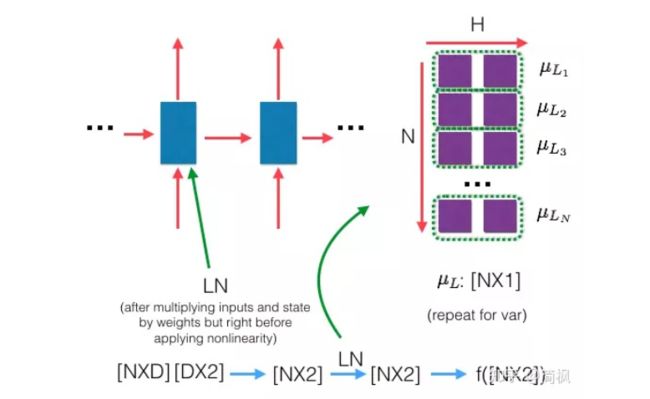
和上面的 BN 示意图一比较就可以看出二者的区别啦！

下面看一下 LN 的公式：

$$LN(x_i)=\alpha \times \frac{x_i-u_L}{\sqrt{{\sigma }_L^2+ϵ}}+\beta$$

Mask

mask 表示掩码，它对某些值进行掩盖，使其在参数更新时不产生效果。Transformer 模型里面涉及两种 mask，分别是 padding mask 和 sequence mask。

其中，padding mask 在所有的 scaled dot-product attention 里面都需要用到，而 sequence mask 只有在 decoder 的 self-attention 里面用到。

Padding Mask

什么是 padding mask 呢？因为每个批次输入序列长度是不一样的也就是说，我们要对输入序列进行对齐。具体来说，就是给在较短的序列后面填充 0。因为这些填充的位置，其实是没什么意义的，所以我们的 attention 机制不应该把注意力放在这些位置上，所以我们需要进行一些处理。

具体的做法是，把这些位置的值加上一个非常大的负数(负无穷)，这样的话，经过 softmax，这些位置的概率就会接近0！

而我们的 padding mask 实际上是一个张量，每个值都是一个 Boolean，值为 false 的地方就是我们要进行处理的地方。

实现：

def padding_mask(seq_k, seq_q):
    # seq_k 和 seq_q 的形状都是 [B,L]
    len_q = seq_q.size(1)
    # `PAD` is 0
    pad_mask = seq_k.eq(0)
    pad_mask = pad_mask.unsqueeze(1).expand(-1, len_q, -1)  # shape [B, L_q, L_k]
    return pad_mask

Sequence mask

文章前面也提到，sequence mask 是为了使得 decoder 不能看见未来的信息。也就是对于一个序列，在 time_step 为 t 的时刻，我们的解码输出应该只能依赖于 t 时刻之前的输出，而不能依赖 t 之后的输出。因此我们需要想一个办法，把 t 之后的信息给隐藏起来。

那么具体怎么做呢？也很简单：产生一个上三角矩阵，上三角的值全为 1，下三角的值权威0，对角线也是 0。把这个矩阵作用在每一个序列上，就可以达到我们的目的啦。

具体的代码实现如下：

def sequence_mask(seq):
    batch_size, seq_len = seq.size()
    mask = torch.triu(torch.ones((seq_len, seq_len), dtype=torch.uint8),
                    diagonal=1)
    mask = mask.unsqueeze(0).expand(batch_size, -1, -1)  # [B, L, L]
    return mask

效果如下，

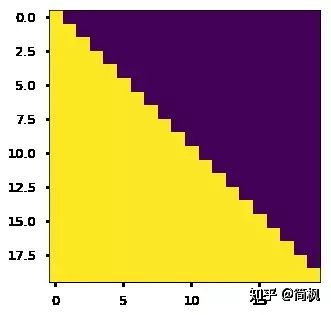
• 对于 decoder 的 self-attention，里面使用到的 scaled dot-product attention，同时需要padding mask 和 sequence mask 作为 attn_mask，具体实现就是两个 mask 相加作为attn_mask。
• 其他情况，attn_mask 一律等于 padding mask。

Positional Embedding

现在的 Transformer 架构还没有提取序列顺序的信息，这个信息对于序列而言非常重要，如果缺失了这个信息，可能我们的结果就是：所有词语都对了，但是无法组成有意义的语句。

为了解决这个问题。论文使用了 Positional Embedding：对序列中的词语出现的位置进行编码。

这一部分，我们上面已经仔细介绍过了，就不再细说了,这里仅给出实现。

class PositionalEncoding(nn.Module):
    
    def __init__(self, d_model, max_seq_len):
        """初始化。
        Args:
            d_model: 一个标量。模型的维度，论文默认是512
            max_seq_len: 一个标量。文本序列的最大长度
        """
        super(PositionalEncoding, self).__init__()
        
        # 根据论文给的公式，构造出PE矩阵
        position_encoding = np.array([
          [pos / np.power(10000, 2.0 * (j // 2) / d_model) for j in range(d_model)]
          for pos in range(max_seq_len)])
        # 偶数列使用sin，奇数列使用cos
        position_encoding[:, 0::2] = np.sin(position_encoding[:, 0::2])
        position_encoding[:, 1::2] = np.cos(position_encoding[:, 1::2])

        # 在PE矩阵的第一行，加上一行全是0的向量，代表这`PAD`的positional encoding
        # 在word embedding中也经常会加上`UNK`，代表位置单词的word embedding，两者十分类似
        # 那么为什么需要这个额外的PAD的编码呢？很简单，因为文本序列的长度不一，我们需要对齐，
        # 短的序列我们使用0在结尾补全，我们也需要这些补全位置的编码，也就是`PAD`对应的位置编码
        pad_row = torch.zeros([1, d_model])
        position_encoding = torch.cat((pad_row, position_encoding))
        
        # 嵌入操作，+1是因为增加了`PAD`这个补全位置的编码，
        # Word embedding中如果词典增加`UNK`，我们也需要+1。看吧，两者十分相似
        self.position_encoding = nn.Embedding(max_seq_len + 1, d_model)
        self.position_encoding.weight = nn.Parameter(position_encoding,
                                                     requires_grad=False)
    def forward(self, input_len):
        """神经网络的前向传播。

        Args:
          input_len: 一个张量，形状为[BATCH_SIZE, 1]。每一个张量的值代表这一批文本序列中对应的长度。

        Returns:
          返回这一批序列的位置编码，进行了对齐。
        """
        
        # 找出这一批序列的最大长度
        max_len = torch.max(input_len)
        tensor = torch.cuda.LongTensor if input_len.is_cuda else torch.LongTensor
        # 对每一个序列的位置进行对齐，在原序列位置的后面补上0
        # 这里range从1开始也是因为要避开PAD(0)的位置
        input_pos = tensor(
          [list(range(1, len + 1)) + [0] * (max_len - len) for len in input_len])
        return self.position_encoding(input_pos)

Position-wise Feed-Forward network

这是一个全连接网络，包含两个线性变换和一个非线性函数(实际上就是 ReLU)。公式如下

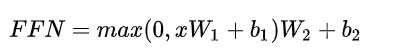
这个线性变换在不同的位置都表现地一样，并且在不同的层之间使用不同的参数。

这里实现上用到了两个一维卷积。

实现如下:

class PositionalWiseFeedForward(nn.Module):

    def __init__(self, model_dim=512, ffn_dim=2048, dropout=0.0):
        super(PositionalWiseFeedForward, self).__init__()
        self.w1 = nn.Conv1d(model_dim, ffn_dim, 1)
        self.w2 = nn.Conv1d(ffn_dim, model_dim, 1)
        self.dropout = nn.Dropout(dropout)
        self.layer_norm = nn.LayerNorm(model_dim)

    def forward(self, x):
        output = x.transpose(1, 2)
        output = self.w2(F.relu(self.w1(output)))
        output = self.dropout(output.transpose(1, 2))

        # add residual and norm layer
        output = self.layer_norm(x + output)
        return output

Transformer的实现

现在可以开始完成 Transformer 模型的构建了，encoder 端和 decoder 端分别都有 6 层，实现如下：

首先是 encoder 端：

class EncoderLayer(nn.Module):
	"""Encoder的一层。"""

    def __init__(self, model_dim=512, num_heads=8, ffn_dim=2048, dropout=0.0):
        super(EncoderLayer, self).__init__()

        self.attention = MultiHeadAttention(model_dim, num_heads, dropout)
        self.feed_forward = PositionalWiseFeedForward(model_dim, ffn_dim, dropout)

    def forward(self, inputs, attn_mask=None):

        # self attention
        context, attention = self.attention(inputs, inputs, inputs, padding_mask)

        # feed forward network
        output = self.feed_forward(context)

        return output, attention


class Encoder(nn.Module):
	"""多层EncoderLayer组成Encoder。"""

    def __init__(self,
               vocab_size,
               max_seq_len,
               num_layers=6,
               model_dim=512,
               num_heads=8,
               ffn_dim=2048,
               dropout=0.0):
        super(Encoder, self).__init__()

        self.encoder_layers = nn.ModuleList(
          [EncoderLayer(model_dim, num_heads, ffn_dim, dropout) for _ in
           range(num_layers)])

        self.seq_embedding = nn.Embedding(vocab_size + 1, model_dim, padding_idx=0)
        self.pos_embedding = PositionalEncoding(model_dim, max_seq_len)

    def forward(self, inputs, inputs_len):
        output = self.seq_embedding(inputs)
        output += self.pos_embedding(inputs_len)

        self_attention_mask = padding_mask(inputs, inputs)

        attentions = []
        for encoder in self.encoder_layers:
            output, attention = encoder(output, self_attention_mask)
            attentions.append(attention)

        return output, attentions

然后是 Decoder 端：

class DecoderLayer(nn.Module):

    def __init__(self, model_dim, num_heads=8, ffn_dim=2048, dropout=0.0):
        super(DecoderLayer, self).__init__()

        self.attention = MultiHeadAttention(model_dim, num_heads, dropout)
        self.feed_forward = PositionalWiseFeedForward(model_dim, ffn_dim, dropout)

    def forward(self,
              dec_inputs,
              enc_outputs,
              self_attn_mask=None,
              context_attn_mask=None):
        # self attention, all inputs are decoder inputs
        dec_output, self_attention = self.attention(
          dec_inputs, dec_inputs, dec_inputs, self_attn_mask)

        # context attention
        # query is decoder's outputs, key and value are encoder's inputs
        dec_output, context_attention = self.attention(
          enc_outputs, enc_outputs, dec_output, context_attn_mask)

        # decoder's output, or context
        dec_output = self.feed_forward(dec_output)

        return dec_output, self_attention, context_attention


class Decoder(nn.Module):

    def __init__(self,
               vocab_size,
               max_seq_len,
               num_layers=6,
               model_dim=512,
               num_heads=8,
               ffn_dim=2048,
               dropout=0.0):
        super(Decoder, self).__init__()

        self.num_layers = num_layers

        self.decoder_layers = nn.ModuleList(
          [DecoderLayer(model_dim, num_heads, ffn_dim, dropout) for _ in
           range(num_layers)])

        self.seq_embedding = nn.Embedding(vocab_size + 1, model_dim, padding_idx=0)
        self.pos_embedding = PositionalEncoding(model_dim, max_seq_len)

    def forward(self, inputs, inputs_len, enc_output, context_attn_mask=None):
        output = self.seq_embedding(inputs)
        output += self.pos_embedding(inputs_len)

        self_attention_padding_mask = padding_mask(inputs, inputs)
        seq_mask = sequence_mask(inputs)
        self_attn_mask = torch.gt((self_attention_padding_mask + seq_mask), 0)

        self_attentions = []
        context_attentions = []
        for decoder in self.decoder_layers:
            output, self_attn, context_attn = decoder(
            output, enc_output, self_attn_mask, context_attn_mask)
            self_attentions.append(self_attn)
            context_attentions.append(context_attn)

        return output, self_attentions, context_attentions


组合一下，就是 Transformer 模型。

class Transformer(nn.Module):

    def __init__(self,
               src_vocab_size,
               src_max_len,
               tgt_vocab_size,
               tgt_max_len,
               num_layers=6,
               model_dim=512,
               num_heads=8,
               ffn_dim=2048,
               dropout=0.2):
        super(Transformer, self).__init__()

        self.encoder = Encoder(src_vocab_size, src_max_len, num_layers, model_dim,
                               num_heads, ffn_dim, dropout)
        self.decoder = Decoder(tgt_vocab_size, tgt_max_len, num_layers, model_dim,
                               num_heads, ffn_dim, dropout)

        self.linear = nn.Linear(model_dim, tgt_vocab_size, bias=False)
        self.softmax = nn.Softmax(dim=2)

    def forward(self, src_seq, src_len, tgt_seq, tgt_len):
        context_attn_mask = padding_mask(tgt_seq, src_seq)

        output, enc_self_attn = self.encoder(src_seq, src_len)

        output, dec_self_attn, ctx_attn = self.decoder(
          tgt_seq, tgt_len, output, context_attn_mask)

        output = self.linear(output)
        output = self.softmax(output)

        return output, enc_self_attn, dec_self_attn, ctx_attn

针对Transformer的三个疑惑

我在学习的时候，其实还是比较顺的，但是还是有三个疑问不得解，查阅了相关资料后，基本有了了解。

• 疑惑一：Transformer的Decoder的输入输出都是什么？
• 疑问二：Shifted Right到底是什么？
• 疑惑三：Transformer里decoder为什么还需要seq mask？

疑惑一：Transformer的Decoder的输入输出都是什么？

以翻译为例：

• 输入：我爱中国
• 输出： I Love China

因为输入（“我爱中国”）在Encoder中进行了编码，这里我们具体讨论Decoder的操作，也就是如何得到输出（“L Love China”）的过程。

Decoder执行步骤

Time Step 1

• • 初始输入： 起始符 + Positional Encoding（位置编码）
  • 中间输入：（我爱中国）Encoder Embedding
  • 最终输出：产生预测“I”

Time Step 2

• • 初始输入：起始符 + “I”+ Positonal Encoding
  • 中间输入：（我爱中国）Encoder Embedding
  • 最终输出：产生预测“Love”

Time Step 3

• • 初始输入：起始符 + “I”+ “Love”+ Positonal Encoding
  • 中间输入：（我爱中国）Encoder Embedding
  • 最终输出：产生预测“China”

【图示】

疑惑二：Shifted Right到底是什么？

操作：整体右移一位（Shifted Right）

细心的同学会发现论文在Decoder的输入上，对Outputs有Shifted Right操作。

Shifted Right 实质上是给输出添加起始符/结束符，方便预测第一个Token/结束预测过程。

正常的输出序列位置关系如下：

• 0-“I”
• 1-“Love”
• 2-“China”

但在执行的过程中，我们在初始输出中添加了起始符，相当于将输出整体右移一位（Shifted Right），所以输出序列变成如下情况：

• 0-【起始符】
• 1-“I”
• 2-“Love”
• 3-“China”

这样我们就可以通过起始符预测“I”，也就是通过起始符预测实际的第一个输出。

上面两个疑惑的总结

Transformer Decoder的输入：

• 初始输入：前一时刻Decoder输入+前一时刻Decoder的预测结果 + Positional Encoding
• 中间输入：Encoder Embedding
• Shifted Right：在输出前添加起始符，方便预测第一个Token

疑惑三：Transformer里decoder为什么还需要seq mask？

Transformer在训练的时候是并行执行的，所以在decoder的第一个sublayer里需要seq mask，其目的就是为了在预测未来数据时把这些未来的数据屏蔽掉，防止数据泄露。如果我们非要去串行执行training，seq mask其实就不需要了。比如说我们用transformer做NMT，训练数据里有一个sample是I love China -->我爱中国。利用串行的思维来想，在训练过程中，我们会

1. 把I love China输入到encoder里去，利用top encoder最终输出的tensor (size: 1X3X512，假设我们采用的embedding长度为512，而且batch size = 1)作为decoder里每一层用到的k和v；

2. 将作为decoder的输入，将decoder最终的输出和‘我’做cross entropy计算error。

3. 将，我作为decoder的输入，将decoder最终:输出的最后一个prob. vector和‘爱’做cross entropy计算error。

4. 将，我，爱 作为decoder的输入，将decoder最终的输出的最后一个prob. vector和‘中’做cross entropy计算error。

5. 将，我，爱，中 作为decoder的输入，将decoder最终的输出的最后一个prob. vector和‘国’做cross entropy计算error。

6. 将，我，爱，中，国 作为decoder的输入，将decoder最终的输出的最后一个prob. vector和做cross entropy计算error。

2-6里都可以不用seq mask。

而在transformer实际的training过程中，我们是并行地将2-6在一步中完成，即

7. 将，我，爱，中，国 作为decoder的输入，将decoder最终输出的5个prob. vector和我，爱，中，国，分别做cross entropy计算error。

比如要想在7中计算第一个prob. vector的整个过程中，都不用到‘我’及其后面字的信息，就必需seq mask。对所有位置的输入，情况都是如此。

但是，仔细想想，7虽然包括了2-6，不过有一点区别。比如对3来说，我们是可以不用seq mask的，这时 所对应的encoder output是会利用’我’里的信息的；而在并行时，seq mask是必需的，这时所对应的encoder output是不会利用’我’里的信息的。

如此一来，我们可以看到，在transformer训练时，由于是并行计算，decoder的第i个输入只能用到i，i-1，…, 0这些位置上输入的信息；当训练完成后，在实际预测过程中，虽然理论上decoder的第i个输入可以用到所有位置上输入的信息，但是由于模型在训练过程中是按照前述方式训练的，所以继续使用seq mask会和训练方式匹配，得到更好的预测结果。

我感觉从理论上看，按照串行方式1-6来训练并且不用seq mask，我们可以把信息用得更足一些，似乎可能模型的效果会好一点，但是计算效率比transformer的并行训练差太多，最终综合来看应该还是并行的综合效果好。

参考

Attention Is All You Need

图解Transformer（完整版）

[整理] 聊聊 Transformer

Transformer 模型详解

详解Transformer （Attention Is All You Need）

神经机器翻译 之 谷歌 transformer 模型