特征选择过滤法-方差过滤、F检验、互信息法
过滤法
过滤法通常用作预处理步骤,特征选择完全独立于任何机器学习算法。它是根据各种统计检验分数和相关性指标来选择特征。
全部特征--->最佳特征子集--->算法--->模型评估
1.方差过滤 ---VarianceThreshold
这是一个通过特征本身的方差来筛选特征的类。比如一个特征的方差很小,就表示样本在这个特征上基本没有差异,可能特征中的大多数值都一样,甚至整个特征的取值都相同,那么这个特征对于样本区分没有什么作用。所以无论接下来的特征工程要做什么,都要先消除方差为0的特征。VarianceThreshold有重要参数threshold,表示方差的阈值,表示舍弃所有方差小于threshold的特征,不填默认为0,即删除所有记录都相同的特征。方差过滤示例代码如下:
import pandas as pd
data=pd.read_csv(r"F:\sklearn预处理数据集\digit recognizor.csv")
x=data.iloc[:,1:]
y=data.iloc[:,0]
x.shape #(42000, 784) 此数据集有42000行,784个特征
from sklearn.feature_selection import VarianceThreshold
selector=VarianceThreshold() #实例化,不填参数默认方差为0
x_var0=selector.fit_transform(x) #获取删除不合格特征之后的新特征矩阵
#也可以直接写成x=VarianceThreshold().fit_transform(x)
x_var0.shape #(42000, 708)
可以看出,在删除了方差为0的特征之后,依然剩下708个特征,明显还需要做进一步的特征选择,假如这里只想保留一半的特征,那么可以设定一个让特征总数减半的阈值,只要找到特征方差的中位数并设为参数threshold的值。
import numpy as np
x_fsvar=VarianceThreshold(np.median(x.var().values)).fit_transform(x)
x_fsvar.shape
-------------------------------代码分割线----------------------------
(42000, 392)PS:当特征是二分类时,特征的取值就是伯努利随机变量,这些变量的方差可以计算为: Var[X]=p(1-p)。其中X是特征矩阵,p是二分类特征中的一类在这个特征中所占的概率(注:伯努利分布指的是对于随机变量X有, 参数为p(0
假设p=0.8,即二分类特征中某种分类占到80%以上的时候删除特征。
x_bvar=VarianceThreshold(0.8*(1-0.8)).fit_transform(x)
x_bvar.shape
--------------------代码分割线---------------------------
(42000, 685)1.1方差过滤后对模型的影响
为了检验方差过滤后对模型的影响,这里分别用KNN和随机森林两种方法分别在方差过滤前和方差过滤后运行的效果和运行时间的对比。(KNN是K近邻算法中的分类算法,其原理是利用每个样本到其它样本点的距离来判断每个样本点的相似度,然后进行样本分类。KNN必出遍历每个特征和每个样本,因而特征越多,KNN的计算越缓慢)完整代码如下:
#KNN 和 随机森林在不同方差过滤效果下的对比
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.neighbors import KNeighborsClassifier as KNN
from sklearn.model_selection import cross_val_score
import numpy as np
x=data.iloc[:,1:]
y=data.iloc[:,0]
x_fsvar=VarianceThreshold(np.median(x.var().values)).fit_transform(x)
#KNN-方差过滤前效果
cross_val_score(KNN(),x,y,cv=5).mean()
%%timeit #计算代码平均运行时间
cross_val_score(KNN(),x,y,cv=5).mean()
#KNN-方差过滤后效果
cross_val_score(KNN(),x_fsvar,y,cv=5).mean()
%%timeit #计算代码平均运行时间
cross_val_score(KNN(),x_fsvar,y,cv=5).mean()
#随机森林-方差过滤前效果
cross_val_score(RFC(n_estimators=10,random_state=0),x,y,cv=5).mean()
%%timeit #计算代码平均运行时间
cross_val_score(RFC(n_estimators=10,random_state=0),x,y,cv=5).mean()
#随机森林-方差过滤后效果
cross_val_score(RFC(n_estimators=10,random_state=0),x_fsvar,y,cv=5).mean()
%%timeit #计算代码平均运行时间
cross_val_score(RFC(n_estimators=10,random_state=0),x_fsvar,y,cv=5).mean()
-----------------------------------代码分割线---------------------------------------
KNN-方差过滤前效果:0.965857142857143
KNN-方差过滤前时间:34.1 s ± 365 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
KNN-方差过滤后效果:0.966
KNN-方差过滤后时间:27.6 s ± 173 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
随机森林-方差过滤前效果:0.9373571428571429
随机森林-方差过滤前时间:11.5 s ± 305 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
随机森林-方差过滤后效果:0.9390476190476191
随机森林-方差过滤后时间:11.1 s ± 72 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
根据以上结果,可以观察到随机森林的准确率略逊于KNN,但运行时间比KNN短。方差过滤后,随机森林和KNN的准确率都微弱上升 ,随机森林运行时间基本无明显变化,而KNN运行时间明显减少。
Q:为什么随机森林运行如此之快?为什么方差过滤对随机森林没有很大的影响?
A:这是由于两种算法的原理中涉及到的计算量不同。最近邻算法KNN,单棵决策树,支持向量机SVM,神经网络,回归算法,都需要遍历特征或升维来进行运算,所以他们本身的运算量就很大,需要的时间就很长,因此方差过滤这样的特征选择对他们来说尤为重要。但对于不需要遍历特征的算法,比如随机森林,它随机选取特征进行分枝,本身运算就非常快速,因此特征选择对它来说效果并不明显。这其实很容易理解,无论过滤法如何降低特征的数量,随机森林也只会选取固定数量的特征来建模;而最近邻算法就不同了,特征越少,距离计算的维度就越少,模型明显会随着特征的减少而变得轻量。因此,
过滤法的主要对象是:需要遍历特征或升维的算法
过滤法的主要目的是:在维持算法表现的前提下,帮助算法降低计算成本
--------------菜菜机器学习
Q:过滤法对随机森林无效,却对树模型有效?
A: 从算法原理上来说,传统决策树需要遍历所有特征,计算不纯度后进行分枝,而随机森林却是随机抽取进行计算和分枝。因此随机森林的运算更快,过滤法对随机森林无用,对决策树却有用。
在sklearn中,决策树和随机森林都是随机选择特征进行分枝,但决策树在建模过程中随 机抽取的特征数目却远远超过随机森林当中每棵树随机抽取的特征数目(比如对于这个780维的数据,随机森林每棵树只会抽取10-20个特征,而决策树可能会抽取200~400个特征),因此,过滤法对随机森林无用,却对决策树有用。也因此,在sklearn中,随机森林中的每棵树都比单独的一棵决策树简单得多,高维数据下的随机森林的计算比决策树快很多。
--------------菜菜机器学习
| 阈值很小 被过滤掉的特征比较少 |
阈值较大 被过滤掉的特征比较少多 |
|
| 模型表现 | 不会有太大影响 | 可能变得更好,代表被滤掉的特征大部分是噪音;也可能变糟糕,代表被滤掉的特征中很多都是有效特征 |
| 运行时间 | 可能降低模型的运行时间基于方差很小的特征有多少 当方差很小的特征不多时,对模型没有太大影响 |
一定能够降低模型的运行时间,算法在遍历特征时的计算越复杂,运行时间下降得越多 |
在我们的对比中,我们使用的方差阈值是特征方差中的中位数,因此属于阈值比较大,过滤掉的特征比较多的情况。无论是KNN还是随机森林,在过滤掉一般特征之后,模型的精确度都上升了。这说明被我们过滤掉的特征在当前模式下大部分都是噪音,那我们就可以保留这个去掉了一半特征的数据,来为之后的特征选择做准备。当然,如果过滤之后模型的效果变差了,我们就可以认为,被我们过滤掉的特征中有很多都是有效特征,那就应当采取另一种方法进行特征选择。
2.相关性过滤
方差调训完毕后,接下来就考虑相关性了,常用的来评判特征与标签之间的相关性方法有:卡方检验,F检验,互信息法。
2.1卡方过滤
卡方过滤是专门针对离散型标签(即分类问题)的相关性过滤。卡方检验类feature_selection.chi2计算每个非负特征和标签之间的卡方统计量,并依照卡方统计量由高到低为特征排名。再结合feature_selection.SelectKBest 这个可以输入“评分标准”来选出前K个分数最高的特征的类,我们可以借此除去最可能独立于标签,与我们分类目的无关的特征。
另外,如果卡方检验检测到某个特征中所有的值都相同,会提示我们适用方差先进性方差过滤。并且,刚才我们已经验证过,当我们适用方差过滤筛掉一般特征之后,模型的表现是提升的,这里我们使用threshold=中位数时完成的方差过滤来做卡方检验。
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
#卡方检验
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
#假设这里需要300个特征
x_fschi=SelectKBest(chi2,k=300).fit_transform(x_fsvar,y)
x_fschi.shape #(42000, 300)
#验证模型效果
cross_val_score(RFC(n_estimators=10,random_state=0),x_fschi,y,cv=5).mean()
----------------------------------------------------------------------------
0.9344761904761905此时模型的效果降低了,说明在设定k=300的时候删除了与模型相关且有效的特征,我们的k值设置得太小,需要重新调整k值,为了能够选择一个最优的超参数k,在这里可画出学习曲线:
%matplotlib inline
import matplotlib.pyplot as plt
score=[]
for i in range(390,200,-10):
x_fschi=SelectKBest(chi2,k=i).fit_transform(x_fsvar,y)
once=cross_val_score(RFC(n_estimators=10,random_state=0),x_fschi,y,cv=5).mean()
score.append(once)
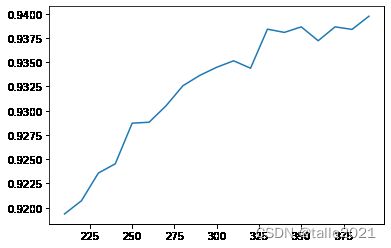
plt.plot(range(390,200,-10),score)
plt.show()
得到的学习曲线如图:
通过这条曲线,可以观察到,随着k值的不断增加,模型的表现不断上升,这说明,k越大越好,数据中所有的特征都是与特征相关的。但是运行这条曲线的时间同样的也是非常长,接下来介绍一种更好的选择k的方法:看p值选择k。
卡方检验的本质是推测两组数据间的差异,期检验的原假设是“两组数据是相互独立的”。卡方检验返回卡方值和p值两个统计量,其中卡方值很难界定有效的范围,而p值,一般使用0.05或0.01作为显著性特征水平,即p值判断的边界
| p值 | <=0.05或0.01 | >0.05或0.01 |
| 数据差异 | 差异不是自然形成的 | 这些差异是很自然的样本误差 |
| 相关性 | 两组数据是相关的 | 两组数据是相互独立的 |
| 原假设 | 拒绝原假设,接受备择假设 | 接受原假设 |
chivalue,pvalues_chi=chi2(x_fsvar,y)
#print("卡方值",chivalue)
#print("p值",pvalues_chi)
#k取多少?我们相要消除所有p值大于设定值,比如0.05或0.01的特征:
k=chivalue.shape[0]-(pvalues_chi>0.05).sum()
print(k) #特征数量减删除的特征数量
---------------------------------------------------------
k=0k=0,说明所有p值都小于0.05,也就是方差过滤已经把所有和标签无关的特征都剔除了,或者中国数据集本身就不含与标签无关的特征。在这种情况下,舍弃任何一个特征,都会舍弃对模型有用的信息,而使模型表现下降。接下来,继续试用其它相关性过滤的方法来验证。
2.2 F检验
F检验,又称ANOVA,方差齐性检验,是用来捕捉每个特征与标签之间的线性关系的过滤方法。F检验既可以做回归,也可以做分类,因此包含faeture_selection.f_classif(F检验分类)和feature_selection.f_regression(F检验回归)两个类。其中F检验分类用于标签是离散型变量的数据,而F检验回归用于标签是连续型变量的数据。
和卡方检验一样,这两个类需要和类SelectKBest连用,并且也可以直接通过输出的统计量来判断设置一个什么样的k合适。F检验在数据服从正态分布时效果会非常稳定,所以在使用F检验过滤时通常会先将数据转化为服从正态分布的方式。
F检验的本质是寻找两组数据之间的线性关系,其原假设是“数据不存在显著的线性关系”。它返回F值和p值两个统计量。和卡方过滤一样,我们希望选取p值小于0.01或0.05的特征,这些特征与标签是显著线性相关的。以F检验为例,继续在数据集上进行特征选择:
#F检验
from sklearn.feature_selection import f_classif
F,pvalues_f=f_classif(x_fsvar,y)
#print("F值",F)
#print("p值",pvalues_f)
k=F.shape[0]-(pvalues_f>0.05).sum()
print(k)
--------------------------------------------
k=0得到的结论和卡方过滤得到的结果一样,没有任何特征的p值大于0.05,所以有特征都与标签相关,因此不需要相关性过滤。
2.3 互信息法
互信息法是用来捕捉每个特征与标签之间的任意关系(包括线性和非线性)的过滤方法。和F检验相似,它既可以做回归,也可以做分类,并且包含两个类feature_selection.mutual_info_classif(互信息分类) feature_selection.mutual_info_regression(互信息回归)。这两个类的用法和参数都和F检验一样,但F检验只能找出线性关系,而互信息法可以找出任意关系。
互信息法不返回F值和p值类似的统计量,它返回“每个特征与目标之间互信息量的估计”,这个估计量在[0,1]之间取值,0表示两个变量相互独立,1则表示两个变量完全相关,以互信息分类为例的代码如下:
#互信息法
from sklearn.feature_selection import mutual_info_classif as MIC
result=MIC(x_fsvar,y) #得到互信息量的估计
#print(result)
(result>0).sum()
-------------------------------------------------------------------
392所有特征的互信息量估计都大于0,因此所有特征都与标签有关。
3.过滤法总结
通常先使用方差过滤,再使用互信息法来捕捉相关性。
| 类 | 说明 | 超参数的选择 |
| VarianceThreshold | 方差过滤,可输入方差阈值,返回方差大于阈值的新特征矩阵 | (学习曲线) |
| SelectKBest | 用来选取K个统计量结果最佳的特征,生成符合统计量要求的新特征矩阵 | |
| chi2 | 卡方检验,专用于分类算法,捕捉相关性 | 追求p小于显著性水平的特征 |
| f_classif | F检验分类,只能捕捉线性相关性 要求数据服从正态分布 |
追求p小于显著性水平的特征 |
| f_regression | F检验回归,只能捕捉线性相关性 要求数据服从正态分布 |
追求p小于显著性水平的特征 |
| mutual_info_classif | 互信息分类,可以捕捉任何相关性 不能用于稀疏矩阵 |
追求互信息大于0的特征 |
| mutual_info_regression | 互信息回归,可以捕捉任何相关性 不能用于稀疏矩阵 |
追求互信息大于0的特征 |