从贝叶斯网络到SLAM
#c 引入
SLAM是一项应用于机器人环境探索的技术。早期的应用实例是NASA的火星车。结合这个应用场景,很容易看出SLAM的作用。火星对于我们是一个未知环境,我们想要知道火星上有什么,那就发射一个带一大堆传感器的机器人过去,通过传感器数据,建立火星表面的地图,并给出机器人在地图中的位置(机器人打开战争迷雾)。

求解SLAM状态估计问题分成2个手段:1.滤波 2.优化
通过贝叶斯网络构建方程,对应于滤波方法。
通过因子图构建方程,对应于优化方法。
早期的SLAM多是基于滤波的。当前流行的则是优化。
这篇博客先介绍贝叶斯网络并回顾必要的概率内容,再讲贝叶斯网络在SLAM中的具体意义。
贝叶斯网络与概率
在一个随机试验中,我们会对多个随机变量产生兴趣。
#e 多维随机变量的例子
- 谈到毕业生的薪水时,我们很感兴趣的两个随机变量是 X 1 X_{1} X1为哪个学校毕业, X 2 X_{2} X2为薪水多少。在这个随机试验里, P ( X 2 = 高薪 ∣ X 1 = 清华大学 ) > P ( X 2 = 高薪 ∣ X 1 = 10422 ) P(X_{2}=高薪|X_{1}=清华大学)>P(X_{2}=高薪|X_{1}=10422) P(X2=高薪∣X1=清华大学)>P(X2=高薪∣X1=10422)。
- 对于身高,以父母身高为 X 1 和 X 2 X_{1}和X_{2} X1和X2,孩子身高为 X 3 X_{3} X3,成长省份为 X 4 X_{4} X4,苹果手机今年的发布价格为 X 5 X_{5} X5,苹果手机的销量为 X 6 X_{6} X6。在这个随机试验里, P ( X 1 = 1.7 , X 2 = 1.7 , X 3 = 1.7 , X 4 = 湖南 , X 5 = 9 k ) = P ( X 1 = 1.7 , X 2 = 1.7 , X 3 = 1.7 , X 4 = 湖南 ) P(X_{1}=1.7,X_{2}=1.7,X_{3}=1.7,X_{4}=湖南,X_{5}=9k)=P(X_{1}=1.7,X_{2}=1.7,X_{3}=1.7,X_{4}=湖南) P(X1=1.7,X2=1.7,X3=1.7,X4=湖南,X5=9k)=P(X1=1.7,X2=1.7,X3=1.7,X4=湖南)。很明显苹果手机的价格和身高这几个随机变量无关。
随机变量之间存在着复杂的关系。从上面的例子看出,我们研究的部分随机变量存在关联,有些不存在关联。直接求解联合概率分布显然是非常复杂的。当我们知道各个随机变量之间的依赖关系时,便可以通过概率图模型降低求解联合分布的难度。随机变量间是有向、无环关系的时候,这种概率图结构就是贝叶斯网络。(无向时为马尔可夫随机场,另一种概率图)
#e 贝叶斯网络的例子
对一个学生能否拿到的薪水进行建模。假设相关的随机变量有5个 X 1 X_{1} X1~ X 5 X_{5} X5分别是
高考成绩、学校招生人数、就读大学、大学成绩、薪水。
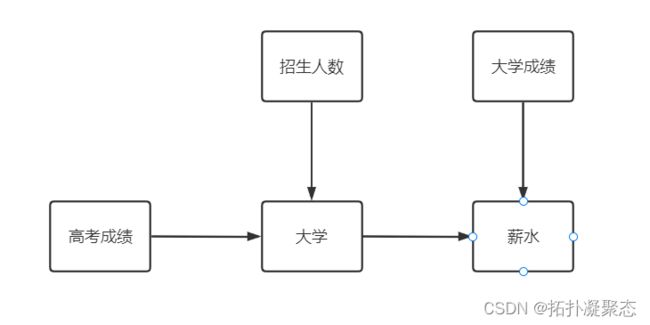
我们关心的是随机变量间的关系,直接用一张图表示出来
显然从图中可以看出各个变量的依赖关系。这张图体现了2个要素:有向、无环。距离一个完整的贝叶斯网络只差一部,那便是求出多维随机变量的分布。
要求分别,那先明确各个变量的取值(或者说给图的节点定义):
- 高考成绩 X 1 X_{1} X1:高分、低分
- 招生人数 X 2 X_{2} X2:多、中、少
- 入读大学 X 3 X_{3} X3:清华大学、北京城市学院
- 大学成绩 X 4 X_{4} X4:高分、普通、低分
- 薪水 X 5 X_{5} X5:高薪、低薪
建立统计模型最终目的是找出随机变量分布 P ( X 1 , X 2 , X 3 , X 4 , X 5 ) P(X_{1},X_{2},X_{3},X_{4},X_{5}) P(X1,X2,X3,X4,X5)。贝叶斯网络的作用,就是简化这个随机变量的表达式。
为了继续推进,插播两个公式
对于随机变量A,B,C:
#d 乘法公式
P ( A , B , C ) = P ( A ) P ( B ∣ A ) P ( C ∣ B , A ) P(A,B,C)=P(A)P(B|A)P(C|B,A) P(A,B,C)=P(A)P(B∣A)P(C∣B,A)
简单说一下怎么来的。
条件概率的定义是 P ( B ∣ A ) = P ( A , B ) P ( A ) P(B|A)=\frac{P(A,B)}{P(A)} P(B∣A)=P(A)P(A,B)。其实就是把右边下面的分母乘到左边。3个事件是2个事件的推广。
#d 条件独立
当A与C无关时:
P ( C ∣ B , A ) = P ( C ∣ B ) P(C|B,A)=P(C|B) P(C∣B,A)=P(C∣B)
比如我们只取招生人数、就读大学、薪水3个变量研究关系。明显 P ( X 5 ∣ X 3 ) = P ( X 5 ∣ X 3 , X 2 ) P(X_{5}|X_{3})=P(X_{5}|X_{3},X_{2}) P(X5∣X3)=P(X5∣X3,X2)。当年学校招生人数和工资没有1点关系,当获取招生人数信息后并不能调整薪水分布的概率空间。
1.我们先套用乘法公式,看看咋个样子。
P ( X 1 , X 2 , X 3 , X 4 , X 5 ) = P ( X 1 ) P ( X 2 , X 3 , X 4 , X 5 ∣ X 1 ) P ( X 1 , X 2 , X 3 , X 4 , X 5 ) = P ( X 1 ) P ( X 2 ∣ X 1 ) P ( X 3 , X 4 , X 5 ∣ X 1 , X 2 ) P ( X 1 , X 2 , X 3 , X 4 , X 5 ) = P ( X 1 ) P ( X 2 ∣ X 1 ) P ( X 3 ∣ X 1 , X 2 ) P ( X 4 , X 5 ∣ X 1 , X 2 , X 3 ) P ( X 1 , X 2 , X 3 , X 4 , X 5 ) = P ( X 1 ) P ( X 2 ∣ X 1 ) P ( X 3 ∣ X 1 , X 2 ) P ( X 4 ∣ X 1 , X 2 , X 3 ) P ( X 5 ∣ X 1 , X 2 , X 3 , X 4 ) P(X_{1},X_{2},X_{3},X_{4},X_{5} )=P(X_{1})P(X_{2},X_{3},X_{4},X_{5}|X_{1}) \newline P(X_{1},X_{2},X_{3},X_{4},X_{5})=P(X_{1})P(X_{2}|X_{1})P(X_{3},X_{4},X_{5}|X_{1},X_{2}) \newline P(X_{1},X_{2},X_{3},X_{4},X_{5})=P(X_{1})P(X_{2}|X_{1})P(X_{3}|X_{1},X_{2})P(X_{4},X_{5}|X_{1},X_{2},X_{3}) \newline P(X_{1},X_{2},X_{3},X_{4},X_{5})=P(X_{1})P(X_{2}|X_{1})P(X_{3}|X_{1},X_{2})P(X_{4}|X_{1},X_{2},X_{3})P(X_{5}|X_{1},X_{2},X_{3},X_{4}) P(X1,X2,X3,X4,X5)=P(X1)P(X2,X3,X4,X5∣X1)P(X1,X2,X3,X4,X5)=P(X1)P(X2∣X1)P(X3,X4,X5∣X1,X2)P(X1,X2,X3,X4,X5)=P(X1)P(X2∣X1)P(X3∣X1,X2)P(X4,X5∣X1,X2,X3)P(X1,X2,X3,X4,X5)=P(X1)P(X2∣X1)P(X3∣X1,X2)P(X4∣X1,X2,X3)P(X5∣X1,X2,X3,X4)
2.我们再接着用条件独立,看看最终形式如何。由上文可知,哪些变量之间存在依赖关系。
P ( X 1 , X 2 , X 3 , X 4 , X 5 ) = P ( X 1 ) P ( X 2 ∣ X 1 ) P ( X 3 ∣ X 1 , X 2 ) P ( X 4 ∣ X 1 , X 2 , X 3 ) P ( X 5 ∣ X 1 , X 2 , X 3 , X 4 ) P ( X 1 , X 2 , X 3 , X 4 , X 5 ) = P ( X 1 ) P ( X 2 ) P ( X 3 ∣ X 1 , X 2 ) P ( X 4 ) P ( X 5 ∣ X 3 , X 4 ) P(X_{1},X_{2},X_{3},X_{4},X_{5})=P(X_{1})P(X_{2}|X_{1})P(X_{3}|X_{1},X_{2})P(X_{4}|X_{1},X_{2},X_{3})P(X_{5}|X_{1},X_{2},X_{3},X_{4}) \newline P(X_{1},X_{2},X_{3},X_{4},X_{5})=P(X_{1})P(X_{2})P(X_{3}|X_{1},X_{2})P(X_{4})P(X_{5}|X_{3},X_{4}) P(X1,X2,X3,X4,X5)=P(X1)P(X2∣X1)P(X3∣X1,X2)P(X4∣X1,X2,X3)P(X5∣X1,X2,X3,X4)P(X1,X2,X3,X4,X5)=P(X1)P(X2)P(X3∣X1,X2)P(X4)P(X5∣X3,X4)
在使用了乘法公式后,每一个节点都会有一大堆与之相关的条件。通过简化,每一项只保留了与之相关的条件随机变量。到这里,已经完成了这个问题的贝叶斯网络。
然后就可以给出贝叶斯网络表示的随机变量数学形式:
P ( X 1 , X 2 , . . . , X N ) = ∏ i N P ( X i ∣ P a r G ( X i ) ) P(X_{1},X_{2},...,X_{N})=\prod_{i}^{N}P(X_{i}|Par_{G}(X_{i})) P(X1,X2,...,XN)=i∏NP(Xi∣ParG(Xi))
每一个 X i X_{i} Xi对应一个图中的节点。先介绍一下 P a r G ( X i ) Par_{G}(X_{i}) ParG(Xi),这个东西就是与 X i X_{i} Xi这个节点相关的父节点随机变量。在我们上文的例子中,对于 X 5 X_{5} X5节点, P a r G ( X 5 ) Par_{G}(X_{5}) ParG(X5)就是 X 3 , X 4 X_{3},X_{4} X3,X4,对应于公式末尾那一项。
当我们知道各个变量依赖关系,也就是构建出图时,我们不再需要按照乘法公式+条件概率一个一个的套用。直接应用上面这个公式就可以列出概率的分布,非常方便。
SLAM中的贝叶斯网络
介绍上面那个贝叶斯网络其实别有用意。问题来了,SLAM中究竟是如何使用贝叶斯网络的?
首先,我们有机器人的任务有两个。同时定位与建图,无非就是预测机器人的位置,以及预测环境中障碍物的位置呗。so,我们得出两个随机变量机器人状态以及障碍物(又称为路标、Landmark)状态。
机器人状态(每一个随机变量代表机器人每一次的移动)
X = { X 1 , X 2 , X 3 , . . . } X= \left \{ X_{1},X_{2},X_{3},...\right \} X={X1,X2,X3,...}
路标状态
L = { L 1 , L 2 , L 3 , . . . } L= \left \{ L_{1},L_{2},L_{3},...\right \} L={L1,L2,L3,...}
既然是随机变量,已经暗含了我们不可能精确求出其大小的事实。我们无法直接求得这俩随机变量,但可以通过求与之相关的随机变量,获取一个更精确的概率分布。
控制信号
U = { U 1 , U 2 , U 3 , . . . } U= \left \{ U_{1},U_{2},U_{3},...\right \} U={U1,U2,U3,...}
测量信号
Z = { Z 1 , Z 2 , Z 3 , . . . } Z= \left \{ Z_{1},Z_{2},Z_{3},...\right \} Z={Z1,Z2,Z3,...}
控制信号是可以直接读的,比如电机编码器,主要是针对机器人本体。当然,无论何种形式,就是你下达的指令,让机器人挪动多少。理想情况下,你的控制信号 U U U输入多少,你的 X X X就变化多少。真实世界是存在噪声的。来自执行器的噪声信号加上输入信号,可能让你机器人移动了更远或者更少的距离。这个关系可以这样表示:
X k = f ( X k − 1 , U k , w k ) X_{k}=f(X_{k-1},U_{k},w_{k}) Xk=f(Xk−1,Uk,wk)
这又被称作SLAM的运动方程。( w k w_{k} wk是噪声信号)可以看出, X k X_{k} Xk仅仅和另2个随机变量有关。这两个变量就是该变量节点的父节点。取出网络中的一小部分,长下面这样。
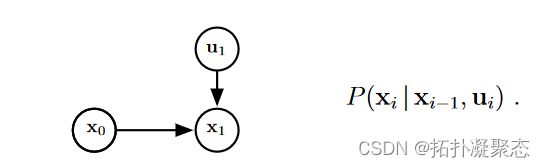
附注解释一下, X 0 X_{0} X0被当作上个例子中的高考成绩, U 1 U_{1} U1被当作招生人数。进而估计下一个位姿 X 1 X_{1} X1对应于例子中的大学。
测量信号就是对路标的观测,一般来自激光雷达或者相机,主要是针对环境。其形式也是多种多样,可以是点云、也或者是彩色图像、深度图像。就拿普通的相机来说,路标 L j L_{j} Lj是一个随机变量, Z k , j Z_{k,j} Zk,j就是当前捕获的图像。
Z k , j = h ( L j , X k , v k , j ) Z_{k,j}=h(L_{j},X_{k},v_{k,j}) Zk,j=h(Lj,Xk,vk,j)
这又被称作SLAM的观测方程。

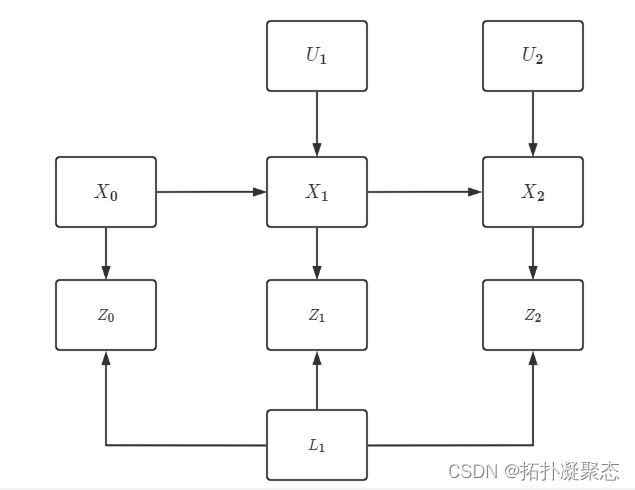
有了这俩东西就好办了,我们就可以搭出一个完整的网络。
通过贝叶斯网络,我们可以得到SLAM里概率分布的表达式如下
P ( X 0 , X 1 , X 2 , L 1 , U 1 , U 2 , Z 0 , Z 1 , Z 2 ) → P ( X 0 ) ∏ i = 1 M P ( X i ∣ X i − 1 , U i ) ∏ k = 1 K P ( Z k ∣ X i , L k ) P(X_{0},X_{1},X_{2},L_{1},U_{1},U_{2},Z_{0},Z_{1},Z_{2})\to P(X_{0})\prod_{i=1}^{M}P(X_{i}|X_{i-1},U_{i})\prod_{k=1}^{K}P(Z_{k}|X_{i},L_{k}) P(X0,X1,X2,L1,U1,U2,Z0,Z1,Z2)→P(X0)i=1∏MP(Xi∣Xi−1,Ui)k=1∏KP(Zk∣Xi,Lk)
打公式太费劲,就不展开了。建立了贝叶斯网络后,我们的任务便是明确的。那就是找到一组随机变量,使得这个概率可能性最大!
( X 0 , X 1 , X 2 , L 1 ) = a r g max X 0 , X 1 , X 2 , L 1 P ( X 0 ) ∏ i = 1 M P ( X i ∣ X i − 1 , U i ) ∏ k = 1 K P ( Z k ∣ X i , L k ) (X_{0},X_{1},X_{2},L_{1})=arg\max_{X_{0},X_{1},X_{2},L_{1}} P(X_{0})\prod_{i=1}^{M}P(X_{i}|X_{i-1},U_{i})\prod_{k=1}^{K}P(Z_{k}|X_{i},L_{k}) (X0,X1,X2,L1)=argX0,X1,X2,L1maxP(X0)i=1∏MP(Xi∣Xi−1,Ui)k=1∏KP(Zk∣Xi,Lk)
Reference
- SLAM course (强推,作者的主页上有一些资料可以直接下载。后面这些公式推导参考了不少内容。)
- 视觉SLAM十四讲
- 链式法则,其实就是乘法公式
- 概率图
- 贝叶斯网络,这个讲的不戳,而且比较短