计算机视觉之SSD改进版本(平滑L1范数损失与焦点损失)《4》
在 计算机视觉之单发多框检测(Single Shot MultiBox Detector)模型《3》中我们使用到的是L1范数损失,L1范数损失也叫做平均绝对误差(MAE),目标值与预测值之差的绝对值的和,表示的是预测值的平均误差幅度。它的缺点就是0点附近不能求导,不方便求解,而且不光滑,网络也不是很稳定,所以我们设计一个在0点附近使用一个平方函数,让它显得很平滑,这里通过一个超参数![]() 来控制平滑区域。
来控制平滑区域。
平滑L1范数损失(Smooth_L1)
我们可以先看下数学公式:
代码实现很简单,我们看个小栗子:
from mxnet import nd
print(nd.smooth_l1(nd.array([-1,0.1, 0.5, 1, 2, 3, 4]), scalar=1))
#[0.5 0.005 0.125 0.5 1.5 2.5 3.5 ]这里的sigma是参数scalar,可以看出对输入做了分两步讨论并计算的。我们来画图更直观的看下:
sigmas = [10, 1, 0.5]
lines = ['-', '--', '-.']
x = nd.arange(-2, 2, 0.1)
d2l.set_figsize()
for l, s in zip(lines, sigmas):
y = nd.smooth_l1(x, scalar=s)
d2l.plt.plot(x.asnumpy(),y.asnumpy(),l,label='sigma=%.1f'%s)
d2l.plt.legend()
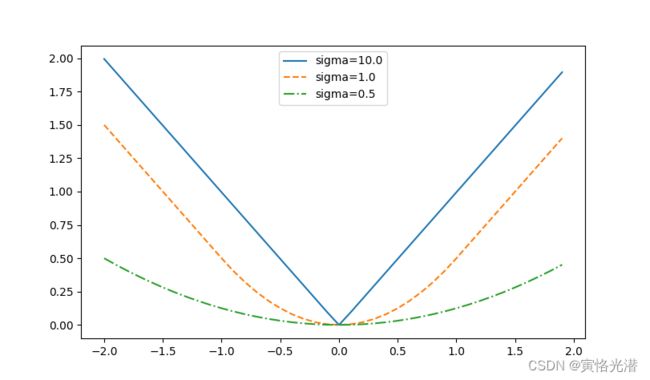
d2l.plt.show()可以看到这个超参数sigma很大的时候,图形就是这个L1范数损失了,在零点显得很尖锐,当sigma比较小的时候,这个图形就显得很平滑。
另外:L2范数损失函数,也叫最小平方误差(LSE),就是目标值与预测值之差的平方和最小化。一般的回归问题用这个比较多,但是有了平方,你想下,这个误差就平方了,也就是说模型对于这个样本的敏感性高很多了,相对来说不是很稳定,所以L1范数损失的鲁棒性比L2范数损失要好点。
我们来看下在MXNet中的实现:
class SmoothL1Loss(gluon.loss.Loss):
def __init__(self, batch_axis=0, **kwargs):
super(SmoothL1Loss, self).__init__(None, batch_axis, **kwargs)
def hybrid_forward(self, F, output, label, mask):
loss = F.smooth_l1((output - label) * mask, scalar=1.0)
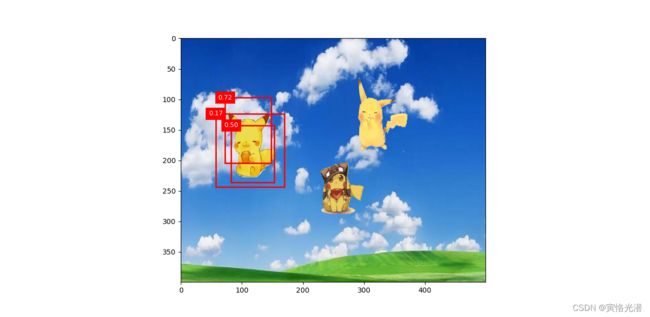
return F.mean(loss, self._batch_axis, exclude=True)然后应用到皮卡丘的检测中,我们发现图中的检测框要精细点了,多了几个是吧,虽然只检测到了一个皮卡丘,原因可能是迭代次数比较少的问题,使用的损失函数比较平滑的缘故,不像那个L1范数损失那么强烈。
焦点损失(Focal Loss,FL)
我们除了使用交叉熵损失:设真实类别j的预测概率是![]() ,交叉熵损失为:
,交叉熵损失为:![]() 。
。
还可以使用焦点损失(focus loss):给定正的超参数γ和α,该损失函数的定义为:
![]()
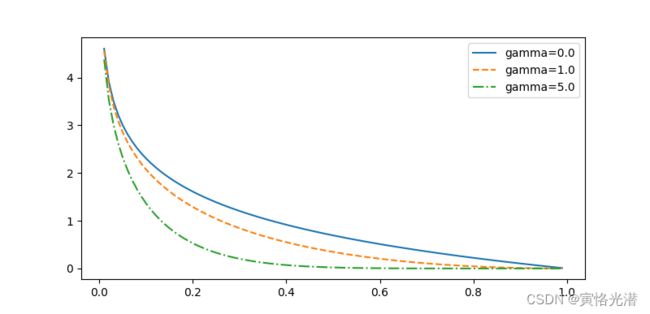
从公式可以看到,增大γ可以有效减小正类预测概率较大时的损失。同样的画图来直观的看下:
gammas = [0, 1, 5]
lines = ['-', '--', '-.']
d2l.set_figsize()
def focal_loss(gamma, x):
return -(1-x)**gamma * x.log()
x = nd.arange(0.01, 1, 0.01)
for l, gamma in zip(lines, gammas):
y = d2l.plt.plot(x.asnumpy(), focal_loss(gamma, x).asnumpy(), l, label='gamma=%.1f' % gamma)
d2l.plt.legend()
d2l.plt.show()class FocalLoss(gluon.loss.Loss):
def __init__(self, axis=-1, alpha=0.25, gamma=2, batch_axis=0, **kwargs):
super(FocalLoss, self).__init__(None, batch_axis, **kwargs)
self._axis = axis
self._alpha = alpha
self._gamma = gamma
def hybrid_forward(self, F, output, label):
output = F.softmax(output)
pj = F.pick(output, label, axis=self._axis, keepdims=True)
loss = -self._alpha * ((1 - pj) ** self._gamma) * F.log(pj)
return F.mean(loss, axis=self._batch_axis, exclude=True)其中F.pick来根据标签选取各个概率,也就是上面公式中的![]() 。返回值跟上面的SmoothL1Loss一样都是按照选定的维度求均值。这个焦点损失可以弥补上面平滑损失由于平滑而迭代慢的问题,现在我们结合这两个损失函数来训练模型。
。返回值跟上面的SmoothL1Loss一样都是按照选定的维度求均值。这个焦点损失可以弥补上面平滑损失由于平滑而迭代慢的问题,现在我们结合这两个损失函数来训练模型。
SSD改进版本
我们使用上述的改进过的两个损失函数来替换原来的,发现效果要好很多,最起码多出了很多检测框,置信度依然不是很正确,不过发现0.1的置信度有很多锚框了,于是将置信度调整为0.3,减少锚框数,我们来看下全部代码:
import d2lzh as d2l
from mxnet import gluon, image, nd, init, contrib, autograd
from mxnet.gluon import loss as gloss, nn
import time
def cls_predictor(num_anchors, num_classes):
'''
类别预测层
参数
------
通道数:num_anchors*(num_classes+1)
其中类别数需要加一个背景
卷积核大小:3,填充:1
可以保持输出的高宽不变
'''
return nn.Conv2D(num_anchors*(num_classes+1), kernel_size=3, padding=1)
def bbox_predictor(num_anchors):
'''
边界框预测层
参数
-----
通道数:num_anchors*4
为每个锚框预测4个偏移量
'''
return nn.Conv2D(num_anchors*4, kernel_size=3, padding=1)
def forward(x, block):
block.initialize()
return block(x)
Y1 = forward(nd.zeros((2, 8, 20, 20)), cls_predictor(5, 10))
Y2 = forward(nd.zeros((2, 16, 10, 10)), cls_predictor(3, 10))
def flatten_pred(pred):
return pred.transpose((0, 2, 3, 1)).flatten()
def concat_preds(preds):
return nd.concat(*[flatten_pred(p) for p in preds], dim=1)
def down_sample_blk(num_channels):
'''
高宽减半块
步幅为2的2x2的最大池化层将特征图的高宽减半
串联两个卷积层和一个最大池化层
'''
blk = nn.Sequential()
for _ in range(2):
blk.add(nn.Conv2D(num_channels, kernel_size=3, padding=1),
nn.BatchNorm(in_channels=num_channels), nn.Activation('relu'))
blk.add(nn.MaxPool2D(pool_size=(2, 2), strides=2))
return blk
def base_net():
'''
基础网络块
串联3个高宽减半块,以及通道数翻倍
'''
blk = nn.Sequential()
for n in [16, 32, 64]:
blk.add(down_sample_blk(n))
return blk
def get_blk(i):
if i == 0:
blk = base_net()
elif i == 4:
blk = nn.GlobalMaxPool2D()
else:
blk = down_sample_blk(128)
return blk
def blk_forward(X, blk, size, ratio, cls_predictor, bbox_predictor):
Y = blk(X)
anchors = contrib.nd.MultiBoxPrior(Y, sizes=size, ratios=ratio)
cls_preds = cls_predictor(Y)
bbox_preds = bbox_predictor(Y)
return (Y, anchors, cls_preds, bbox_preds)
sizes = [[0.2, 0.272], [0.37, 0.447], [0.54, 0.619], [0.71, 0.79], [0.88, 0.961]]
ratios = [[1, 2, 0.5]]*5
num_anchors = len(sizes[0])+len(ratios[0])-1
class TinySSD(nn.Block):
def __init__(self, num_classes, **kwargs):
super(TinySSD, self).__init__(**kwargs)
self.num_classes = num_classes
for i in range(5):
setattr(self, 'blk_%d' % i, get_blk(i))
setattr(self, 'cls_%d' %i, cls_predictor(num_anchors, num_classes))
setattr(self, 'bbox_%d' % i, bbox_predictor(num_anchors))
def forward(self, X):
anchors, cls_preds, bbox_preds = [None]*5, [None]*5, [None]*5
for i in range(5):
X, anchors[i], cls_preds[i], bbox_preds[i] = blk_forward(X, getattr(self, 'blk_%d' % i), sizes[i], ratios[i],
getattr(self, 'cls_%d' % i),
getattr(self, 'bbox_%d' % i))
return (nd.concat(*anchors, dim=1),
concat_preds(cls_preds).reshape(0, -1, self.num_classes+1),
concat_preds(bbox_preds))
net=TinySSD(num_classes=1)
net.initialize()
X=nd.zeros((32,3,256,256))
anchors,cls_preds,bbox_preds=net(X)
#加载皮卡丘数据集并初始化模型
batch_size=8#本人配置不行,批处理大小调小点
train_iter,_=d2l.load_data_pikachu(batch_size)
ctx,net=d2l.try_gpu(),TinySSD(num_classes=1)
net.initialize(init=init.Xavier(),ctx=ctx)
trainer=gluon.Trainer(net.collect_params(),'sgd',{'learning_rate':0.2,'wd':5e-4})
#定义损失函数
class SmoothL1Loss(gloss.Loss):
def __init__(self, batch_axis=0, **kwargs):
super(SmoothL1Loss, self).__init__(None, batch_axis, **kwargs)
def hybrid_forward(self, F, output, label, mask):
loss = F.smooth_l1((output - label) * mask, scalar=1.0)
return F.mean(loss, self._batch_axis, exclude=True)
class FocalLoss(gloss.Loss):
def __init__(self, axis=-1, alpha=0.25, gamma=2, batch_axis=0, **kwargs):
super(FocalLoss, self).__init__(None, batch_axis, **kwargs)
self._axis = axis
self._alpha = alpha
self._gamma = gamma
def hybrid_forward(self, F, output, label):
output = F.softmax(output)
pj = F.pick(output, label, axis=self._axis, keepdims=True)
loss = -self._alpha * ((1 - pj) ** self._gamma) * F.log(pj)
return F.mean(loss, axis=self._batch_axis, exclude=True)
#cls_loss = gloss.SoftmaxCrossEntropyLoss()
#bbox_loss = gloss.L1Loss()
cls_loss = FocalLoss()
bbox_loss = SmoothL1Loss()
def calc_loss(cls_preds,cls_labels,bbox_preds,bbox_labels,bbox_masks):
cls=cls_loss(cls_preds,cls_labels)
#bbox=bbox_loss(bbox_preds*bbox_masks,bbox_labels*bbox_masks)
bbox=bbox_loss(bbox_preds,bbox_labels,bbox_masks)
return cls+bbox
#评价函数
def cls_eval(cls_preds,cls_labels):
#类别预测结果放在最后一维,所以argmax需指定最后一维
return (cls_preds.argmax(axis=-1)==cls_labels).sum().asscalar()
def bbox_eval(bbox_preds,bbox_labels,bbox_masks):
return ((bbox_labels-bbox_preds)*bbox_masks).abs().sum().asscalar()
#训练模型
for epoch in range(20):
acc_sum,mae_sum,n,m=0.0,0.0,0,0
train_iter.reset()
start=time.time()
for batch in train_iter:
X=batch.data[0].as_in_context(ctx)
Y=batch.label[0].as_in_context(ctx)
with autograd.record():
#生成多尺度锚框,为每个锚框预测类别和偏移量
anchors,cls_preds,bbox_preds=net(X)
bbox_labels,bbox_masks,cls_labels=contrib.nd.MultiBoxTarget(anchors,Y,cls_preds.transpose((0,2,1)))
l=calc_loss(cls_preds,cls_labels,bbox_preds,bbox_labels,bbox_masks)
l.backward()
trainer.step(batch_size)
acc_sum+=cls_eval(cls_preds,cls_labels)
n+=cls_labels.size
mae_sum+=bbox_eval(bbox_preds,bbox_labels,bbox_masks)
m+=bbox_labels.size
if(epoch+1)%5==0:
print('迭代次数:%2d,类别损失误差:%.2e,正类锚框偏移量平均绝对误差:%.2e,耗时:%.1f秒'%(epoch+1,1-acc_sum/n,mae_sum/m,time.time()-start))
net.collect_params().save('ssd.params')
img=image.imread('pkq.png')
feature=image.imresize(img,256,256).astype('float32')
X=feature.transpose((2,0,1)).expand_dims(axis=0)#转换成卷积层需要的四维格式
#net.collect_params().load('ssd.params')
def predict(X):
anchors,cls_preds,bbox_preds=net(X.as_in_context(ctx))
cls_probs=cls_preds.softmax().transpose((0,2,1))
output=contrib.nd.MultiBoxDetection(cls_probs,bbox_preds,anchors)
idx=[i for i,row in enumerate(output[0]) if row[0].asscalar()!=-1]
return output[0,idx]
output=predict(X)
d2l.set_figsize((5,5))
def display(img,output,threshold):
fig=d2l.plt.imshow(img.asnumpy())
for row in output:
score=row[1].asscalar()
if scoreoutput[0,idx]
附带上节的一个知识点的解释
idx=[i for i,row in enumerate(output[0]) if row[0].asscalar()!=-1]
return output[0,idx]对这部分增补个解释,对于初学者可能有点不理解,output是来自MultiBoxDetection函数的返回:第一列是类别;第二列是置信度;后面的四列就是左上角与右下角的坐标(相对坐标)
if row[0].asscalar()!=-1这里就是将第一列是-1(背景或非极大值抑制中被移除)的情况筛选掉。所以返回的idx就是所有正类的行索引
return output[0,idx]输出正类的锚框
其中ids是列表,我们举个例子:
from mxnet import nd
a=a.reshape(3,4,5)
'''
[[[ 0. 1. 2. 3. 4.]
[ 5. 6. 7. 8. 9.]
[10. 11. 12. 13. 14.]
[15. 16. 17. 18. 19.]]
[[20. 21. 22. 23. 24.]
[25. 26. 27. 28. 29.]
[30. 31. 32. 33. 34.]
[35. 36. 37. 38. 39.]]
[[40. 41. 42. 43. 44.]
[45. 46. 47. 48. 49.]
[50. 51. 52. 53. 54.]
[55. 56. 57. 58. 59.]]]
'''
a[0]
'''
[[ 0. 1. 2. 3. 4.]
[ 5. 6. 7. 8. 9.]
[10. 11. 12. 13. 14.]
[15. 16. 17. 18. 19.]]
'''
a[0,[2,3]]
'''
[[10. 11. 12. 13. 14.]
[15. 16. 17. 18. 19.]]
''' 另外a[0,2,3]这样的写法等价于a[0][2][3]