机器学习 对数几率回归模型(Python实现)
本文介绍对数几率回归模型,是一个典型的二分类任务学习模型
书接上回,我们可以对一个数据集得到它的回归方程
我们是这样去解读回归方程的:在相关属性下对样例的某一特征的度量
我们根据回归方程得到的特征度量是一个连续值,我们可以根据这个度量值进行分类
例如:大学的绩点计算,当我们的绩点大于等于2.0才能拿到学位,否则拿不到学位,我们可以认为当度量值达到多少时将样例视为一类,而没达到的样例分为另一类。
但是问题就在于:1.训练数据集中需要预测的特征是分类的标签(0, 1),而不是其度量值
2.若训练集给出了需要预测的特征的分类标签(0, 1)和度量值,但是我们无法知道两个分类的度量值的界限
根据我们的需求,提出以下假设:
我们的线性方程为:![]()
设有一个函数g(x):
将我们的线性方程和这个g(x)合并可得
这样我们就可利用这个函数模型来对数据分类了
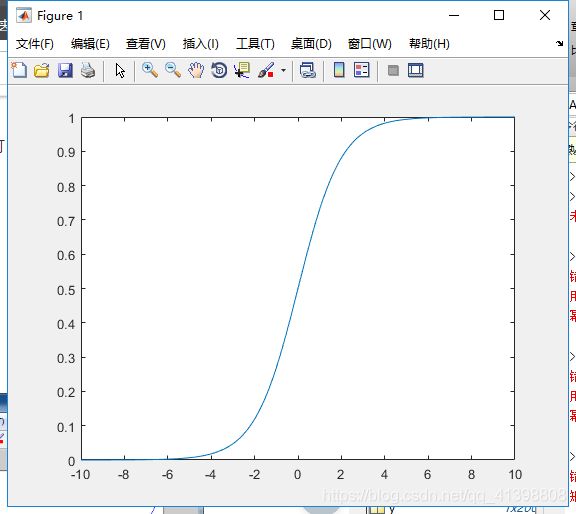
我们可以像推导线性回归函数那样,找到优化目标,从而求出使得方程最优的参数ω和b,但是函数模型是一个分段函数,不连续,无法求得统一的参数,那我们是否可以找到一个类似的连续函数,即参数在取中间值时函数变化陡峭,参数在取+∞或-∞时,函数趋近与1和0,其函数图像如下:
使用最多的就是对数几率函数,其标准形式为
当然不止是对数几率函数可以,任何具有上述性质的函数都可以使用,大家可以试着寻找其他的函数来创建模型。
我们将我们的线性回归方程与对数几率函数合并,得到我们的新模型如下:
我们依然使用差值来度量它的预测准确度,则我们的优化目标函数(代价函数)如下:
表示真实值和预测值差值的平方和,其值越小代表预测越准确。
我们可以使用梯度下降算法来计算上述优化目标。
梯度下降法公式如下(梯度下降法的证明推导过程见https://blog.csdn.net/qq_41398808/article/details/90442685):
![]()
我们的优化目标函数的一阶导数为(计算过程参考:https://www.cnblogs.com/crackpotisback/p/5545708.html):
![]()
所以我们根据该公式对参数进行迭代,就可以得到我们想要的结果:
Python实现如下:
数据集: 马疝病数据集(原数据地址:http://archive.ics.uci.edu/ml/datasets/Horse+Colic)
连续的数值型数据
一条数据实例如下(最后一项是标签,正例为1,反例为0):
2.000000 1.000000 38.500000 66.000000 28.000000 3.000000 3.000000 0.000000 2.000000 5.000000 4.000000 4.000000 0.000000 0.000000 0.000000 3.000000 5.000000 45.000000 8.400000 0.000000 0.000000 0.000000读取数据:
def loaddataset(filename):
fp = open(filename)
dataset = []
labelset = []
for i in fp.readlines():
a = i.strip().split()
#存储属性数据
dataset.append([float(j) for j in a[:len(a)-1]])
#存储标签数据
labelset.append(int(float(a[-1])))
return dataset, labelset这是两个样例的数据读取结果:
[[2.0, 1.0, 38.5, 66.0, 28.0, 3.0, 3.0, 0.0, 2.0, 5.0, 4.0, 4.0, 0.0, 0.0, 0.0, 3.0, 5.0, 45.0, 8.4, 0.0, 0.0], [1.0, 1.0, 39.2, 88.0, 20.0, 0.0, 0.0, 4.0, 1.0, 3.0, 4.0, 2.0, 0.0, 0.0, 0.0, 4.0, 2.0, 50.0, 85.0, 2.0, 2.0]]
[Finished in 3.3s][0, 0]
[Finished in 3.2s]
对数几率函数如下:
def sigmoid(z):
return 1.0 / (1 + np.exp(-z))
测试过程(先给出测试过程,是因为在训练过程中我使用测试正确率来控制迭代次数):
def test(dataset, labelset, w):
data = np.mat(dataset)
a = np.ones((len(dataset), 1))
data = np.c_[data, a]
#使用训练好的参数w进行计算
y = sigmoid(np.dot(data, w))
b, c = np.shape(y)
#记录预测正确的个数,用于计算正确率
rightcount = 0
for i in range(b):
#预测标签
flag = -1
#大于0.5的为正例
if y[i, 0] > 0.5:
flag = 1
#小于等于0.5的为反例
else:
flag = 0
#记录预测正确的个数
if labelset[i] == flag:
rightcount += 1
#正确率
rightrate = rightcount / len(dataset)
return rightrate
训练过程:
def trainning(dataset, labelset, test_data, test_label):
#将列表转化为矩阵
data = np.mat(dataset)
label = np.mat(labelset).transpose()
#初始化参数w
w = np.ones((len(dataset[0])+1, 1))
#属性矩阵最后添加一列全1列(参数w中有常数参数)
a = np.ones((len(dataset), 1))
data = np.c_[data, a]
#步长
n = 0.0001
#每次迭代计算一次正确率(在测试集上的正确率)
#达到0.75的正确率,停止迭代
rightrate = 0.0
while rightrate < 0.75:
#计算当前参数w下的预测值
c = sigmoid(np.dot(data, w))
#梯度下降的计算过程,对照着梯度下降的公式
b = c - label
change = np.dot(np.transpose(data), b)
w = w - change * n
#预测,更新正确率
rightrate = test(test_data, test_label, w)
return w最后的预测结果如下:
正确率为:0.761194
[Finished in 6.4s]
整体代码如下:
源代码和数据集资源已上传(https://download.csdn.net/download/qq_41398808/11197441)
'''
2019.05.22 19:34
马疝病数据集:连续数据,二分类,最后一列是标签列
作者:BTboay
'''
import numpy as np
def loaddataset(filename):
fp = open(filename)
dataset = []
labelset = []
for i in fp.readlines():
a = i.strip().split()
#存储属性数据
dataset.append([float(j) for j in a[:len(a)-1]])
#存储标签数据
labelset.append(int(float(a[-1])))
return dataset, labelset
def sigmoid(z):
return 1.0 / (1 + np.exp(-z))
def trainning(dataset, labelset, test_data, test_label):
#将列表转化为矩阵
data = np.mat(dataset)
label = np.mat(labelset).transpose()
#初始化参数w
w = np.ones((len(dataset[0])+1, 1))
#属性矩阵最后添加一列全1列(参数w中有常数参数)
a = np.ones((len(dataset), 1))
data = np.c_[data, a]
#步长
n = 0.0001
#每次迭代计算一次正确率(在测试集上的正确率)
#达到0.75的正确率,停止迭代
rightrate = 0.0
while rightrate < 0.75:
#计算当前参数w下的预测值
c = sigmoid(np.dot(data, w))
#梯度下降的计算过程,对照着梯度下降的公式
b = c - label
change = np.dot(np.transpose(data), b)
w = w - change * n
#预测,更新正确率
rightrate = test(test_data, test_label, w)
return w
def test(dataset, labelset, w):
data = np.mat(dataset)
a = np.ones((len(dataset), 1))
data = np.c_[data, a]
#使用训练好的参数w进行计算
y = sigmoid(np.dot(data, w))
b, c = np.shape(y)
#记录预测正确的个数,用于计算正确率
rightcount = 0
for i in range(b):
#预测标签
flag = -1
#大于0.5的为正例
if y[i, 0] > 0.5:
flag = 1
#小于等于0.5的为反例
else:
flag = 0
#记录预测正确的个数
if labelset[i] == flag:
rightcount += 1
#正确率
rightrate = rightcount / len(dataset)
return rightrate
if __name__ == '__main__':
dataset, labelset = loaddataset('horseColicTraining.txt')
test_data, test_label = loaddataset('horseColicTest.txt')
w = trainning(dataset, labelset, test_data, test_label)
rightrate = test(test_data, test_label, w)
print("正确率为:%f"%(rightrate))