西瓜书研读——第三章 线性模型：线性几率回归（逻辑回归）

西瓜书研读系列：
西瓜书研读——第三章 线性模型：一元线性回归

西瓜书研读——第三章 线性模型：多元线性回归

• 主要教材为西瓜书，结合南瓜书，统计学习方法，B站视频整理~
• 人群定位：学过高数会求偏导、线代会矩阵运算、概率论知道啥是概率
• 原理讲解，公式推导，课后习题，实践代码应有尽有，欢迎订阅

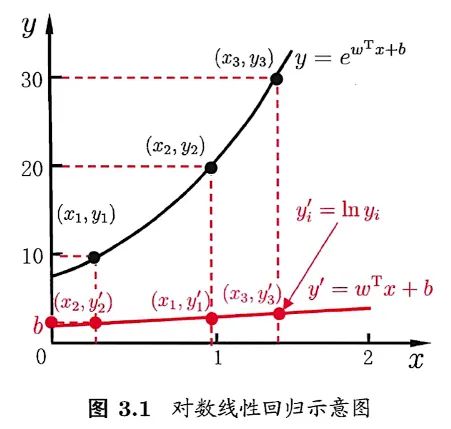
3.2.4 对数线性回归

另一方面，有时像上面这种原始的线性回归可能并不能满足需求，例如：y值并不是线性变化，而是在指数尺度上变化。这时我们可以采用线性模型来逼近y的衍生物（从一种物质到另一种划分更细的物质）

例如$lny$，这时衍生的线性模型如下所示，实际上就是相当于将指数曲线投影在一条直线上，如下图所示：

例如：$\ln y={\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b$，这就是对数线性回归，题实际上时在试图让$e^{{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b}$逼近$y$

更一般地，考虑可微函数$g(\cdot )$，其反函数为$g^{-1}$，令
$$y=g^{-1}(w^{T}x+b)\text{\hspace{1em}(3.15 )}$$
就得到了“广义的线性模型”（generalized linear model），其中，$g(\cdot )$称为联系函数（link function）。

对数函数为$g(\cdot )=ln(\cdot )$时的特例。

广义线性模型的参数估计常通过加权最小二乘法或极大似然法进行

3.3 线性几率回归

回归就是通过输入的属性值得到一个预测值，从而进行回归学习。那如何进行分类呢？

只需找一个单调可微函数将分类任务的真实标记与线性回归模型的预测值联系起来。线性几率回归正是研究这样的问题。对数几率引入了一个对数几率函数（logistic function）**,将预测值投影到0-1之间，**从而将线性回归问题转化为二分类问题。
$$\sigma (x)=\frac{1}{1+e^{-x}}$$

3.3.1 联系函数

单位阶跃函数（unit-step function）
$$y=\{\begin{array}{ll}0,& z<0;\\ & \\ 0.5,& z=0;\\ & \\ 1,& z>0;\end{array}$$

• 若预测值大于零判为正例
• 若预测值小于零判为反例
• 若预测值等于零则可任意判别

缺点是不连续性

对数几率函数（logistic function）

一定程度上近似单位阶跃函数的“替代函数”（surrogate function），并希望它单调可微

• Sigmoid函数(最为重要的代表)

  • 形似 S 的函数，它将 $z$ 值转化为一个接近 0 或 1 的 $y$ 值，并且其输出值在 $z=0$ 附近变化很陡
  • $y=\frac{1}{1+e^{-z}}$

这里确定一下Sigmoid函数是怎么来的，先补充一些知识：

---

指数族分布

指数族 (Exponential family) 分布是一类分布的总称, 该类分布的分布律（或者概率密 度函数）的一般形式如下：
$$p(y;\eta )=b(y)\exp \left({\eta }^{T}T(y)-a(\eta )\right)$$
其中， $\eta$ 称为该分布的自然参数； $T(y)$ 为充分统计量，视具体的分布而定，通常是等于随 机变量 $\mathrm{y}$ 本身； $a(\eta )$ 为配分函数； $b(y)$ 为关于随机变量 $\mathrm{y}$ 的函数，常见的伯努利分布和正态分布均属于指数族分布。

证明：伯努利分布（两点分布、0-1分布）是指数族分布，如果记成功概率为p，则失败概率为1-p，伯努利分布律为：
$$p(y)={\varphi }^y(1-\varphi {)}^{1-y}$$
其中 $y\in \{0,1\}$ ， $\varphi$ 为 y=1 的概率，即$P(y=1)=\varphi$ ， 对上式恒等变形可得：

$$\begin{array}{rl}p(y)& ={\varphi }^y(1-\varphi {)}^{1-y}\\ & =\exp \left(\ln \left({\varphi }^y(1-\varphi {)}^{1-y}\right)\right)\\ & =\exp (y\ln (\varphi )+(1-y)(1-\varphi ))\\ & =\exp \left(y(\ln \varphi -\ln (1-\varphi ))+\ln (1-\varphi )\right)\\ & =\exp \left(y\ln \left(\frac{\varphi }{1-\varphi }\right)+\ln (1-\varphi )\right)\end{array}$$
对比指数族分布的一般形式，伯努利分布的指数族分布对应参数为:
$$\begin{array}{rl}b(y)& =1\\ \eta & =\ln \left(\frac{\varphi }{1-\varphi }\right)\\ T(y)& =y\\ a(\eta )& =-\ln (1-\varphi )=\ln \left(1+e^{\eta }\right)\end{array}$$

广义线性模型的三条假设：

1. 在给定 x 的条件下，假设随机变量 y 服从某个指数族分布;
2. 在给定 x 的条件下，我们的目标是得到一个模型 h(x) 能预测出 T(y) 的期望值；
3. 假设该指数族分布中的自然参数 $\eta$ 和 $\mathbf{x}$ 呈线性关系, 即 $\eta ={\mathbf{w}}^T\mathbf{x}$

对数几率回归（逻辑回归）是对二分类问题进行建模，并假设y的取值为0、1

这样我们自然可以假设y服从伯努利分布（0 1分布），而伯努利分布是指数型的。

此时如果我们想要构建一个线性模型，就要使用广义线性模型来建模。

当然要先验证给定的x是否满足上面三条假设。

1、我们已经验证了伯努利分布是指数族分布

2、已知 y 是服从伯努利分布，而伯努利分布属于指数族分布，所以满足广义线性模型的第一 条假设，接着根据广义线性模型的第二条假设我们可以推得模型 h(x) 的表达式为：
$$h(\mathbf{x})=E[T(y\mid \mathbf{x})]$$
由于伯努利分布的 $T(y\mid \mathbf{x})=y\mid \mathbf{x}$ 所以：
$h(\mathbf{x})=E[y\mid \mathbf{x}]$ 又因为 $E[y\mid \mathbf{x}]=1\times p(y=1\mid \mathbf{x})+0\times p(y=0\mid \mathbf{x})=p(y=1\mid \mathbf{x})=\varphi$ 所以：
$$h(\mathbf{x})=\varphi$$
我们以及知道：
$$\begin{array}{c}\eta =\ln \left(\frac{\varphi }{1-\varphi }\right)\\ e^{\eta }=\frac{\varphi }{1-\varphi }\\ e^{-\eta }=\frac{1-\varphi }{\varphi }\\ e^{-\eta }=\frac{1}{\varphi }-1\\ 1+e^{-\eta }=\frac{1}{\varphi }\\ \frac{1}{1+e^{-\eta }}=\varphi \end{array}$$

将 $\varphi =\frac{1}{1+e^{-\eta }}代入h(\mathbf{x})$ 的表达式可得:

$$h(\mathbf{x})=\varphi =\frac{1}{1+e^{-\eta }}$$
这样就推出了sigmoid函数，下面就是用这个sigmoid函数进行建模了

3.3.2 对数几率回归

将 $y$ 视为样本 $\mathbf{x}$ 作为正例的可能性,则 $1-y$ 是其反例的可能性，两者的比值 $\frac{y}{1-y}$ 称为“几率”(odds)，反应了 $x$ 作为正例的相对可能性，$\ln \frac{y}{1-y}$，则称为对数几率 (log odds, 亦称logit)

根据广义模型的第三条假设，将Sigmoid函数带入到广义线性模型的表达式中， $\eta ={\mathbf{w}}^T\mathbf{x}，h(\mathbf{x})$ 最终可化为：

$$y=\frac{1}{1+e^{-({\mathbf{w}}^{\text{T}}\mathbf{x}+b)}}=p(y=1\mid \mathbf{x})$$
带入对数几率可得：

$$\ln \frac{y}{1-y}={\mathbf{w}}^{\text{T}}\mathbf{x}+b$$

优点：

1. 直接对分类可能性进行建模，无需假设数据分布，避免了假设不正确带来的问题
2. 不仅预测出类别，同时得到近似概率预测
3. 对数几率函数任意阶可导，便于求解

问题求解

如何确定 $\mathbf{w}$ 和 $b$ ？

将 $y$ 视为类后验概率估计 $p(y=1|\mathbf{x})$ (给定x的条件下，y=1的概率)

将 $\ln \frac{y}{1-y}={\mathbf{w}}^{\text{T}}\mathbf{x}+b$ 转化为 $$\ln \frac{p(y=1|\mathbf{x})}{p(y=0|\mathbf{x})}={\mathbf{w}}^{\text{T}}\mathbf{x}+b$$

• $p(y=1|\mathbf{x})=\frac{e^{{\mathbf{w}}^{\text{T}}\mathbf{x}+\mathbf{b}}}{1+e^{{\mathbf{w}}^{\text{T}}\mathbf{x}+\mathbf{b}}}$

• $p(y=0|\mathbf{x})=\frac{1}{1+e^{{\mathbf{w}}^{\text{T}}\mathbf{x}+\mathbf{b}}}$

通过“极大似然法”(maximum likelihood method，下面会讲)来估计 $\mathbf{w}$ 和 $b$

建模前还要补充几个知识

极大似然估计

比如箱子里有100个球共两种颜色，其中一种颜色有95个，现在摸出一个球是黑色，那么是黑球95个还是白球95个呢？

具体哪个多当然是不能肯定的，但我们可以知道，大概率是黑球多。

极大似然估计的目的是利用已知样本，反推最有可能导致出现这样结果的参数值是多少。

数学解释：

设总体的概率密度函数 (或分布律) 为 $f\left(y,w_1,w_2,\dots ,w_k\right),y_1,y_2,\dots ,y_m$ 为 从该总体中抽出的样本。因为 $y_1,y_2,\dots ,y_m$ 相互独立且同分布，于是，它们的联合 概率密度函数 (或联合概率) 为
$$L\left(y_1,y_2,\dots ,y_m;w_1,w_2,\dots ,w_k\right)=\prod _{i=1}^{m}f\left(y_i,w_1,w_2,\dots ,w_k\right)$$
其中, $w_1,w_2,\dots ,w_k$ 被看作固定但是末知的参数。当我们已经观测到一组样本观测值 $y_1,y_2,\dots ,y_m$ 时，要去估计末知参数，一种直观的想法就是，哪一组参数值使得现在的样本观测值出现的概率最大, 哪一组参数可能就是真正的参数，我们就用它作为参数的估计值, 这就是所谓的极大似然估计。

对率回归模型最大化“对数似然”（loglikelihood），即令每个样本属于其真实标记的概率越大越好

极大似然估计的具体方法：
通常记$L\left(y_1,y_2,\dots ,y_m;w_1,w_2,\dots ,w_k\right)=L(\mathbf{w})$ ,并称其为似然函数。于是求 $\mathbf{w}$ 的极大似然估计就归结为求 $L(\mathbf{w})$ 的最大值点。由于对数函数是单调递增函数，所以
$$\ln L(\mathbf{w})=\ln \left(\prod _{i=1}^{m}f\left(y_i,w_1,w_2,\dots ,w_k\right)\right)=\sum _{i=1}^m\ln f\left(y_i,w_1,w_2,\dots ,w_k\right)$$

与 $L(\mathbf{w})$ 有相同的最大值点, 而在许多情况下,转将累乘变成累加，更方便计算。

于是可以求 $L(\mathbf{w})$ 的对数，这样我们就将求 $L(\mathbf{w})$ 的最大值点转化为了求 $\ln L(\mathbf{w})$ 的最大值点，通常称 $\ln L(\mathbf{w})$ 为对数似然函数。

对数几率回归的极大似然估计:
已知随机变量 y 取 1 和 0 的概率分别为
$$\begin{array}{l}p(y=1\mid x)=\frac{e^{w^{\mathrm{T}}x+b}}{1+e^{w^{\mathrm{T}}x+b}}\\ p(y=0\mid x)=\frac{1}{1+e^{w^{\mathrm{T}}x+b}}\end{array}$$
令 $\beta =(w;b),\hat{x}=(x;1)$ , 则 $w^{T}x+b$ 可简写为 ${\beta }^T\hat{x}$ ,于是上式可化简为

KaTeX parse error: Unknown column alignment: p at position 16: \begin{array} p̲p(y=1 \mid x)=\…

于是，使用一个小技巧即可得到随机变量 y 的分布律表达式

$$p(y\mid \mathbf{x};\mathbf{w},b)=y\cdot p_1(\hat{\mathbf{x}};\mathbf{\beta })+(1-y)\cdot p_0(\hat{\mathbf{x}};\mathbf{\beta })\text{\hspace{1em}(3.26 )}$$
或者

$$p(y\mid \mathbf{x};\mathbf{w},b)={\left[p_1(\hat{\mathbf{x}};\mathbf{\beta })\right]}^y{\left[p_0(\hat{\mathbf{x}};\mathbf{\beta })\right]}^{1-y}$$

根据对数似然函数的定义可知

$$\ln L(\mathbf{w})=\sum _{i=1}^m\ln f\left(y_i,w_1,w_2,\dots ,w_k\right)$$
由于此时的 y为离散型, 所以将对数似然函数中的概率密度函数换成分布律即可

$$\ell (\mathbf{w},b)=\ln L(\mathbf{w},b)=\sum _{i=1}^m\ln p\left(y_i\mid {\mathbf{x}}_i;\mathbf{w},b\right)\text{\hspace{1em}(3.25)}$$
将
$$p(y\mid \mathbf{x};\mathbf{w},b)=y\cdot p_1(\hat{\mathbf{x}};\mathbf{\beta })+(1-y)\cdot p_0(\hat{\mathbf{x}};\mathbf{\beta })$$
代入对公式(3.25)数似然函数可得:
$$\ell (\mathbf{\beta })=\sum _{i=1}^m\ln \left(y_i{p}_1\left({\hat{\mathbf{x}}}_i;\mathbf{\beta }\right)+\left(1-y_i\right)p_0\left({\hat{\mathbf{x}}}_i;\mathbf{\beta }\right)\right)$$

其中$p_1({\hat{\mathbf{x}}}_i;\mathbf{\beta })=\frac{e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}}{1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}},p_0({\hat{\mathbf{x}}}_i;\mathbf{\beta })=\frac{1}{1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}}$，代入上式可得
$$\begin{array}{rl}\ell (\mathbf{\beta })& =\sum _{i=1}^m\ln \left(\frac{y_i{e}^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}+1-y_i}{1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}}\right)\\ & =\sum _{i=1}^m\left(\ln (y_i{e}^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}+1-y_i)-\ln (1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i})\right)\end{array}$$
由于$y_i$=0或1，则
$$\ell (\mathbf{\beta })=\{\begin{array}{ll}{\sum }_{i=1}^m(-\ln (1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i})),& y_i=0\\ {\sum }_{i=1}^m({\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i-\ln (1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i})),& y_i=1\end{array}$$

两式综合可得
$$\ell (\mathbf{\beta })=\sum _{i=1}^m\left(y_i{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i-\ln (1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i})\right)$$

由于此式仍为极大似然估计的似然函数，所以最大化似然函数等价于最小化似然函数的相反数，也即在似然函数前添加负号即可得公式(3.27)。

值得一提的是，若将公式(3.26)这个似然项改写为
$$p(y_i|{\mathbf{x}}_i;\mathbf{w},b)=[p_1({\hat{\mathbf{x}}}_i;\mathbf{\beta }){]}^{y_i}[p_0({\hat{\mathbf{x}}}_i;\mathbf{\beta }){]}^{1-y_i}$$
再将其代入公式(3.25)可得
$$\begin{array}{rl}\ell (\mathbf{\beta })& =\sum _{i=1}^m\ln \left([p_1({\hat{\mathbf{x}}}_i;\mathbf{\beta }){]}^{y_i}[p_0({\hat{\mathbf{x}}}_i;\mathbf{\beta }){]}^{1-y_i}\right)\\ & =\sum _{i=1}^m\left[y_i\ln \left(p_1({\hat{\mathbf{x}}}_i;\mathbf{\beta })\right)+(1-y_i)\ln \left(p_0({\hat{\mathbf{x}}}_i;\mathbf{\beta })\right)\right]\\ & =\sum _{i=1}^m\left\{y_i\left[\ln \left(p_1({\hat{\mathbf{x}}}_i;\mathbf{\beta })\right)-\ln \left(p_0({\hat{\mathbf{x}}}_i;\mathbf{\beta })\right)\right]+\ln \left(p_0({\hat{\mathbf{x}}}_i;\mathbf{\beta })\right)\right\}\\ & =\sum _{i=1}^m\left[y_i\ln \left(\frac{p_1({\hat{\mathbf{x}}}_i;\mathbf{\beta })}{p_0({\hat{\mathbf{x}}}_i;\mathbf{\beta })}\right)+\ln \left(p_0({\hat{\mathbf{x}}}_i;\mathbf{\beta })\right)\right]\\ & =\sum _{i=1}^m\left[y_i\ln \left(e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}\right)+\ln \left(\frac{1}{1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}}\right)\right]\\ & =\sum _{i=1}^m\left(y_i{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i-\ln (1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i})\right)\end{array}$$

显然，此种方式更易推导出公式(3.27)

$$\ell (\mathbf{\beta })=\sum _{i=1}^m(-y_i{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i+\ln (1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}))\text{\hspace{1em}(3.27)}$$

用另一种思路来推：

知识补充：

信息论

上式是关于$\beta$的高阶可导连续凸函数，可以用梯度下降法、牛顿法等求其最优解。

点击查看梯度下降法

• 代码实践部分将发布于公众号 小白白学技术

• 获取多资料 关注公众号 小白白学技术