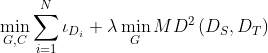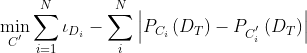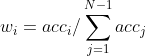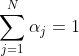M3SDA：用于多源域自适应的矩匹配

1、收集并注释了迄今为止最大的UDA数据集DomainNet，该数据集包含六个域和大约60万个图像，分布在345个类别中，解决了多源UDA研究的数据可用性差距。

2、提出了一种新的深度学习方法，多源域自适应矩匹配（M3SDA），旨在通过动态对齐特征分布的矩，将从多个标记源域学习的知识迁移到未标记目标域。

3、为单信源域和多信源域自适应中的矩匹配方法提供了新的理论见解。并通过实验证明我们的新数据集在基准测试最先进的多源领域自适应方法方面的能力，以及我们提出的模型的优势。

DomainNet数据集

1、DomainNet数据集 

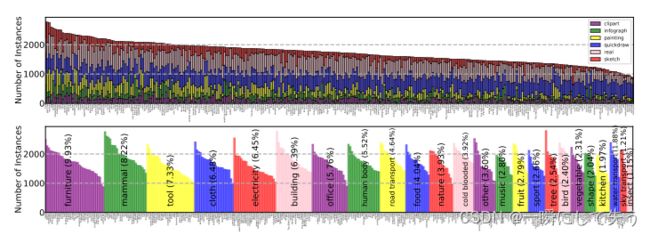
       我们提出的数据集包含约60万幅图像，分布在345个类别和6个不同的域中。我们获取到各种物体分割，从家具、布料、电子到哺乳动物、建筑等。

6个域包括剪贴画（clp）；信息图（inf）；绘画（pnt）；Quickdraw（qdr）；照片（rel）；草图（skt）。

       为了控制注释质量，我们为每个图像指定了两个注释器，并且只拍摄两个注释器都同意的图像。在过滤过程之后，我们从120万张网络抓取的图像中保留了423.5k张图像。

a、对于剪贴画和信息图领域，该数据集平均每个类别约有150个图像；

b、对于绘画和草图领域，每个类别约有220个图像；

c、对于真实领域，每个类别约有510个图像。

上图显示DomainNet数据集的统计数据。这两个图显示了按实例总数排序的对象类。上图显示了每个域在数据集中所占的百分比；下图显示了由24个不同分区分组的实例数。

2、理论基础

2.1单源域的UDA（无标签域适应）

          在过去几十年中，人们提出了各种单源UDA方法。这些方法在分类上可分为三类。

a、基于差异的DA方法。它利用不同的度量学习模式来减少源域和目标域之间的域迁移（MMD、KL散度、H散度）。

b、基于对抗的方法。利用域鉴别器通过对抗目标来鼓励域混淆。生成对抗网络广泛用于学习域不变特征以及生成虚假源域或目标数据。

c、基于重构的。利用数据重构帮助DA模型学习域不变特征（dualGAN、cycle GAN、disco GAN、CyCADA）。

       虽然这些方法在UDA方面取得了进展，但很少考虑从多个源域收集训练数据的实际情况。我们提出了一个模型来解决多源域自适应问题。

2.2多源域自适应

多源域自适应假设来自多个源域的训练数据可用，即MSDA。

a、H∆H散度——源域和目标域加权组合之间的散度。

b、通过最小化最近k源域的经验损失，建立了模型预期损失的一般界限。

c、目标假设可以由源域假设的加权组合来表示。

d、交叉熵损失理论保证的归一化解。

本论文的模型通过匹配矩直接匹配所有的数据分布。

2.3矩匹配

为了减少域差异，在两个域之间提出了不同的矩匹配方案。

a、MMD匹配。

b、匹配二阶矩的方法。

c、在RKHS中对齐内维协方差矩阵。

d、引入了矩匹配正则化器来匹配高阶矩。

e、基于生成对抗网络的矩匹配方法。（GMMN、MMD-GAN）

与这些方法相比，本论文是匹配多个域的分布矩。

3、多源域适应的矩匹配 

标签源域集合：标记源域的集合；

无标签目标域：；

多源域自适应问题——在给定假设空间H中找到一个假设，从而最小化上的测试目标误差。

定义1：假设 分别是来自 域的样本集合，然后和之间的矩距离为：

M3SDA框架

 M3SDA模型由特征提取器G、矩匹配组件和一组N个分类器组成。

特征提取器G——DS、DT映射到公共潜在特征空间；

矩匹配组件——最小化矩相关距离；

N个分类器——在具有交叉熵损失的注释源域上训练。

因此，总体目标损失函数为：

——域上分类器的softmax交叉熵损失；

λ——控制参数。

假设在对齐p（x）时，p（y | x）将自动对齐，我们进一步提出了M3SDA-β。

M3SDA-β

我们利用每个域的两个分类器来形成N对分类器。

训练过程包括三个步骤：

i） 训练G和来正确分类多源域样本,如上面总体目标损失函数所示。

ii）针对固定G训练分类器对，使每对分类器在目标域上的差异尽可能大。

PS：我们将两个分类器的差异定义为两个分类器输出之间的L1距离。

因此，目标函数为：

、分别表示、在目标域上的输出。

iii）固定并训练G，以最小化目标域上每个分类器对的差异。

目标函数为：

集成模式

在测试阶段，来自目标域的测试数据通过特征生成器和N个分类器进行迁移。通过下面两种模式来组合分类器的输出：

a、平均分类器的输出，标记为

b、导出权重向量（，假设第N个域是目标域）。最终的预测是输出的加权平均值。

权重向量的主要原理是使其表示目标域和源域之间的内在紧密性。加权向量由第i个域和第N个域之间的纯信源域精度导出，即。

4、原理解析 

        介绍了一个严格的多源域自适应二值分类模型。一个域D=（µ，f）由输入空间X上的概率测度（分布）µ和标记函数f:X→ {0, 1}构成。

假设是一个函数h:X→ {0, 1}.。在域分布µ下，h与域标记函数f不一致的概率定义为：

对于源域和目标域，我们将假设h的源域误差和目标域误差称为和。

对于经验分布，我们用表示相应的经验误差，例如和。

a、给定权重向量，;

b、将假设h的α加权信源域误差定义为。

PS：。α加权信源域的经验误差可以类似地定义，并用表示。

定理1：

       假设条件：1、H为VC维度的假设空间；

                         2、m为来自所有源域标记样本的大小；

                         3、为从中提取的大小为（）的标记样本集，并由真 实标记函数进行标记。

定理阐述：如果是的经验极小值，对于固定权重向量α和是目标域误差最小值，那么对于任何δ∈ （0，1）和任何，存在N个整数和N常数,此时概率至少为1− δ

其中：

;

;

定理1表明，假设学习的目标误差上界取决于目标域和每个源域之间的成对矩散度。此外很明显，界限的最后一项是源域之间的成对散度下界。

ps:要看到这一点，需要注意示例由两个源域、和目标域组成，因为是一个度量.规定下限的三角不等式如下：

这促使我们的算法也对齐每对源域之间的矩。如果源域本身没有对齐，则不可能将目标域与每个源域完全对齐。

5、总结 

1、收集、注释和评估了迄今为止最大的领域适应数据集DomainNet。由于存在显著的领域差距和大量类别，该数据集具有挑战性。

2、提出了M3SDA，将多个源域与目标域对齐。在交叉矩散度的框架下，推导了该方法有意义的误差界。

3、将矩匹配组件引入深度神经网络，并以端到端的方式训练模型。