NNDL 作业12:第七章课后题
文章目录
-
- 习题7-1 在小批量梯度下降中,试分析为什么学习率要和批量大小成正比
- 习题7-2 在Adam算法中,说明指数加权平均的偏差修正的合理性(即公式(7.27)和公式(7.28).
- 习题7-9 证明在标准的随机梯度下降中,权重衰减正则化和L2正则化的效果相同.并分析这一结论在动量法和Adam算法中是否依然成立
- 全面总结网络优化
- 总结
- 参考
习题7-1 在小批量梯度下降中,试分析为什么学习率要和批量大小成正比
在小批量梯度下降中:
g t ( θ ) = 1 K ∑ ( x , y ) ∈ S t ∂ L ( y , f ( x ; θ ) ) ∂ θ g_t(\theta)=\frac{1}{K}\sum_{(x,y)\in S_t}^{}\frac{\partial L(y,f(x;\theta))}{\partial \theta} gt(θ)=K1(x,y)∈St∑∂θ∂L(y,f(x;θ))
θ t = θ t − 1 − α g t \theta_t=\theta_{t-1}-\alpha g_t θt=θt−1−αgt
令 g t = 1 K δ g_t = \frac{1}{K}\delta gt=K1δ,则: θ t = θ t − 1 − α K δ \theta_t = \theta_{t-1}-\frac{\alpha}{K}\delta θt=θt−1−Kαδ
因此我们要使得参数最优,则 α K \frac{\alpha}{K} Kα为最优的时候的常数,故学习率要和批量大小成正比。
批量大小越大,随机梯度的方差越小,引入的噪声也越小,训练也越稳定,因此可以设置较大的学习率;反之亦然,所以在小批量梯度下降中,学习率要和批量大小成正比。
习题7-2 在Adam算法中,说明指数加权平均的偏差修正的合理性(即公式(7.27)和公式(7.28).
公式7.27: M ^ t = M t 1 − β 1 t \hat{M}_t=\frac{M_t}{1-\beta_1^t} M^t=1−β1tMt
公式7.28: G ^ t = G t 1 − β 2 t \hat{G}_t=\frac{G_t}{1-\beta_2^t} G^t=1−β2tGt
在Adam算法中:
M t = β 1 M t − 1 + ( 1 − β 1 ) g t M_t = \beta_1 M_{t-1}+(1-\beta_1)g_t Mt=β1Mt−1+(1−β1)gt
G t = β 2 G t − 1 + ( 1 − β 2 ) ⊙ g t G_t = \beta_2 G_{t-1} + (1-\beta_2)\odot g_t Gt=β2Gt−1+(1−β2)⊙gt
因此当 β 1 → 1 \beta_1\rightarrow 1 β1→1, β 2 → 1 \beta_2 \rightarrow 1 β2→1的时候:
lim β 1 → 1 M t = M t − 1 \lim_{\beta_1\rightarrow 1} M_t = M_{t-1} β1→1limMt=Mt−1
lim β 2 → 1 G t = G t − 1 \lim_{\beta_2\rightarrow 1} G_t = G_{t-1} β2→1limGt=Gt−1
因此可以发现此时梯度消失,因此需要进行偏差修正。
习题7-9 证明在标准的随机梯度下降中,权重衰减正则化和L2正则化的效果相同.并分析这一结论在动量法和Adam算法中是否依然成立
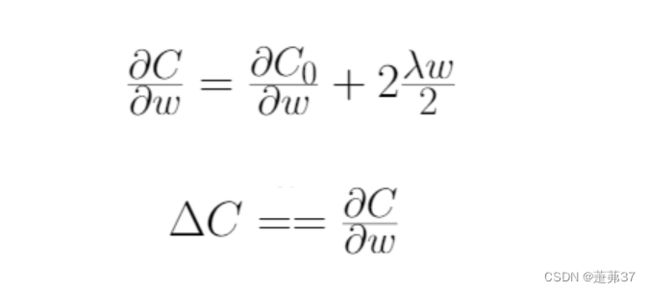
得到损失函数的偏导数结果后,将结果代入梯度下降学习规则中,代入后,打开括号,重新排列,使其等价于在一定假设下的权值衰减方程。
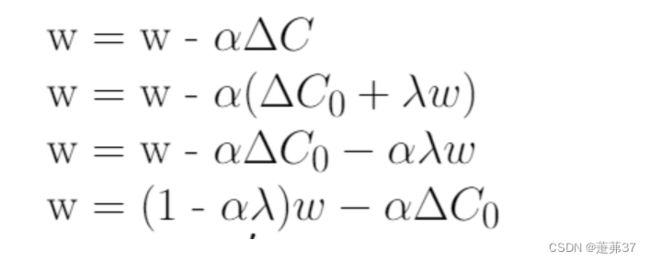
最终重新排列的L2正则化方程和权值衰减方程之间的唯一区别是α(学习率)乘以λ(正则化项)。为了得到两个方程,我们用λ来重新参数化L2正则化方程。
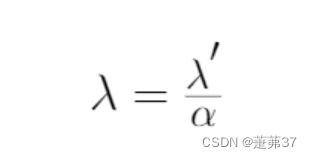
将λ’替换为λ,对L2正则化方程进行重新参数化,将其等价于权值衰减方程,如下式所示。
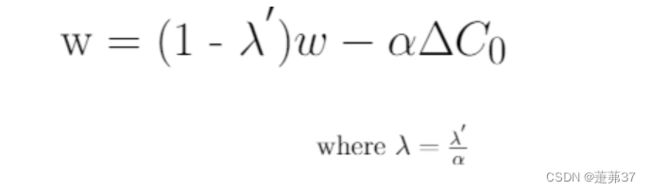
综上,在标准的随机梯度下降中,权重衰减正则化和l2正则化的效果相同得证。
但这一结论在动量法和Adam算法中不成立。
L2正则化梯度更新的方向取决于最近一段时间内梯度的加权平均值。
当与自适应梯度相结合时(动量法和Adam算法),L2正则化导致具有较大历史参数 (和/或) 梯度振幅的权重被正则化的程度小于使用权值衰减时的情况。
全面总结网络优化
总结
本学期最后一个作业了,整个学期学感觉收获很多。每次实验的坚持都增强了自己的自学能力和动手能力,也画了很多的思维导图,发现它真的是一个很好的复习总结的工具,能明晰知识结构体系。在以后的学习生活中可以继续使用下去。
参考
NNDL 作业12:第七章课后题_HBU_David的博客-CSDN博客
在ICLR 2019上作为会议论文发表—解耦权衰减正则化
神经网络与深度学习[邱锡鹏] 第七章习题解析