作业4：第四章课后习题

目录

习题4-2

试设计一个前馈神经网络来解决 XOR 问题，要求该前馈神经网络具有两个隐藏神经元和一个输出神经元，并使用 ReLU 作为激活函数。

习题4-3

试举例说明“死亡ReLU问题”，并提出解决方法.

习题4-7

为什么在神经网络模型的结构化风险函数中不对偏置b进行正则化?

习题 4-8

为什么在用反向传播算法进行参数学习时要采用随机参数初始化的方式而不是直接令 w= 0, = 0？

习题4-9

梯度消失问题是否可以通过增加学习率来缓解？

参考

---

习题4-2

试设计一个前馈神经网络来解决 XOR 问题，要求该前馈神经网络具有两个隐藏神经元和一个输出神经元，并使用 ReLU 作为激活函数。

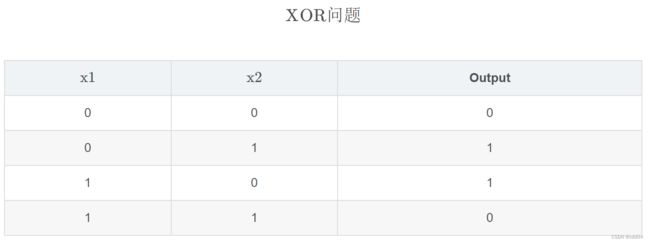
XOR问题：即异或问题，可以看成单位正方形的四个角，输入模式为(0,0),(0,1),(1,1),(1,0)。

输入模式（0,0）和（1,1）是单位正方形的两个相对的角，但它们产生相同的结果是0。另一方面，输入模式（0,1）和（1,0）是单位正方形另一对相对的角，但是它们属于类1。很显然，无法找出一条直线作为决策边界可以使（0,0）和（1,1）在一个区域，而（1,0）和（0,1）在另一个区域。

XOR输入为2个神经元，输出为一个神经元，此题要求隐藏神经元为2个，故只要两层全连接层即可

• 数据集：输入为两位二进制，共四种情况，输出为一个二进制表示的数，要么为0，要么为1
• 网络模型：用pytorch搭建两层全连接层神经网络
• 训练：计算网络输出，计算损失函数，反向传播，参数更新
• 求权重和偏置

import torch.nn as nn
import torch
import torch.optim as optim

# 异或门模块由两个全连接层构成
class XORModule(nn.Module):
    def __init__(self):
        super(XORModule, self).__init__()
        self.fc1 = nn.Linear(2, 2)
        self.fc2 = nn.Linear(2, 1)
        self.relu = nn.ReLU()

    def forward(self, x):
        x = x.view(-1, 2)
        x = self.relu((self.fc1(x)))
        x = self.fc2(x)
        return x

# 输入和输出数据
input_x = torch.Tensor([[0, 0], [0, 1], [1, 0], [1, 1]])
input_x1 = input_x.float()
real_y = torch.Tensor([[0], [1], [1], [0]])
real_y1 = real_y.float()

# 设置损失函数和参数优化函数
net = XORModule()
loss_function = nn.MSELoss(reduction='mean')  # 用交叉熵损失函数会出现维度错误
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)  # 用Adam优化参数选不好会出现计算值超出0-1的范围

# 进行训练
for epoch in range(10000):
    out_y = net(input_x1)
    loss = loss_function(out_y, real_y1)  # 计算损失函数
    optimizer.zero_grad()  # 对梯度清零，避免造成累加
    loss.backward()  # 反向传播
    optimizer.step()  # 参数更新

# 打印计算的权值和偏置
print('w1 = ', net.fc1.weight.detach().numpy())
print('b1 = ', net.fc1.bias.detach().numpy())
print('w2 = ', net.fc2.weight.detach().numpy())
print('b2 = ', net.fc2.bias.detach().numpy())
input_test = input_x1
out_test = net(input_test)
print('input_x', input_test.detach().numpy())
print('out_y', out_test.detach().numpy())

习题4-3

试举例说明“死亡ReLU问题”，并提出解决方法.

神经网络权重更新的公式：

其中η表示学习率，Δw表示通过求导得到的当前参数的梯度（一般为正值）当学习率过大时，会导致 ηΔw 这一项很大，当 ηΔw 大于w时，更新后的w’就会变为负值；

当权重参数变为负值时，输入网络的正值会和权重相乘后也会变为负值，负值通过relu后就会输出0；如果w在后期有机会被更新为正值也不会出现大问题，但是当relu函数输出值为0时，relu的导数也为0，因此会导致后边Δw一直为0，进而导致w一直不会被更新，因此会导致这个神经元永久性死亡（一直输出0）
解决方法：

1.减小学习率

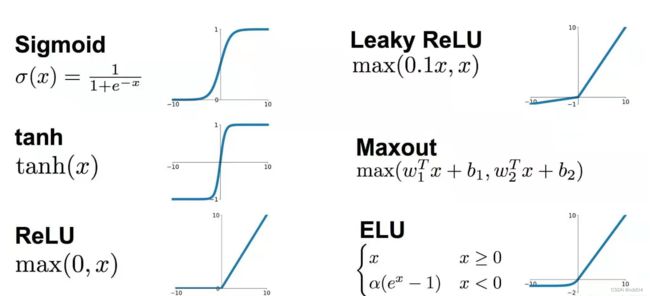
2.使用ELU、PReLU、LeakyRelu等激活函数代替 Relu

ELU、PReLU、LeakyRelu都是让Relu在自变量小于0时函数值也是一个小于0的值，从而让w小于令0在后期有机会更新为正值。

 

习题4-7

为什么在神经网络模型的结构化风险函数中不对偏置b进行正则化?

正则化的作用是为了限制模型的复杂度避免模型过拟合，提高模型的泛化能力。
对于某个神经元的输入来说，input = w(0)x(0) + w(1)x(1) + w(2)x(2) + ······ + b
对于样本特征向量X，其对input的贡献只与权重向量W有关。
若W向量中的值都很大，若特征向量X中的值发生细微的变化会导致input值的突变。
这就导致了模型的不稳定，所有我们希望得到较小的权重值。而偏置b对于所有输入样本来说都是一致的，是一个不变量，所以不需要考虑对B进行正则化。

习题 4-8

为什么在用反向传播算法进行参数学习时要采用随机参数初始化的方式而不是直接令 w= 0, = 0？

反向传播就是要将神经网络的输出误差，一级一级地传播到输入。在计算过程中，计算每一个w 对总的损失函数的影响，即损失函数对每个w的偏导。根据w的误差的影响，再乘以步长，就可以更新整个神经网络的权重。当一次反向传播完成之后，网络的参数模型就可以得到更新。更新一轮之后，接着输入下一个样本，算出误差后又可以更新一轮，再输入一个样本，又来更新一轮，通过不断地输入新的样本迭代地更新模型参数，就可以缩小计算值与真实值之间的误差，最终完成神经网络的训练。当直接令w =0，b=0时，那么第一次计算时，隐层神经元的计算结果都一样，并且在反向传播时参数更新也一样，导致在每两层之间的参数都是一样的，这样相当于隐层只有 1 个神经元。

习题4-9

梯度消失问题是否可以通过增加学习率来缓解？

在神经网络中，当前面隐藏层的学习速率低于后面隐藏层的学习速率，即随着隐藏层数目的增加，分类准确率反而下降了。这种现象叫做消失的梯度问题。

梯度消失问题是由于激活函数为类似于sigmoid与tanh，其值太大或太小时导数都趋于0；并且在深层神经网络中，误差反向传播时，传播到前几层时梯度信息也会很小。问题是可否通过增大学习率来增大梯度，以至于梯度信息可以在更新时变大。

答案是不行，增大学习率带来的缺陷会比梯度消失问题更加严重，学习率变大时，很容易使得参数跳过最优值点，然后梯度方向改变，导致参数优化时无法收敛。

参考

(1条消息) ML--XOR问题_V_lq6h的博客-CSDN博客

深度学习中梯度消失原因、梯度爆炸及解决方案