机器学习 第11章 特征选择与稀疏学习 概念总结与简单实践
一 解决的问题
跟第10章降维的思想相同,特征选择目的也是想减少用于计算的特征,尽可能从最少的特征得到准确的结果。
不过同降维不同的是,特征选择更关注特征本身是否有用,思路是只选取与问题求解有益的特征进行建模。由此,将特征划分为 相关特征、无关特征、冗余特征。
那么定义特征是否有用的标准是什么呢?
可以借助于第8章的多样性度量进行比较,把Class的label作为一种划分,把属性的切分作为一种划分,那么我们可以对这两种划分进行比较,考察两者的相关性,不合度等指标,就可以知道这个属性是否跟目标划分产生影响。
常见的特征选择大致分为三类:
过滤式:先进行特征工程,选取好的特征,然后进行训练;
包裹式:选取特征的时候就把学习器的性能作为指标,选取的特征跟学习器具有很好匹配度,更准确,但也更耗计算开销;
嵌入式:嵌入式会与L1正则化项结合起来作为Loss函数进行训练,而L1正则化更易获得稀疏解,得到更好的线性可分性质。 而模型训练结束,稀疏解也同时得到,这样也得到了仅采用一部分初始特征的模型。
既然稀疏表达有更好的线性可分性质,那么能否通过转化将数据集变成可稀疏表达的矩阵呢?由此引入字典学习,字典学习目标在于找到合适的字典,即合适的属性定义,让样本在字典属性上的表达成为稀疏表达,之后再进行下一步的求解。
反过来,也可以利用稀疏表达进行原数据的追踪。从有限的不全的信息中根据稀疏处理的方式获得准确的原始信息,这就是压缩感知解决的问题。
二 概念总结
三 习题
习题11.1 基于Relief算法,考察西瓜数据集3.0的运行结果。
数据集:西瓜集3.0
import pandas as pd
data = pd.read_csv('./CH4-TABLE4-3.csv')
import numpy as np
data1 = data[['色泽','根蒂','敲声','纹理','脐部','触感','密度','含糖率','好坏']]
data2 = data1.replace(['青绿','蜷缩','浊响','清晰','凹陷','硬滑','乌黑','稍蜷','沉闷','稍糊','稍凹','软粘','浅白','硬挺','清脆','模糊','平坦','好瓜','坏瓜'],[1,1,1,1,1,1,2,2,2,2,2,2,3,3,3,3,3,1,0])
X =np.array(data2.iloc[:,0:9])
# ---- 开始算法定义----------
# 距离采用L2范数
def L2length(a,b):
return np.linalg.norm(a-b)
# 找到最近邻距离的样本
def findNearestV(a,A):
nearest = float('inf')
sample = a
for i in A:
length = L2length(a,i)
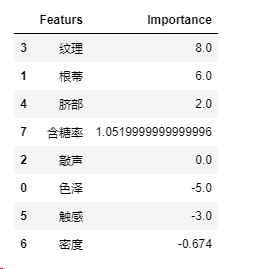
if length本来只想调用个section的函数,然后发现sklearn似乎没有这个特征评估方法。。。。下面是返回的属性相关统计量如下,index是原始数据属性的列数。
得到最相关的属性依次是纹理,根蒂和脐部。